平衡二叉树(AVL)

性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

 

　　定义：平衡二叉树或为空树,或为如下性质的二叉排序树:

  　　（1）左右子树深度之差的绝对值不超过1;

  　　（2）左右子树仍然为平衡二叉树.

      　平衡因子BF=左子树深度－右子树深度.

　　　平衡二叉树每个结点的平衡因子只能是1，0，-1。若其绝对值超过1，则该二叉排序树就是不平衡的。

 　　 如图所示为平衡树和非平衡树示意图：

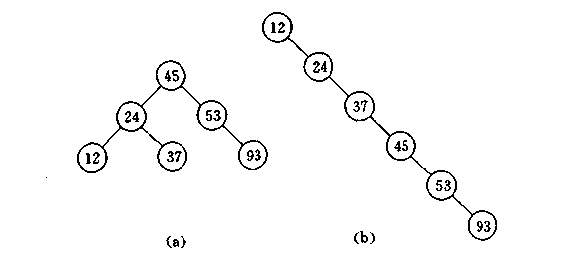
　　平衡二叉树算法思想：

 　　　　若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。　　

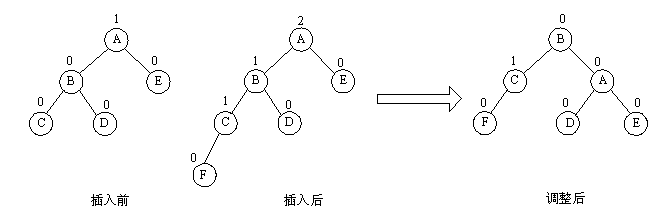
　　　　（1）LL型平衡旋转法

 

　　　　　　由于在A的左孩子B的左子树上插入结点F，使A的平衡因子由1增至2而失去平衡。故需进行一次顺时针旋转操作。 即将A的左孩子B向右上旋转代替A作为根结点，A向右下旋转成为B的右子树的根结点。而原来B的右子树则变成A的左子树。

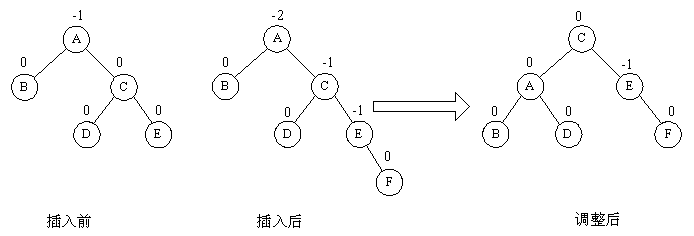
　　　　（2）RR型平衡旋转法

　　　　　　由于在A的右孩子C 的右子树上插入结点F，使A的平衡因子由-1减至-2而失去平衡。故需进行一次逆时针旋转操作。即将A的右孩子C向左上旋转代替A作为根结点，A向左下旋转成为C的左子树的根结点。而原来C的左子树则变成A的右子树。

　　　　（3）LR型平衡旋转法

　　　　　　由于在A的左孩子B的右子数上插入结点F，使A的平衡因子由1增至2而失去平衡。故需进行两次旋转操作（先逆时针，后顺时针）。即先将A结点的左孩子B的右子树的根结点D向左上旋转提升到B结点的位置，然后再把该D结点向右上旋转提升到A结点的位置。即先使之成为LL型，再按LL型处理。

 

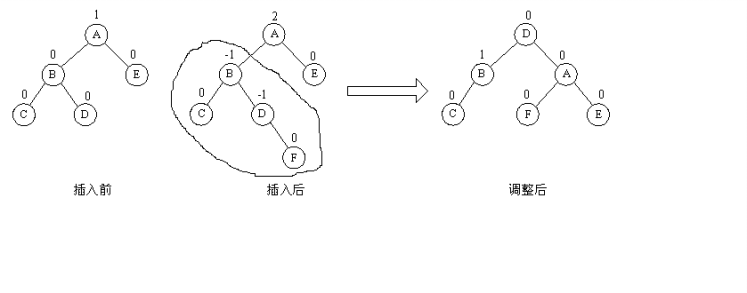
 　　　　　　如图中所示，即先将圆圈部分先调整为平衡树，然后将其以根结点接到A的左子树上，此时成为LL型，再按LL型处理成平衡型。

 

　　　　（4）RL型平衡旋转法  

 

　　　　　　　由于在A的右孩子C的左子树上插入结点F，使A的平衡因子由-1减至-2而失去平衡。故需进行两次旋转操作（先顺时针，后逆时针），即先将A结点的右孩子C的左子树的根结点D向右上旋转提升到C结点的位置，然后再把该D结点向左上旋转提升到A结点的位置。即先使之成为RR型，再按RR型处理。

 

 

 

 

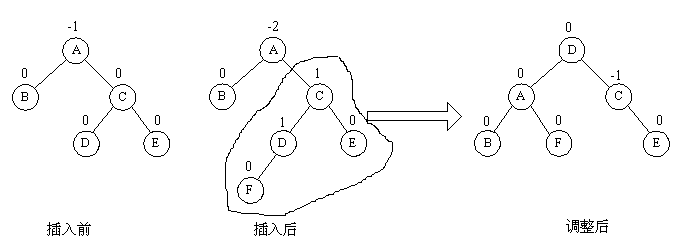
 　　　　　　如图中所示，即先将圆圈部分先调整为平衡树，然后将其以根结点接到A的左子树上，此时成为RR型，再按RR型处理成平衡型。

　　总结：如果从空树开始建立，并时刻保持平衡，那么不平衡只会发生在插入删除操作上，而不平衡的标志就是出现bf == 2或者 bf == -2的节点。