$$ %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Self-defined math definitions %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Math symbol commands \newcommand{\intd}{\,{\rm d}} % Symbol 'd' used in integration, such as 'dx' \newcommand{\diff}{{\rm d}} % Symbol 'd' used in differentiation ... $$

软件工程结对编程作业——众人齐心

项目 内容
班级：北航2020春软件工程 006班（罗杰、任健 周五） 博客园班级博客
作业：设计程序求几何对象的交点集合，支持命令行和GUI 结对项目作业
个人课程目标 提高结对编程水平，系统学习软件工程，训练软件开发能力
这个作业在哪个具体方面帮助我实现目标 实践结对编程等敏捷开发方法，学习dll相关技术
项目地址 https://github.com/prime21/IntersectProject
声明 本文标题中带有*号的章节均为和结对伙伴共享内容。 其余独立内容不存在雷同。

本作业涉及到的小组及其成员：

学号 cnblog profile
17373260（本文作者） Prime21
17373015（结对队友）
17373287
17373331（合作测试edge case伙伴） MisTariano
17231145（合作测试strong case伙伴） FuturexGO

合作测试项目:https://github.com/BUAA-SE/extremely-weak-GeoGebra

目录

(目录中标记了share的为与结对伙伴合作书写内容)

  • 个人PSP估计
  • 利用Information Hiding，Interface Design，Loose Coupling方法实现的接口设计
    • Information Hiding
    • Interface Design
    • Loose Coupling
  • 计算模块接口的设计与实现过程
    • 松耦合组件设计
    • 核心封装
  • UML图阐述实体关系
  • 计算模块接口部分的性能改进。
  • 学习Design by Contract，Code Contract 两种方法
    • 优缺点对比
    • 我们的实践
  • 计算模块部分的单元测试
    • 测试思路
    • 测试覆盖率
  • 计算模块部分异常处理说明
    • 异常设计
    • 异常测试
  • 界面模块与计算模块的对接
  • 描述结对的过程
  • 结对编程
    • 结对编程的优点缺点
    • 队友的十个优点和一个缺点
  • PSP表格登记

1 PSP 反思

PSP2.1 预估耗时（分钟） 实际耗时（分钟）
Planning 45 60
· Estimate 30 30
Development 1020 1200
· Analysis 90 120
· Design Spec 60 60
· Design Review 30 20
· Coding Standard 40 50
Design 120 120
· Coding 300 280
· Code Review 60 120
· Test 300 420
Reporting 50 20
· Test Report 20 50
· Size Measurement 10 10
· Postmortem & Process Improvement Plan 20 30
*In Total 2195 2590
  • 共性问题挖掘
    • 在设计多种直线的时候我们考虑到了直线的共性挖掘：
      • 传统的设计思路为：判断所在直线的非平行、平行与共线。非平行与平行（共线）的判定标准为交点分母是否为0，即交点是否为无穷数。平行与共线的区分可以通过计算“对角向量”的叉积，判断“对角向量”是否共线实现。（×）这是极其不可取的
      • 所以我考虑到了挖掘共性，把问题归约成直线相交和点在线上
  • 回顾：浮点数double类型的精度问题难以解决。我们和很多同学进行了比较函数-测试-确认bug-再调整比较函数的测试方式，多次回归
void getLineInter(Line a, Line b, vector<Point>& ret) {
	Point delta = b.u - a.u;
	double crs = a.v ^ b.v;
	double t1 = (delta ^ b.v) / crs;
	double t2 = (delta ^ a.v) / crs;
	if (a.online(t1) && b.online(t2)) {
		ret.push_back(a.u + a.v * t1);
	}
}
void getCirInter(Circle a, Circle b, vector<Point>& ret) {
	double dis2 = sqr(a.c.x - b.c.x) + sqr(a.c.y - b.c.y);
	if (dis2 > sqr(a.r + b.r)) return;
	if (dis2 < sqr(a.r - b.r)) return;

	double alpha = dis2 + sqr(a.r) - sqr(b.r);
	alpha /= 2 * sqrt(dis2);

	double h = sqrt(sqr(a.r) - sqr(alpha));

	Point o1o2 = Point(b.c) - Point(a.c);
	o1o2 = o1o2 / o1o2.length();

	Point vert = Point(o1o2.y, -o1o2.x);
	Point P = a.c + o1o2 * alpha;
	Point Q = P + vert * h;
	ret.push_back(Q);
	Q = P - vert * h;
	ret.push_back(Q);
}
void getLcInter(Line a, Circle b, vector<Point>& ret) {
	Point lc = a.u - b.c;
	double A = a.v.length2();
	double B = (lc * a.v) * 2;
	double C = lc.length2() - sqr(b.r);
	double delta = sqr(B) - 4 * A * C;
	if (delta >= 0) {
		delta = sqrt(delta);
		double x1 = (delta - B) / (2 * A);
		double x2 = (-delta - B) / (2 * A);

		if (a.online(x1)) ret.push_back(a.u + a.v * x1);
		if (a.online(x2)) ret.push_back(a.u + a.v * x2);
	}
}

2 设计思想

Information Hiding

Information Hiding是一个重要的程序设计思想：将不同模块的程序内部数据尽可能向外界隐藏，只在定义良好的接口处向外界展示必要的数据和函数入口。这样可以避免很多意外如：

  • 程序员意外修改核心数据
  • 程序员混淆接口实现
  • 产生大量副作用未知的调用

最后我们的解决思路是，仅仅提供没有副作用的方式。

Interface Design （接口设计）

接口设计，即实现信息隐藏以及程序结构化的重要方法，需要严格遵循信息隐藏原则，进行接口设计，避免将内部信息透露给外部，而在本次作业中，我们设计的接口为几个重要的函数以及类，提供给外部使用。并且在接口设计过程中，也需要与对方团队进行沟通，为之后实现模块互换的工作，打好基础。本次作业设计的接口包括：

  • vector< pair<double, double> > count(vector<string> s)返回一个vector，提供所有交点，方便GUI画图使用
  • int count_int返回int类型字符，即交点个数

Loose Coupling

Loose Coupling是系统设计中的一个强调了组件的独立性的重要概念。引用 维基百科 的话就是说：

松耦合系统中的组件能够被提供相同服务的替代实现所替换。

松耦合系统中的组件不太受相同的平台、语言、操作系统或构建环境的约束。

所以我们的用户在使用接口的时候:

  1. 无需知道内部数据存储逻辑和结构
  2. 仅需使用外层接口的通用数据
  3. 多层次、多粒度的通用接口设计方案

4 计算模块接口的设计与实现过程

松耦合组件设计

由于考虑到有和其他队伍交换dll的可能性,我们和他们详细的讨论了一次组件之间的设计模式.

总结如下:

  • 向量式的直线
  • 利用c++标准类型做数据间的传递通道
  • 组件函数的交叉验证

向量式的直线

我们把一条线\(AB\)描述成\(p(t) = A + t \times \overrightarrow{AB}\)

对于点在线段有\(t \in [0,1]\)，点在射线\(t \in [0,+\infty)\)，点在直线有\(t \in (-\infty,+\infty)\)，很好的解决了点在线上的判断问题。这样的好处是，最大可能的复用上次的代码，便于回归测试。

struct Line {
	int id;
	char tp;
	Point u;
	Point v;
	Line() { id = 0;  tp = 'L'; }
	Line(Point u, Point v) :u(u), v(v) { id = 0; tp = 'L'; }
	Line(Point u, Point v, char tp) :u(u), v(v), tp(tp) { id = 0; }
	bool operator == (const Line& A) const { //判断是否是同一条直线
		if (tp != A.tp) {
			return 0;
		}
		if (tp == 'S') {
			if (u == A.u)
				return v == A.v;
			Point uv = u + v;
			Point auv = A.u + A.v;
			if (uv == A.u)
				return u == auv;
			return false;
		}
		if (tp == 'R') {
			return u == A.u && !dcmp(v.y * A.v.x - A.v.y * v.x);
		}
		return !dcmp(v.y * A.v.x - A.v.y * v.x) && !dcmp((u - A.u) ^ (u - (A.u + A.v)));
	}
	Point point(double t) const {
		return u + v * t;
	}
	bool online(Point x) {
	
	}
	bool online(double len) { // 利用向量形式的特性
		if (tp == 'R') {
			return dcmp(len) >= 0;
		}
		else if (tp == 'S') {
			return dcmp(len) >= 0 && dcmp(1 - len) >=0;
		}
		return 1;
	}
};

其余类（算法类，点类，圆类）

对于点和圆，也是抽象成基本对象来描述。

struct Point {
	double x, y;
	Point(double x = 0, double y = 0) : x(x), y(y) {}
	void read() {
		cin >> x >> y;
	}
	void print() {
		printf("%.10lf %.10lf\n", x, y);
	}
	
	bool operator == (const Point& rhs) const { // for unique
		return (dcmp(x - rhs.x) == 0) && (dcmp(y - rhs.y) == 0);
	}

	bool operator < (const Point& rhs) const { // for sort
		int d = dcmp(x - rhs.x);
		if (d < 0) return true;
		if (d > 0) return false;
		if (dcmp(y - rhs.y)) return true;
		return false;
	}

	friend Point operator + (const Point& lhs, const Point& rhs) {
		return Point(lhs.x + rhs.x, lhs.y + rhs.y);
	}

	friend Point operator - (const Point& lhs, const Point& rhs) {
		return Point(lhs.x - rhs.x, lhs.y - rhs.y);
	}

	friend Point operator / (const Point& lhs, const double& d) {
		return Point(lhs.x / d, lhs.y / d);
	}

	friend Point operator * (const Point& lhs, const double& d) {
		return Point(lhs.x * d, lhs.y * d);
	}

	friend double operator * (const Point& lhs, const Point& rhs) { // dot for vector
		return lhs.x * rhs.x + lhs.y * rhs.y;
	}

	friend double operator ^(const Point& lhs, const Point& rhs) { // cross for vector
		return lhs.x * rhs.y - lhs.y * rhs.x;
	}

	double length() {
		return sqrt(x * x + y * y);
	}

	double length2() {
		return x * x + y * y;
	}
	
	pair<double, double> getPair() { // convert to standard type
		return make_pair(x, y);
	}

};

可以看到点类和pair<double,double>具有很好的相容性和相似性，不过我们定义了一些相关的几何任务函数，不再是没有语义的点对，同样也可以很方便的转换到std::pair<double,double>。

struct Circle {
	Point c;
	double r;
	Circle() {
		c = Point(0, 0);
		r = 0;
	}
	Circle(Point c, double r) :c(c), r(r) {}
	Point point(double a) const {
		return Point(c.x + cos(a) * r, c.y + sin(a) * r);
	}
};

比较有意义的是我们定义了算法类solve，这实际上是一种策略模式的思路把对于同一个需求的策略集中起来。

struct solve {
    
    // 异常相关服务
    int isType(string); // 检查输入是何种类型
    int isSame(string,stsring) // 检查输入是否unique
    
    // 工厂服务
    Line getLine(string); // 根据输入的类型创建适当类型的直线、射线、线段的函数工厂接口
    Circle getCircle(string); // 根据输入的类型创建适当类型的圆的函数工厂接口
    
    // 原子操作
    void getLineInter(Line,Line,vector<Point> &); // 求得线交点，传引用的方式回收答案
    void getCircleInter(Circle,Circle,vector<Point> &); // 求得圆交点，传引用的方式回收答案
    void getLcInter(Linc,Circle,vector<Point> &); // 求得线圆交点，传引用的方式回收答案
    
    // 集合操作
    vector<Point> count_line(vector<Line>); // 求得线集合的交
    vector<Point> count_cir(vector<Circle>); // 求得线集合的交
    
    // 面向UI的接口，由于对面的数据结构未知，需要convert to标准c++支持的类型
    vector< pair<double,double> > count(vector<str>); // 给定需求求得交点集合
    int count_int(vector<str>); // 给定需求求得交点个数
}

通过solve我们把不同层次的需求，封装在了一起，可以很方便的适合多种粒度的询问与测试。粗粒度的GUI测试可以实现，超细粒度的单元测试，和中等粒度的命令行文件测试，都可以应对。

核心封装

注意到solve我们使用的全部是没有副作用的方式的管理和组织任务，而每一次GUI做图，实际上是一次向core提交任务，那么也就是说我们实现了利用消息传递的方式解决繁杂的调用问题。

故可以把上述核心类封装为dll文件和lib文件，方便快速部署在若干个复杂环境下。

同时我们也支持使用.h和.hpp的静态调用方式，便于快速部署命令行应用程序。

5 核心模块内的设计——UML阐释

UML 图显示计算模块部分各个实体之间的关系。

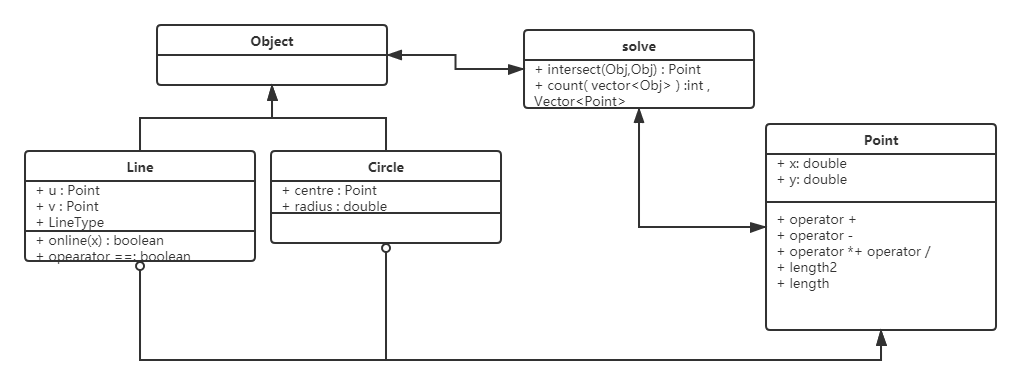
图中详细展示了坐标&点与几何对象两个系统内部的实体关系和两个系统之间的联系
- 在逻辑上Line,Circle都是可相交的几何对象
- 相交的逻辑结构和对象分离设计
- 维护Point所需的相关参数

考虑独立性，我们的部署结构如下

可以便于我们快速的部署

6 性能评估与改进

记录在改进计算模块性能上所花费的时间，描述你改进的思路，并展示一张性能分析图，并展示你程序中消耗最大的函数。

参数的传递优化

求交点的函数如果频繁的返回一个pair会很慢。注意到。

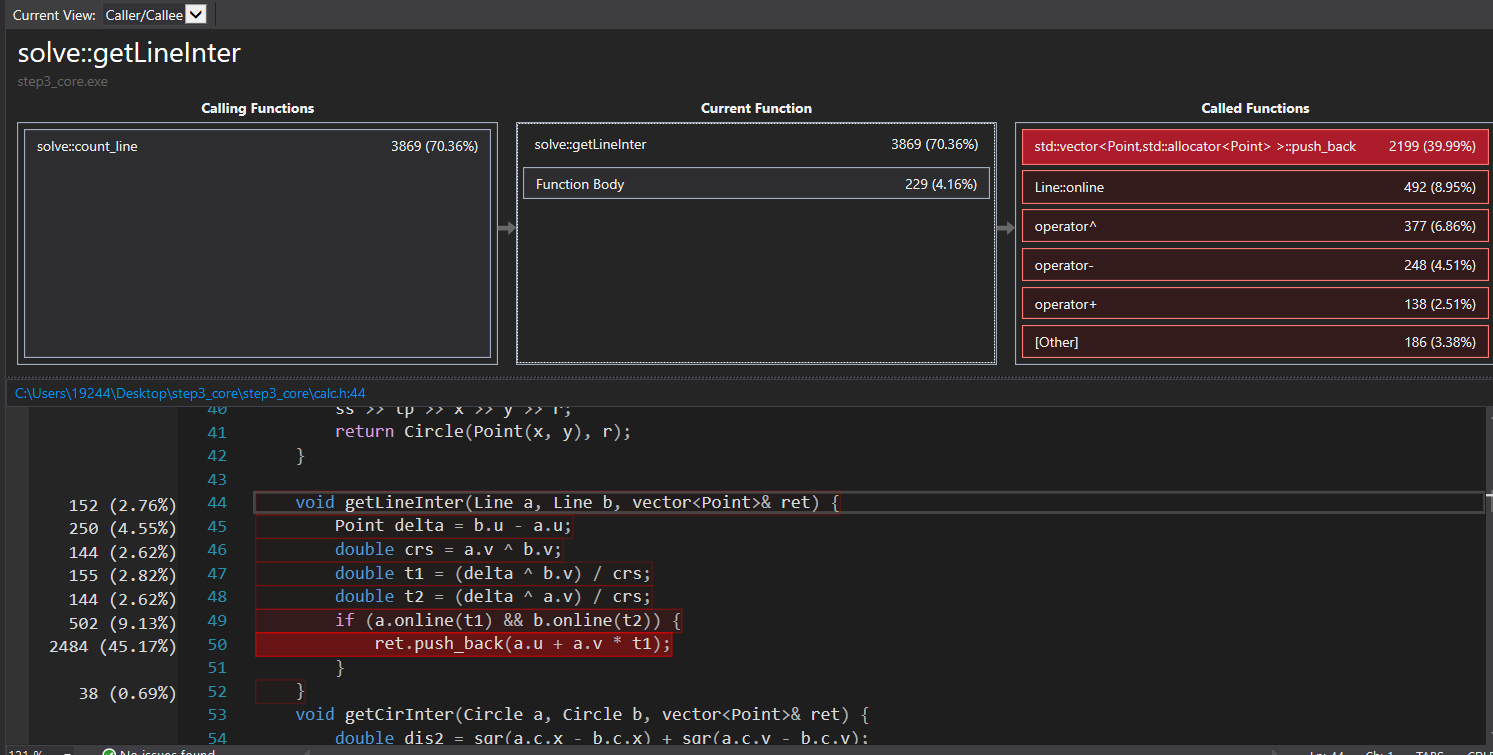
构造器已经占用了大量时间，如果在频繁的做std::move是得不偿失的。

取消hashset或者其他容器的使用


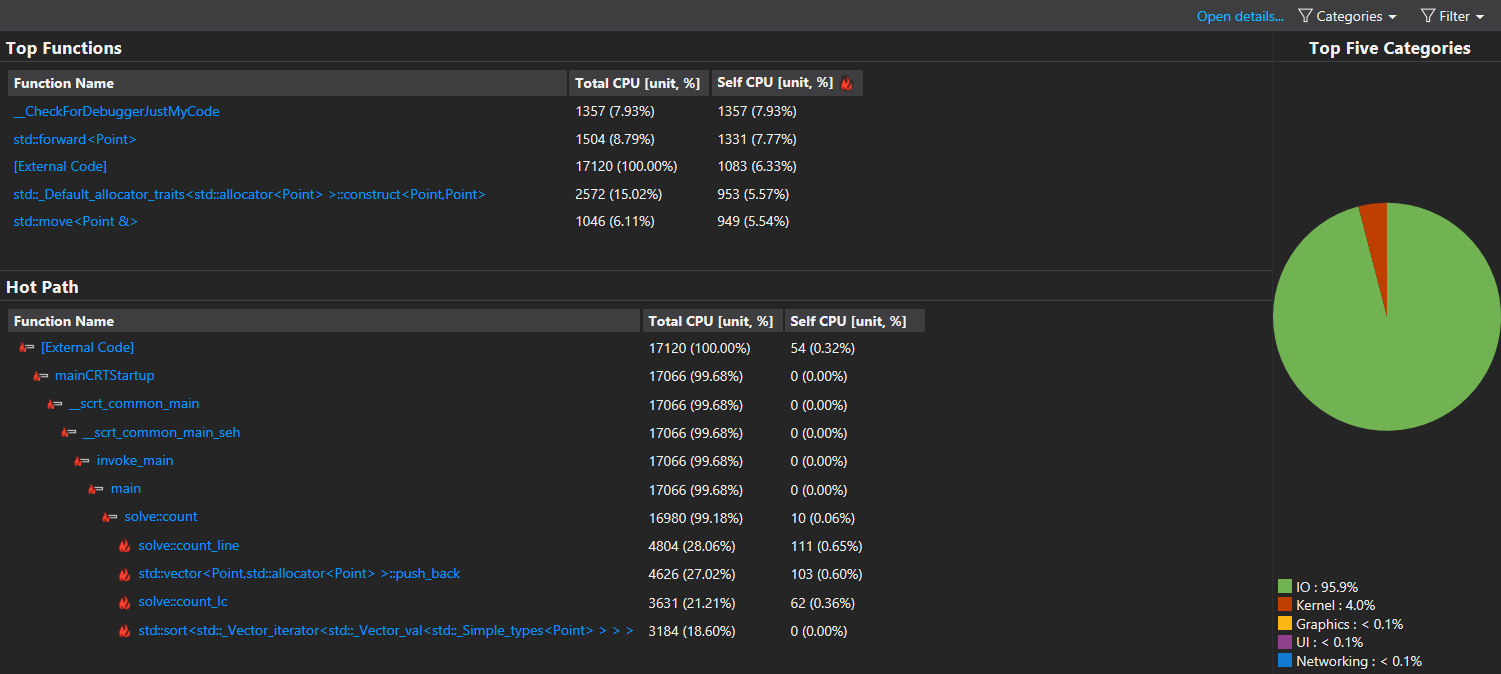
经过这样的优化后，我们最后采用了vector存储所有的交点，最后一次Sort,Unique的方案。效果非常好！

7 Code Contract

契约式设计是一种保障代码质量的手段，其思想是使用某种特殊的语言对接口函数的行为和约束（前置条件、后置条件、不变式等）进行建模和描述，并在编码后对代码进行静态检查（static）、运行时检查(run time)等。

  • 先验条件：为了调用函数，必须为真的条件，在其违反时，函数决不调用，传递好数据是调用者的责任。
  • 后置条件：函数保证能做到的事情，函数完成时的状态，函数有这一事实表示它会结束，不会无休止的循环
  • 不变式：从调用者的角度来看，该条件总是为真，在函数的内部处理过程中，不变项可以为变，但在函数结束后，控制返回调用者时，不变项必须为真。

但是这种设计在我们目前的思路中存在很多缺点:

  1. 程序契约不能代替程序编写，良定义的接口并不意味着会有良定义的实现
  2. 程序契约不能代替单元测试，良定义的接口并非全都可以规范为单元测试
    • 如我们常说的forall, exists等量词，良定义，但是很难做测试
  3. 契约本身的长度超过了代码，而复杂的代码又难以用契约约束

但在设计公有接口时，我们和另一组合作撰写一份自然语言的接口规格文档，用伪代码和数学公式的形式规定前置条件、后置条件和函数行为规范。(最后我们用简明的函数名称，和完成的testfile实现了这一契约的交互)

8 单元测试部分展示

覆盖率展示

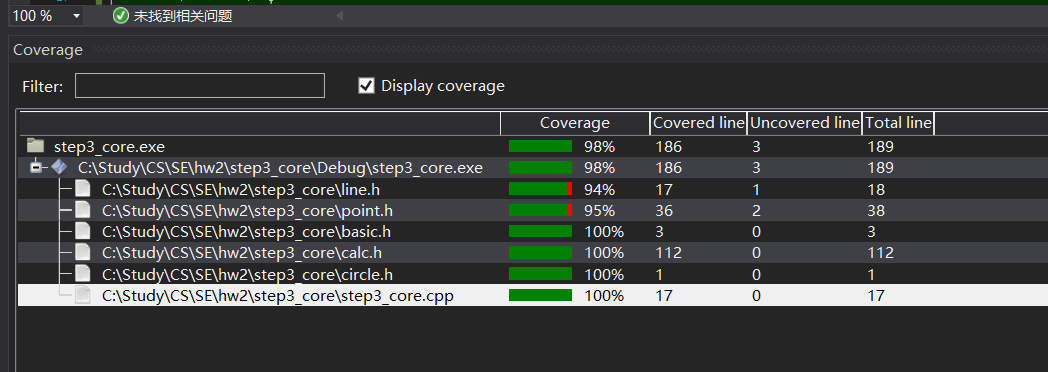
在覆盖率上，我们有极其优秀的效果，可以看到solve的特性使得我们可以展开超细粒度、中等粒度和粗粒度的多样化的测试。

basic.h基础库测试，覆盖率100%，逐行覆盖

calc.h计算任务相关测试，覆盖率100%，逐行覆盖

circle.h圆相关函数测试，覆盖率100%，逐行覆盖

core测试，覆盖率100%，逐行覆盖

point.h和line.h是由于我们有一些接口供其他测试小组测试，所以并未完全覆盖，理论上在其他测试小组的系统下也进行了覆盖测试。

覆盖测试思路

  1. 使用随机强数据

    • 这部分有多个组的同学和我们讨论数据生成
      • 相离线段
      • 相切线段
      • 相交线段
        • 部分重叠线段
        • 完全重叠线段
        • 左对齐线段
        • 右对齐线段
        • 组合测试
      • 相切的圆和线段
      • 相离的圆和线段
        • 相离的圆和线段的延长线有交点

  2. 多种测试的综合测试

    • 随机测试组合
    • edge case组合测试
    • 多次回归测试
    • 其他组的错误数据集测试

  3. 需求测试和异常测试

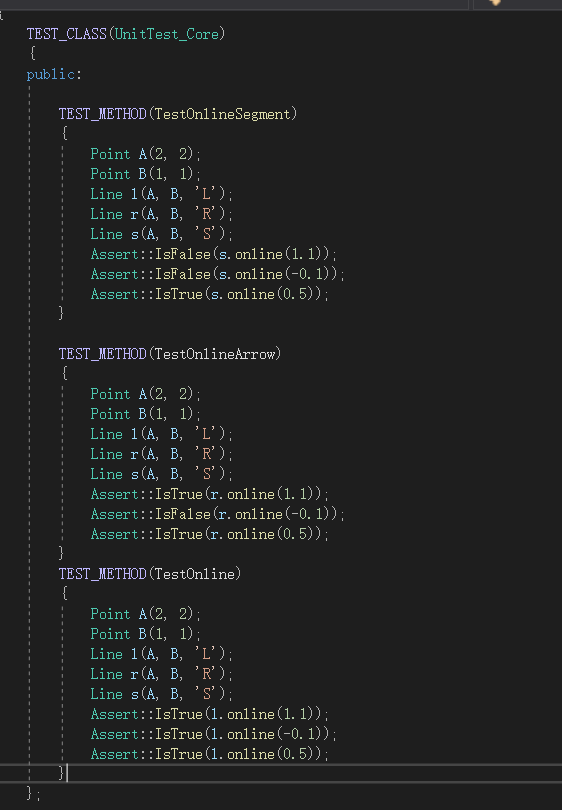
9 异常测试

我们支持异常任务和标准任务同时测试，测试效果如下

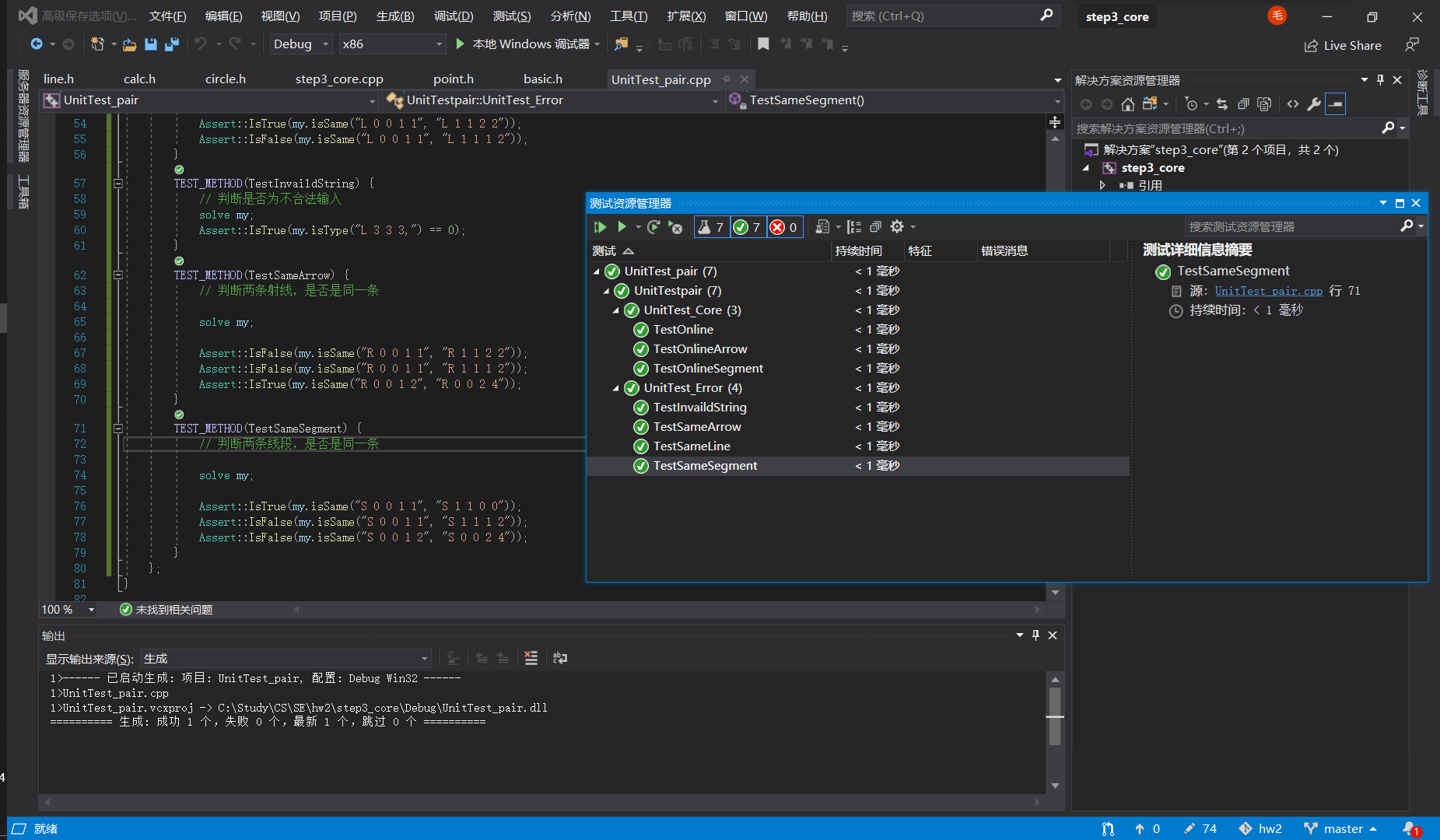
为了使core模块具有高度的兼容性和可扩展性，我们不仅仅是兼容了异常类、try-catch等主流写法，同时我们支持原生的类似windows中的写法：将异常错误码和错误信息打包进struct，在每个函数返回error code。

在上述截图中，我们独立测试了

  1. 不合法的线段
  2. 不合法的直线
  3. 不合法的圆
  4. 不合法的射线
  5. 不合法的奇怪符号
  6. 超过范围的特殊数据
  7. 不合法的调用

可以看到，所有测试均通过。

10 界面模块的详细设计过程

界面模块采用Qt进行开发，如上图所示

  • 左边为输出图像的窗口，采用QCustomPlot模块，可以将一个QWidget提升为画布，提供了一个精美的可以随意移动或是放缩的坐标系，在图中对于所有的交点以及各个线条的端点给出了标注，

    • 直线：QCPItemStraightLine

    • 线段：QCPItemLine

    • 射线：并未提供射线，因此选择使用射线的端点，到其最远点画线段来代替，由于本次所有的参数都存在一个范围，因此可以计算出最远端交点的坐标轴范围，以此来画出线段，代替直线

    • 圆：并未提供画圆的功能，但存在画曲线，因此选择画出圆上均匀的200个点，画出曲线来代替圆

  • 右侧为控制台，供用户进行数据的添加、删除、加载文件以及获取输出

    • btn_run：当用户完成数据的编辑后，点击run按钮，即可在左边绘制图像，同时在下方的文本框中读取到数据。
    • btn_import：为用户提供导入文件的接口，用户点击import后，会弹出文件选择窗口，选择恰当的文本文件，即可将文本文件内的内容读取到下方的显示框中，进行进一步的操作
    • Line：为了防止用户的随意输入，增加程序的运行压力，此处选择下拉框将用户的选择局限在正确的类型中，并采用数字输入框，保证用户输入数字的范围，尽量避免不必要的麻烦，需要用户输入两个端点的横纵坐标
    • Circle：同上，但圆并没有过多的选项，同时需要用户输入圆的圆心，以及圆的半径
    • descript_list：显示用户对于输入图像的描述，格式为Type Data1 Data2 Data3
    • btn_delete：可以对descript_list中的对象进行删除
    • btn_clear：可以清楚descript_list中的所有对象
    • btn_add：根据所在部份调整好参数后，将描述添加到descript_list

  • Num of Nodes：输出交点个数

11 界面模块与计算模块的对接

core模块为UI提供了两个外部接口

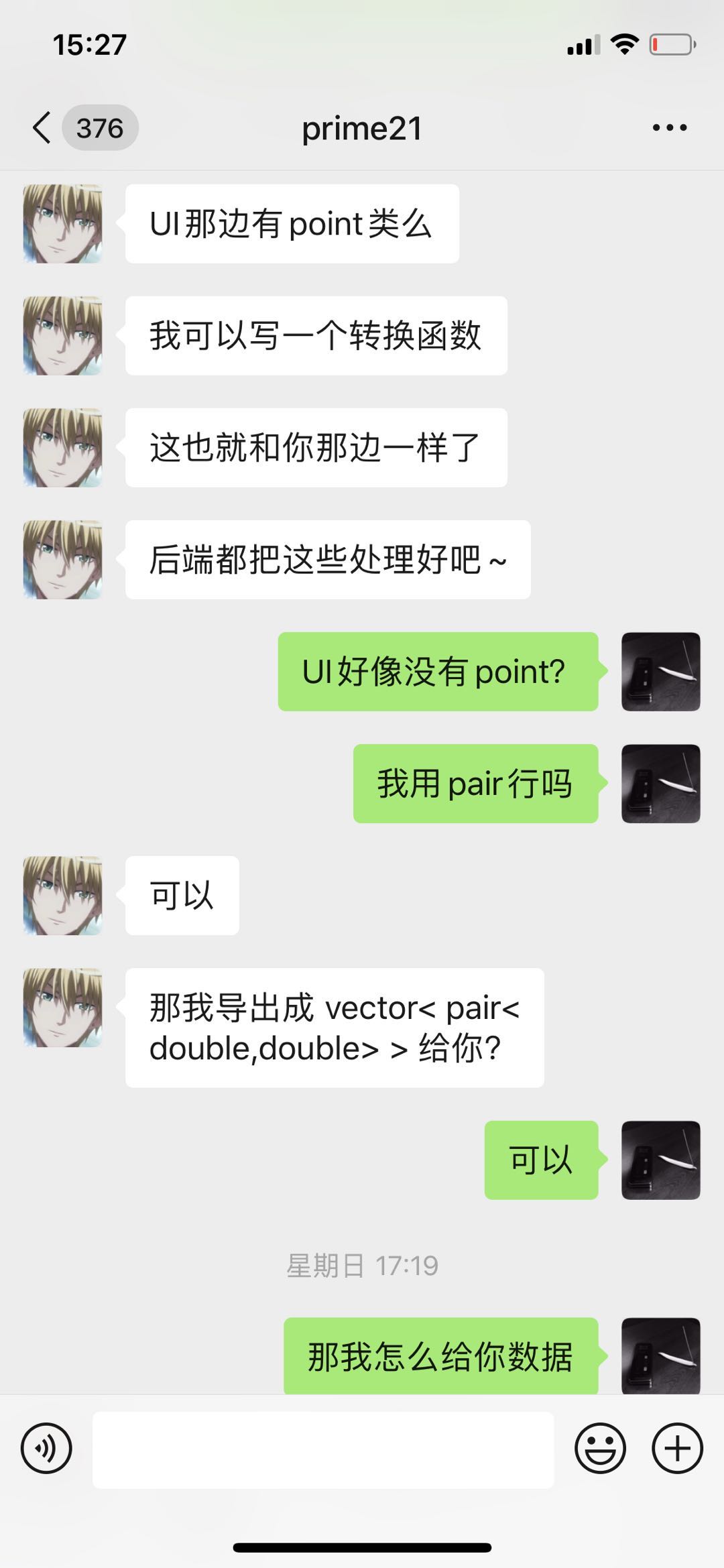
  • vector< pair<double, double> > count(vector<string> s)
    • 将所有的数据数据整合成一个vector<string>的形式，传输给计算模块，存储格式为type data1 data2 data3，返回值设定为vector<pair<double, double>>格式，即包含了所有需要在图上标注处的点的坐标
  • int count_int
    • 将所有的数据数据整合成一个vector<string>的形式，传输给计算模块，存储格式为type data1 data2 data3，返回值设定为int格式，即问题要求的所有交点的个数

12描述结对的过程

  • 在项目一开始，两人都先暴力实现了新增要求的功能，并进行对拍测试，我的的正确率较高，因此进行分工，我负责后端core模块的编写，qxh负责前端UI模块的编写
  • 使用微信、QQ进行项目的交流，同时有使用Tim的屏幕共享功能进行连线，讨论了扫描线算法的原理，以及具体实现，但在后续的具体实现中，发现扫描线算法的代码中漏洞过多，于是选择保证程序正确性为前提，放弃了扫描线算法，选择使用暴力计算，并在暴力的基础上对程序优化
  • 以下为交流过程中的截图


13 十三. 看教科书和其它参考书，网站中关于结对编程的章节，说明结对编程的优点和缺点。同时描述结对的每一个人的优点和缺点在哪里（要列出至少三个优点和一个缺点）

  • 优点：
    • 两个人共同完成项目，好的分工给可以减轻双方工作量，大大提高工作的完成的速度
    • 两人可以相互监督，相互提醒，避免出现ddl选手的情况
    • 可以相互检查代码，自己写的bug往往自己难以看出，而互相检查代码就比较容易找到隐藏的bug
  • 缺点：
    • 两人代码风格存在差异，需要时间去磨合
    • 两人作息时间存在差异，且由于疫情原因，无法十分便捷的找到对方，可能出现一段时间找不到对方的情况，需要实现约好
    • 两人编写代码，需要给对方讲解代码的使用，需要耗费一定的时间

我与队友的缺点：

队友 我
优点 push我，认真，负责，UI开发技术强，人好，善良，好学，积极合作，善于分享知识 算法基础扎实，且编程能力强，代码速度快
缺点 算法能力比较不足，之前没有接触过扫描线算法 缺少一些耐心

15 支持松耦合

我们选择xsy团队完成附加题松耦合的工作

我们两组事先进行了大概的交流，UI的设计类似，并且警经过后期的修改，完成了双方接口的支持，几乎共用一套接口，除了对方UI还支持直接在图像中完成线段的删除，因此我们多增加了deletecCirle()以及deleteLine()的接口，并在互换头文件以及动态链接库后，实现了双方UI的正常工作。

此处展示未使用对方dll文件以及.h文件后的运行结果，与之前的运行结果完全一致

同样对方也可以使用我们的dll

posted @ 2020-03-24 18:18  I_love_SE_forever  阅读(504)  评论(3)  编辑  收藏  举报