第一次软件工程个人项目作业——algo for intersection

个人项目作业-求图形交点个数

• 教学班级：005
• 项目地址：https://github.com/prime21/IntersectProject.git

项目	内容
本作业属于北航 2020 年春软件工程	博客园班级连接
本作业是本课程个人项目作业	作业要求
我在这个课程的目标是	收获团队项目开发经验，提高自己的软件开发水平
这个作业在哪个具体方面帮助我实现目标	体验MSCV开发的pipeline

解题思路

根据需求描述，我们不难得到所需软件的运行流程，总体而言分为三步：

• 解析命令行参数，获取输入文件与输出文件的路径
• 从输入文件中获取输入，并对图形参数进行解析，存储于相应的数据结构中
• 求解图形之间的交点个数，并输出

1. 两条直线的交点公式，联立

\[A_1 x + B_1 y + C_1 = 0 \\ A_2 x + B_2 y + C_2 = 0 \]

解得

\[X = \frac{B_1 C_2 - B_2 C_1} {A_1 B_2 - A_2 B_1} \\ Y = \frac{B_1 C_2 - B_2 C_1} {A_1 B_2 - A_2 B_1} \]

2. 两个圆的交点公式\(C_1(O_1,r_1),C_2(O_2,r_2)\)

   不相交的情况$$ |O_1O_2| < |r_1-r_2|$$ 或者 \(|O_1O_2| > r_1+r_2\)

   其余情况，考察连心线和交点弦的垂直关系，先求交点弦和连心线的交点\(P\)

   \(P = O_1 + \overrightarrow {i_{O_1O_2}} \times a\)

   其中$a = \frac {r_1^2 - r_2^2 + d^2} {2d} $

   然后在垂直方向上得到交点\(P' = P \pm \overrightarrow j \times h\)

   \(\overrightarrow j\)是\(\overrightarrow i\)的法向量，\(h = \sqrt{r_1^2 - a^2}\)

3. 直线和圆的交点公式，考虑直线为向量式\(u = u_0 + t (u_1-u_0)\)，圆为\(C(O,r)\)

   由\(|uO| = r\)消去得\(|u_0 + t (u_1-u_0) - O| = r\) 为关于\(t\)的一个二次方程，解得两个\(t\)，得交点

设计

数据结构

基本的向量运算类型

struct inter {
	double x;
	double y;
	inter() { x = 0; y = 0; }
	inter(double x, double y) : x(x), y(y) {}
	inter(poi p) : x(p.first * 1.), y(p.second * 1.) {}
	bool operator == (const inter& rhs) const {
		return dcmp(x - rhs.x) == 0 && dcmp(y - rhs.y) == 0;
	}
	bool operator < (const inter& rhs) const {
		int d = dcmp(x - rhs.x);
		if (d < 0) return true;
		if (d > 0) return false;
		if (dcmp(y - rhs.y) < 0) return true;
		return false;
	}

	friend inter operator + (const inter& lhs, const inter& rhs) {
		return inter(lhs.x + rhs.x, lhs.y + rhs.y);
	}

	friend inter operator - (const inter& lhs, const inter& rhs) {
		return inter(lhs.x - rhs.x, lhs.y - rhs.y);
	}

	friend inter operator / (const inter& lhs, const double& d) {
		return inter(lhs.x / d, lhs.y / d);
	}
	
	friend inter operator * (const inter& lhs, const double& d) {
		return inter(lhs.x * d, lhs.y * d);
	}

	friend double operator * (const inter& lhs, const inter& rhs) {
		return lhs.x * rhs.x + lhs.y * rhs.y;
	}

	double length() {
		return sqrt(x * x + y * y);
	}

	double length2() {
		return x * x + y * y;
	}
};

复杂度分析

考虑到枚举所有线和圆的交点情况，并对所有交点排序，复杂度是\(O( n ^2 + m \log m)\)其中\(n\)是线和圆的个数，\(m\)是交点个数。

代码实现

代码组织

三种交点的函数

void addLineInter(int i, int j) {
	line *lhs = (line *)(pro[i]);
	line *rhs = (line *)(pro[j]);
	
	long long D = (lhs->A * rhs->B) - (rhs->A * lhs->B);

	if (D == 0) return ;
	double xx = (lhs->B * 1. * rhs->C) - (rhs->B * lhs->C);
	double yy = (lhs->A * 1. * rhs->C) - (rhs->A * lhs->C);

	gb_in.push_back(inter(xx / D, yy / D));
}

void addCircleInter(int i, int j) {
	circle* lhs = (circle*)(pro[i]);
	circle* rhs = (circle*)(pro[j]);

	long long dis = (lhs->o.first - rhs->o.first) * (lhs->o.first - rhs->o.first) + (lhs->o.second - rhs->o.second) * (lhs->o.second - rhs->o.second);

	if (dis > (lhs->r + rhs->r) * (lhs->r + rhs->r)) return; 
	if (dis < (lhs->r - rhs->r) * (lhs->r - rhs->r)) return;
	
	double alpha = dis + lhs->r * lhs->r - rhs->r * rhs->r;
	alpha /= 2 * sqrt(dis);

	double h = std::sqrt(lhs->r * lhs->r - alpha * alpha);

	inter o1o2 = inter(rhs->o) - inter(lhs->o);
	o1o2 = o1o2 / o1o2.length();
	inter vert = inter(o1o2.y, -o1o2.x);
	inter P = inter(lhs->o) + o1o2 * alpha;
	inter Q = P + vert * h;
	gb_in.push_back(Q);
	Q = P - vert * h;
	gb_in.push_back(Q);
}

void addLcInter(int i, int j) {
	line* lhs = (line*)(pro[i]);
	circle* rhs = (circle*)(pro[j]);

	inter li = inter(lhs->b) - inter(lhs->a);
	inter lc = inter(lhs->a) - inter(rhs->o);

	double A = li.length2();
	double B = (lc * li) * 2;
	double C = lc.length2() - (rhs->r) * (rhs->r);

	double delta = B * B - 4 * A * C;
	if (delta >= 0) {

		delta = sqrt(delta);

		double x1 = (delta - B) / (2 * A);
		double x2 = (-delta - B) / (2 * A);

		inter t1 = inter(lhs->a) + li * x1;
		inter t2 = inter(lhs->a) + li * x2;
		gb_in.push_back(t1);
		gb_in.push_back(t2);
	}
}

不同情况下的返回值处理

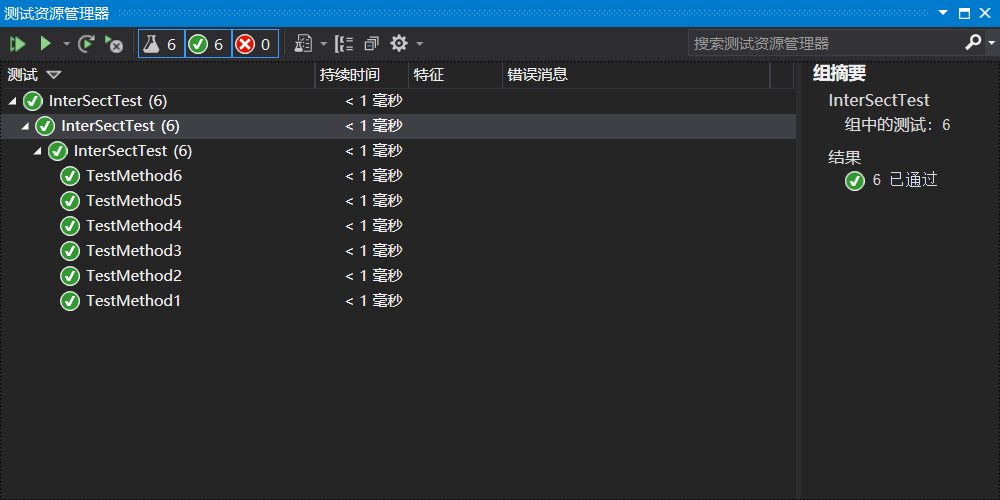
测试

使用了OpenCPPCoverage

代码质量分析

Reshaper C++

性能改进

1. 扫描线做法，可以观察交点前后的关系如下：

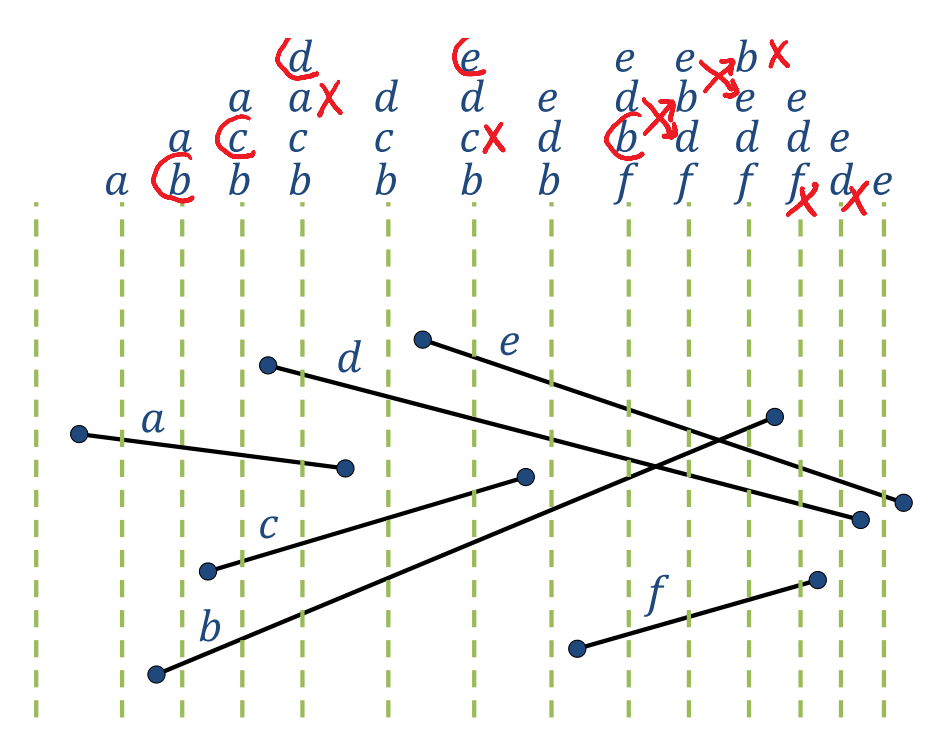
注意到直线相交之后两条直线在y轴方向的大小关系发生了一次改变

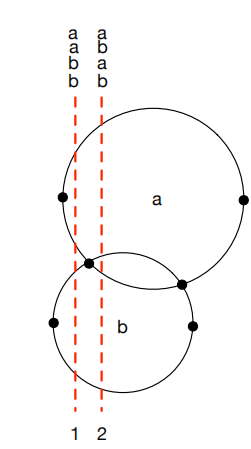
同理，圆在相交的时候，某个圆的上半圆和某个圆的下半圆的位置关系也发生了一次改变

故可以维护一个关于x轴的扫描线，线上的每一个点需要标记为L(x, k) 或者 C(O,r,up/down) 随时计算y轴对应的值。

在每次插入新点的时候，需要考察最靠近的两个点是否会与其相交，如果会需要插入事件。

故需要维护一个序列支持查询前驱后继，删除和添加元素，采用平衡树可以完成这一任务。

故这样的时间复杂度是\(O(n \log n + k)\)的。性能得到了提升

做法需要解决一些问题：

• 多线共点，这样可能会产生多个同时间的时间点，和交叉关系
• 圆的上下半圆自交问题
• 圆的变换关系

事后总结

由于本次任务的需求是确定的，没有太多需要揣测的地方，因此需求分析花费的时间比较少。

PSP 表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
· Estimate	· 估计这个任务需要多少时间	5	5
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	15	15
· Design Spec	· 生成设计文档	10	10
· Design Review	· 设计复审 (和同事审核设计文档)	0	0
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	0	0
· Design	· 具体设计	60	90
· Coding	· 具体编码	240	240
· Code Review	· 代码复审	10	10
· Test	· 测试（自我测试，修改代码，提交修改）	60	60
Reporting	报告
· Test Report	· 测试报告	10	10
· Size Measurement	· 计算工作量	10	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	30
	合计	450	480