牛客多校第九场 J Jam

题意：有一个十字路口，每个方向都有三种转向，一共12种，如图：

 

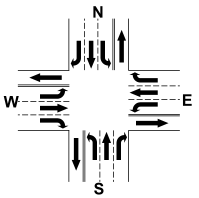
每秒放行一部分方向上的车，每个转向1秒最多开出来一辆，问不冲突的情况下最短多久能把车放完。

思路：

赛场上感觉是网络流但是已经是没时间写了，然后赛后发现这道题的图也不大会建。

这时候看到某个B站关注的大佬的题解，写的非常巧妙

原视频链接：https://www.bilibili.com/video/BV1344y1y71d

 建议看原视频，这里我简单总结一下，方便自己复习

首先右转肯定是不用考虑的，因为都贴着弯，最后取个最值就行。

然后看左转和直行，可以发现只有4种情况

1.面对面的都直行

2.面对面的都左转

3.同个方位又直行又左转

4.直行并且左手边左转

我们把直行和左转的待行车辆列个表

 

 

 

可以发现对于前面三种情况，就是对于(a1,a3,b1,b3),(a2,a4,b2,b4)这两个4宫格单独操作。

然后对于这样一个模型的最小步数是有结论的

答案就是max(a+d,b+c)

我们学校的一个学长在视频下面做了简短的证明

 

 然后对于最后一种情况，我们n^3*4枚举削减的情况然后再计算就行了。

下附代码：

#include<bits/stdc++.h>
using namespace std;
const int INF=0X3f3f3f3f;
int a[105],b[105],c[105];
int cal(int a,int b,int c,int d){
    return max(max(b,0)+max(c,0),max(a,0)+max(d,0));
}
int main(){
    int T;
    scanf("%d",&T);
    while (T--){
        for(int i=1; i<=4; i++){
            for (int j=1; j<=4; j++){
                int x;
                scanf("%d",&x);
                if (i==j+1 || (i==1 && j==4)){
                    c[i]=x;
                }
                else if (abs(i-j)==2){
                    a[i]=x;
                }
                else if (i!=j){
                    b[i]=x;
                }
            }
        }
        int res=INF;
        for (int i=0; i<=100; i++){
            for (int j=0; j<=100; j++){
                for (int k=0; k<=100; k++){
                    res=min(res,i+j+k+cal(a[1]-i,b[1],a[3]-k,b[3]-j)+cal(a[2]-j,b[2]-i,a[4],b[4]-k));
                    res=min(res,i+j+k+cal(a[1]-i,b[1]-k,a[3],b[3]-j)+cal(a[2]-j,b[2]-i,a[4]-k,b[4]));
                    res=min(res,i+j+k+cal(a[1]-i,b[1]-k,a[3]-j,b[3])+cal(a[2],b[2]-i,a[4]-k,b[4]-j));
                    res=min(res,i+j+k+cal(a[1],b[1]-k,a[3]-j,b[3]-i)+cal(a[2]-i,b[2],a[4]-k,b[4]-j));
                } 
            }
        }
        for (int i=1; i<=4; i++){
            res=max(res,c[i]);
        }
        printf("%d\n",res);
    }
}

之后有时间看一下这题怎么建图，补一下网络流做法