2021牛客多校 第七场 F xay loves trees (线段树+括号化序列
题意:给定两个树,求一个最大的点集,使得第一棵树上成一条链并且第二课树上不互为祖先
思路:赛场上不知道括号化序列这个知识点,所以想不到什么好办法能快速处理互为祖先这件事。赛后B站看了题解学会的
括号化序列:根据一棵树的dfs序,将其入栈与出栈的时间戳记录下来, 可以发现,每一棵子树的出入时间必定被根节点包含,如图;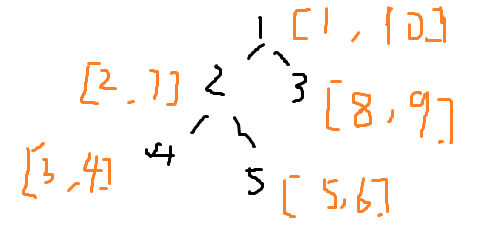
所以一棵树的祖先关系就可以转换成数轴上的一段段区间关系
那么处理这种区间关系最好的就是线段树了。
我们先根据第二棵树,dfs找出括号化序列,然后再遍历第一棵树。
遍历的时候维护一棵线段树,用于维护当前区间上深度最大的结点。
因为我们要的是连续的链,所以如果树上每一个结点的贡献就是其向上找最近的冲突点。
代码有几个注意点:1.因为某段区间上的点可能会被pop完,所以要开一个vector来保存区间上的点,方便回溯与找最后一个点,另外开一个mx数组,记录当前区间上的最大值
查询的时候对于过程中找到的区间,ret取的max值应该是vector里面的而不是mx里面的,因为mx会取到不属于查询区间的值。
遍历第一棵树的时候注意要记录下来当前冲突的最晚节点。因为产生冲突的不一定是当前节点。
下附代码:

1 #include<bits/stdc++.h> 2 #define p2 (p<<1) 3 #define p3 (p<<1|1) 4 using namespace std; 5 const int maxn=3e5+5; 6 vector<int> G1[maxn]; 7 vector<int> G2[maxn]; 8 int stackd,dfnl[maxn],dfnr[maxn]; 9 vector<int> tr[maxn<<3]; 10 int mx[maxn<<3]; 11 int res=0,n; 12 int d[maxn]; 13 void dfs1(int x,int pre){ 14 dfnl[x]=++stackd; 15 for (auto y:G2[x]){ 16 if (y!=pre){ 17 dfs1(y,x); 18 } 19 } 20 dfnr[x]=++stackd; 21 } 22 void build(int l,int r,int p){ 23 if (l==r){ 24 mx[p]=0; 25 tr[p].clear(); 26 return ; 27 } 28 int mid=(l+r)>>1; 29 build(l,mid,p2); 30 build(mid+1,r,p3); 31 } 32 void pushup(int l,int r,int p){ 33 mx[p]=0; 34 if (tr[p].size()) mx[p]=*(tr[p].end()-1); 35 if (l<r){ 36 mx[p]=max(mx[p],mx[p2]); 37 mx[p]=max(mx[p],mx[p3]); 38 } 39 } 40 void update(int l,int r,int le,int ri,int p,int val){ 41 if (l==le && r==ri){ 42 if (val>0) tr[p].push_back(d[val]); 43 else tr[p].pop_back(); 44 pushup(l,r,p); 45 return ; 46 } 47 int mid=(l+r)>>1; 48 if (ri<=mid) update(l,mid,le,ri,p2,val); 49 else if (le>mid) update(mid+1,r,le,ri,p3,val); 50 else update(l,mid,le,mid,p2,val),update(mid+1,r,mid+1,ri,p3,val); 51 pushup(l,r,p); 52 } 53 int query(int l,int r,int le,int ri,int p){ 54 if (l==le && r==ri){ 55 return mx[p]; 56 } 57 int mid=(l+r)>>1,ret=0; 58 if (tr[p].size()) ret=*(tr[p].end()-1); 59 if (ri<=mid) ret=max(ret,query(l,mid,le,ri,p2)); 60 else if (le>mid) ret=max(ret,query(mid+1,r,le,ri,p3)); 61 else ret=max(max(query(l,mid,le,mid,p2),query(mid+1,r,mid+1,ri,p3)),ret); 62 return ret; 63 } 64 void dfs2(int x,int dis,int pre){ 65 dis=max(dis,query(1,2*n,dfnl[x],dfnr[x],1)); 66 res=max(res,d[x]-dis); 67 update(1,2*n,dfnl[x],dfnr[x],1,x); 68 for (auto y:G1[x]){ 69 if (y!=pre){ 70 d[y]=d[x]+1; 71 dfs2(y,dis,x); 72 } 73 } 74 update(1,2*n,dfnl[x],dfnr[x],1,-x); 75 } 76 int main(){ 77 int T; 78 scanf("%d",&T); 79 while (T--){ 80 scanf("%d",&n); 81 stackd=0; 82 res=1; 83 for (int i=1; i<=n; i++){ 84 d[i]=0; 85 G1[i].clear(); 86 G2[i].clear(); 87 } 88 d[1]=1; 89 for (int i=1; i<n; i++){ 90 int x,y; 91 scanf("%d%d",&x,&y); 92 G1[x].push_back(y); 93 G1[y].push_back(x); 94 } 95 for (int i=1; i<n; i++){ 96 int x,y; 97 scanf("%d%d",&x,&y); 98 G2[x].push_back(y); 99 G2[y].push_back(x); 100 } 101 dfs1(1,0); 102 build(1,2*n,1); 103 dfs2(1,0,0); 104 printf("%d\n",res); 105 } 106 }


