【题解】鲳数

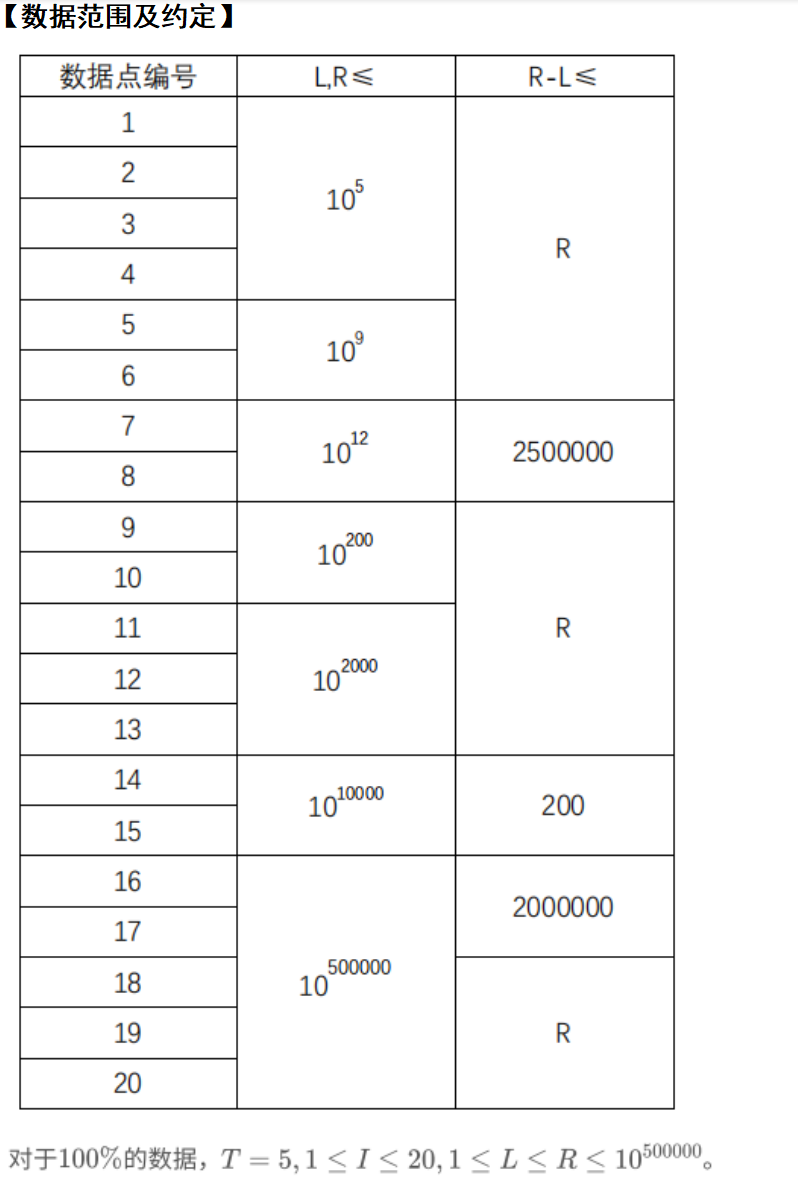
题面

 

 

数位DP

考虑先记从1~9999...999(i个9)中鲳对的数量为$f_i$。

记从1~9999...999(i个9)中数位j的数量为$ff_{ij}$，然后发现所有$ff_ix$都是相等的，就只记一个。

（下面代码 pw10[i] 为 $10^i$）

for(int i=1;i<=500000;i++){
    f[i]=f[i-1]*10%998244353;
    ff[i]=(ff[i-1]*10+pw10[i-1])%998244353;
    for(int j=0;j<10;j++)
        for(int k=0;k<j;k++){
            f[i]+=ff[i-1];
            f[i]%=998244353;
        }
//    cerr<<i<<" "<<f[i]<<endl;
}

 

容易想到差分，记 $f(l,r)$ 为区间 $[l,r]$ 的鲳对数量，那么：$f(l,r)=f(1,r)-f(1,l-1)$，由于我们不好求 $l-1$，所以可以将 $f(1,l-1)$ 转化为 $f(1,l)-l的鲳对个数$。

 

while(t--){
    cin>>l>>r;
    printf("%lld\n",(get(r)-get(l)+getone(l)+998244353)%998244353);
}

 

get函数即为求$f(1,x)$的鲳对个数。

我们可以从高往低求每一位的答案。首先对于每一位$i$（假设那位上的数字是 $a_i$），可以求出$i$位后面独立的鲳对个数，即$f_{i-1}$。但由于你可以是0xxx，1xxx，2xxx……从$0\sim a_i-1$共 $a_i$ 个数，所以要乘 $a_i$，之所以不取 $a_i$ 是因为它不是完整的 1~9999...999。

接着求当前位对于后续位的贡献，因为当前位只是 $\le a_i$，所以要分 $< a_i$ 和 $= a_i$ 两种来处理。如果是 $< a_i$，那么直接枚举 $j$ 从 $0\sim a_i-1$，所有小于 $j$ 的数($j$ 个)都可以提供 $ff_{i-1}$ 的贡献。当等于 $a_i$ 的时候，因为我们一直不知道剩余位数里有多少个指定数字，所以先记到一个标记数组里，每一次当下一个 $< a_j$ 的位数出现的时候加上 < 它数字的数量个 $ff_{j-1}$就行了，$< a_j$的非负整数共 $a_j$ 个（因为有0），所以还要乘以 $a_j$。

处理完后续位的贡献，接着还要处理当前位与前面位的贡献。

如果当前位 $< a_i$，那么前面 > 这个数的就会产生个数 $\times$ 后面数字数量（即 $10^{i-1}$）个贡献。

如果当前位 $= a_i$，那么前面 > 这个数的就会产生个数 $\times$ 后面数字数量（即后面数字所组成的数）个贡献。

最后把当前位加入为前面的标记数组里就行了

代码因为string第一位是最高位，所以求的时候是从0枚举到$s.size()-1$的，马蜂有点奇怪，常数还大，建议不看。

真的要看吗？

#include<bits/stdc++.h>
using namespace std;
namespace estidi{
	long long now[13],f[500003],ff[500003],last[500003],pw10[500003];
	long long getone(string s){
		int ans=0;
		for(int i=0;i<s.size();i++){
			now[s[i]-'0']++;
			for(int j=s[i]-'0'+1;j<10;j++){
				ans+=now[j];
				ans%=998244353;
			}
		}
		for(int i=0;i<10;i++)
			now[i]=0;
		return ans;
	}
	long long get(string s){
		long long ans=0;
		last[s.size()]=0;
		for(int i=s.size()-1;i>=0;i--)//预处理后面数字所组成的数
			last[i]=(last[i+1]+pw10[s.size()-i-1]*(s[i]-'0'))%998244353;
		for(int i=0;i<s.size();i++){
			ans+=f[s.size()-i-1]*(s[i]-'0');
			ans%=998244353;
			for(int j=0;j<s[i]-'0';j++){
				ans+=ff[s.size()-i-1]*j%998244353;
				ans%=998244353;
			}
			for(int j=0;j<10;j++){
				ans+=ff[s.size()-i-1]*now[j]%998244353*(s[i]-'0')%998244353*j%998244353;
				ans%=998244353;
			}
			for(int j=0;j<s[i]-'0';j++)
				for(int k=j+1;k<10;k++)
					ans+=now[k]*pw10[s.size()-i-1];
			for(int k=s[i]-'0'+1;k<10;k++)
				ans+=now[k]*(last[i+1]+1);
			now[s[i]-'0']++;
		}
//		cout<<s<<":"<<ans<<endl;
		for(int i=0;i<10;i++)
			now[i]=0;
		return ans;
	}
	int main(){
//		freopen("pair.in","r",stdin);
//		freopen("pair.out","w",stdout);
		pw10[0]=1;
		for(int i=1;i<=500000;i++)
			pw10[i]=pw10[i-1]*10%998244353;
		int t,tc;
		string l,r;
		scanf("%d%d",&t,&tc);
		for(int i=1;i<=500000;i++){
			f[i]=f[i-1]*10%998244353;
			ff[i]=(ff[i-1]*10+pw10[i-1])%998244353;
			for(int j=0;j<10;j++)
				for(int k=0;k<j;k++){
					f[i]+=ff[i-1];
					f[i]%=998244353;
				}
//			cerr<<i<<" "<<f[i]<<endl;
		}
		while(t--){
			cin>>l>>r;
			printf("%lld\n",(get(r)-get(l)+getone(l)+998244353)%998244353);
		}
		return 0;
	}
}
int main(){
	estidi::main();
	return 0;
}