排序--归并排序

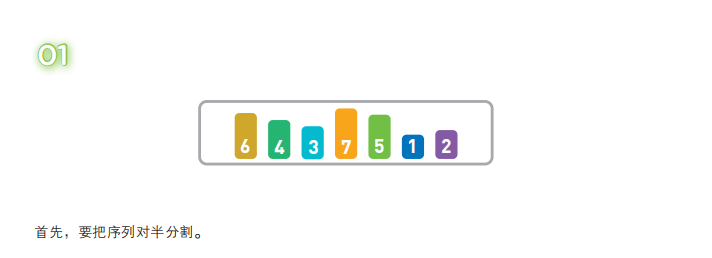
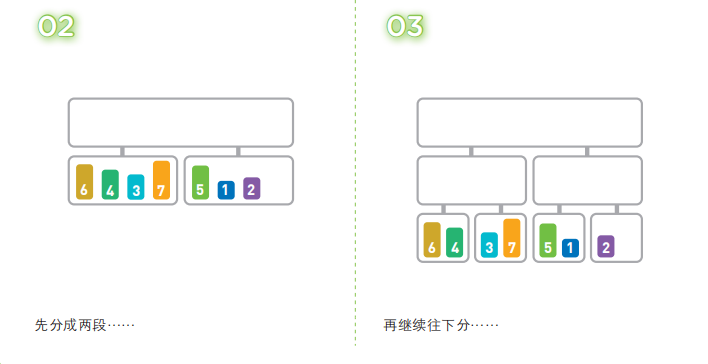
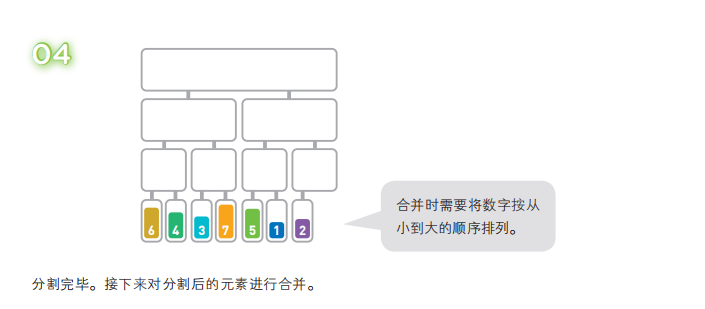
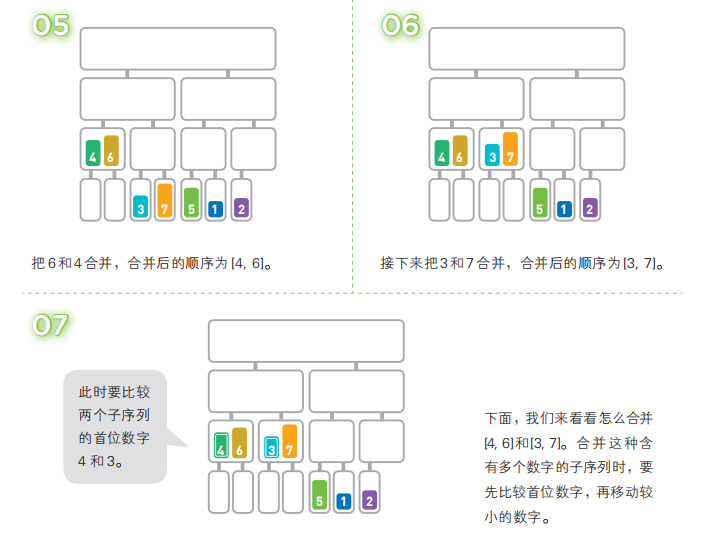
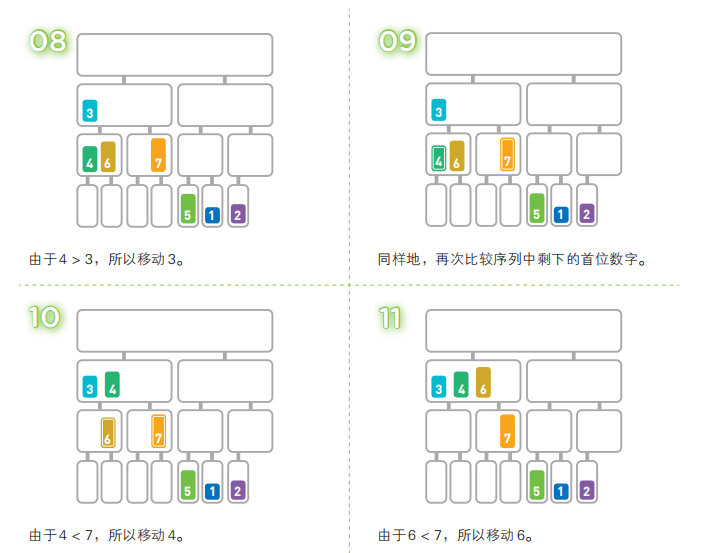
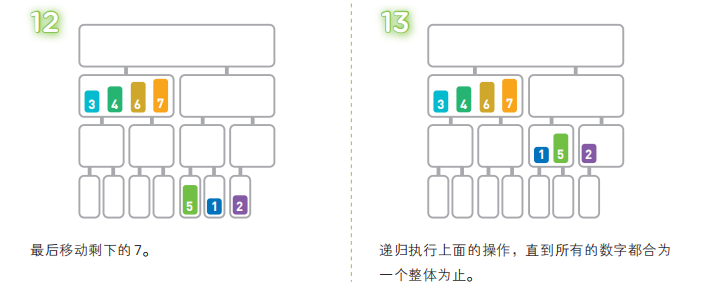
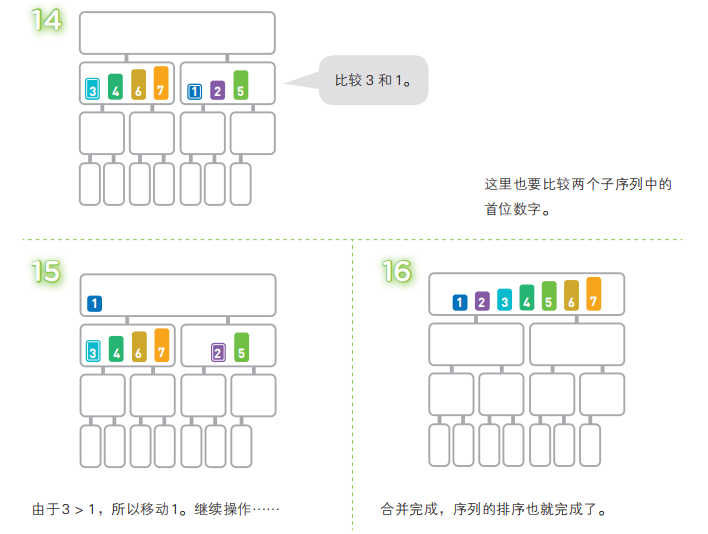
　　归并排序算法会把序列分成长度相同的两个子序列，当无法继续往下分时（也就是每个子序列中只有一个数据时），就对子序列进行归并。归并指的是把两个排好序的子序列合并成一个有序序列。该操作会一直重复执行，直到所有子序列都归并为一个整体为止。

 

 

 

 

 

 

 

 

 

 

 

 

 

 解说

　　归并排序中，分割序列所花费的时间不算在运行时间内（可以当作序列本来就是分割好的）。在合并两个已排好序的子序列时，只需重复比较首位数据的大小，然后移动较小的数据，因此只需花费和两个子序列的长度相应的运行时间。也就是说，完成一行归并所需的运行时间取决于这一行的数据量。看一下上面的图便能得知，无论哪一行都是 n 个数据，所以每行的运行时间都为 O(n)。而将长度为 n 的序列对半分割直到只有一个数据为止时，可以分成 log2n 行，因此，总共有 log2n 行。也就是说，总的运行时间为 O(nlogn)，这与前面讲到的堆排序相同

public static void main(String[] args) {

        int arr[] = {7, 5, 3, 2, 4, 1，6};

        //归并排序
        int start = 0;
        int end = arr.length - 1;
        mergeSort(arr, start, end);
    }

    public static void mergeSort(int[] arr, int start, int end) {
        //判断拆分的不为最小单位
        if (end - start > 0) {
            //再一次拆分，知道拆成一个一个的数据
            mergeSort(arr, start, (start + end) / 2);
            mergeSort(arr, (start + end) / 2 + 1, end);
            //记录开始/结束位置
            int left = start;
            int right = (start + end) / 2 + 1;
            //记录每个小单位的排序结果
            int index = 0;
            int[] result = new int[end - start + 1];
            //如果查分后的两块数据，都还存在
            while (left <= (start + end) / 2 && right <= end) {
                //比较两块数据的大小，然后赋值，并且移动下标
                if (arr[left] <= arr[right]) {
                    result[index] = arr[left];
                    left++;
                } else {
                    result[index] = arr[right];
                    right++;
                }
                //移动单位记录的下标
                index++;
            }
            //当某一块数据不存在了时
            while (left <= (start + end) / 2 || right <= end) {
                //直接赋值到记录下标
                if (left <= (start + end) / 2) {
                    result[index] = arr[left];
                    left++;
                } else {
                    result[index] = arr[right];
                    right++;
                }
                index++;
            }
            //最后将新的数据赋值给原来的列表，并且是对应分块后的下标。
            for (int i = start; i <= end; i++) {
                arr[i] = result[i - start];
            }
        }
    }