递归核心思想 总结
最后总结
其实，递归不一定总是从上往下，也是有很多是从下往上的，例如 n = 1 开始，一直递归到 n = 1000，例如一些排序组合。对于这种从下往上的，也是有对应的优化技巧，不过，我就先不写了，后面再慢慢写。这篇文章写了很久了，脖子有点受不了了，，，，颈椎病？害怕。。。。
说实话，对于递归这种比较抽象的思想，要把他讲明白，特别是讲给初学者听，还是挺难的，这也是我这篇文章用了很长时间的原因，不过，只要能让你们看完，有所收获，我觉得值得！
另外，我正在整理一份计算机类书单，只为让大家更加方便找到自己想要的书籍，目前已经收集了几百本了，贡献给需要的人：计算机的书籍很贵？史上最全计算机类电子书整理（持续更新），截图了部分数据结构与算法的书籍如下：
链表的重要性不言而喻，如果你把我分享的这10道题都搞懂了，那么你在链表方面算过关的了：
【链表问题】如何优雅着反转单链表mp.weixin.qq.com
就不一道道列出来了，一共挑选了10还不错的文章
十道链表打卡汇总mp.weixin.qq.com
我还讲解了一些常用数据结构与算法思想，每篇都通俗易懂着讲解了，被各种号所转发
1、十大排序重要性不言而喻，文章还附带了动画、讲解文章，代码
必学十大经典排序算法，看这篇就够了(附完整代码/动图/优质文章)(修订版)mp.weixin.qq.com
2、总结了刷题过程中常用的技巧，推荐阅读：
一些常用的算法技巧总结mp.weixin.qq.com
3、用漫画的形式讲解了AVL树：
【漫画】以后在有面试官问你AVL树，你就把这篇文章扔给他。mp.weixin.qq.com
4、大量图讲解了堆的各种操作：
【算法与数据结构】堆排序是什么鬼？mp.weixin.qq.com
索性把写的一些文章链接都分享一波，大家可以挑感兴趣的看
算法与数据结构系列文章---------------------------------干货整理-------------------------------------------
另外，我正在整理一份计算机类书单，只为让大家更加方便找到自己想要的书籍，目前已经收集了几百本了，贡献给需要的人：
iamshuaidi/CS-Bookgithub.com
部分书籍截图
如果你觉得这篇内容对你挺有启发，我想邀请你帮我三个忙，让更多的人看到这篇文章：
递归要和迭代比较来看。
迭代是重复反馈过程的活动，其目的通常是为了逼近所需目标或结果。每一次对过程的重复称为一次“迭代”，而每一次迭代得到的结果会作为下一次迭代的初始值，因此迭代是从前往后计算的。
递归则是一步一步往前递推，直到递归基础，寻找一条路径， 然后再由前向后计算。
迭代是从前往后计算的，而递归则是先从后往前推，然后再由前往后计算，有“递”又有“归”。
通俗来讲：引自@lishichengyan
一个小朋友坐在第10排，他的作业本被小组长扔到了第1排，小朋友要拿回他的作业本，可以怎么办？
他可以拍拍第9排小朋友，说“帮我拿第1排的本子”，而第9排的小朋友可以拍拍第8排小朋友，说“帮我拿第1排的本子”...如此下去，消息终于传到了第1排小朋友那里，于是他把本子递给第2排，第2排又递给第3排...终于，本子到手啦！
这就是递归，拍拍小朋友的背可以类比函数调用，而小朋友们都记得要传消息、送本子，是因为他们有记忆力，这可以类比栈。
更严谨一些，递归蕴含的思想其实是数学归纳法：为了求解问题p（n），首先解决基础情形p（1），然后假定p（n-1）已经解决，在此基础上若p（n）得解，那所有问题均得解。
递归三要素
递归的定义：接受什么参数，返回什么值，代表什么意思 。当函数直接或者间接调⽤⾃⼰时，则发⽣了递归
递归的拆解：每次递归都是为了让问题规模变⼩
递归的出⼝：必须有⼀个明确的结束条件。因为递归就是有“递”有“归”，所以必须又有一个明确的点，到了这个点，就不用“递下去”，而是开始“归来”。
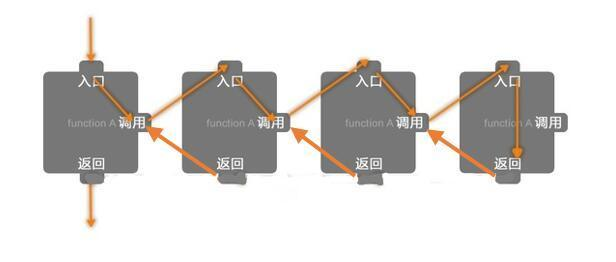递归的过程
下面这个求 n! 的例子中，递归出口（确定递归什么时候结束）是fun(1)=1，递归体（确定递归求解时的递归关系）是fun(n)=n*fun(n-1)，n>1。
int fun(int n){ if(n==1) return 1; else return n*fun(n-1); }
递归一般用在可能无限循环下去的操作里，举个例子，像电脑里的文件夹系统，打开一个文件夹，里面有很多的文件或文件夹，里面这些文件夹又可以打开，然后重复上面的过程，你是不知道你在什么位置结束这个循环的。
所以你不能按顺序一句句代码的写下去，因为你根本不知道什么时候结束。这怎么办？
用到递归的时候，基本上我们想要进行操作都是由一个简单的小操作重复完成的（实际上是这样的环境时才用递归），那这是就可以写一个函数来完成这个小操作然后循环就可以了。
比如有个需求，你要计算一个文件夹里总共有多少个文件，这里的操作单元就是：一个文件夹只计算它下一级的文件数，不用去管它的子文件夹的子文件夹等等更下一层的情况。这样每个文件夹把它下一级的文件数统计上来，它自身的文件数就是对的。
或者举个更生活的例子，学校要统计去参加XX活动的人数，从上至下是学校->院系->专业->年级->班,虽然有很多层,但是对于系里面来说，它只要把专业统计的人员加起来就可以了，不用去管年级、班级的人数，其他层也是一样，它只管它下一级的人数。
所以我觉得很重要的是怎么把一个任务合理的拆分成可以重复的单元，然后函数本身只要实现这个重复的这段操作就可以了。
这个和数学里面一个证明方法很像，方法思路大概是：
1.参数为0的时候是正确的
2.假如参数为n的时候是正确的，可以得出n+1的时候是正确的 ，
满足这两个条件，那么对于任何参数都是正确的。
这个过程是开始是固定的，但是没有结尾，是从开始想远处推倒。
递归呢，是整个过程有一个结尾，比如文件夹一直打开最后你肯定会遇到一个空文件夹或者全部是文件的文件夹，循环终止，是一个从任意处向终点推倒的过程。函数完成后的效果肯定是你选择任意一个文件夹，它都可以计算出总共的文件数，所以看似是起点已知，但实际起点是任意的。
贴个示例代码：//文件 struct file { char* name; }; //文件夹 struct folder{ struct folder* subfolders; int folderNum; struct file* files; int fileNum; }; int countFiles(struct folder fol) { int num = fol.fileNum; //循环子文件夹，把文件数加起来 for (int i = 0; i< fol.folderNum; ++i) { struct folder subFolder = fol.subfolders[i]; num += countFiles(subFolder); //在这个位置形成递归；但是你要计算的是fol的数量，你只需要直接使用subFolder的数量 //就像是接力赛，你要相信对subFolder的计算式正确的，在这个基础上计算当前这个层级数量 } return num; }
