2020icpc济南 - A

组合数学 + 高斯消元

[A-Matrix Equation_第 45 届国际大学生程序设计竞赛（ICPC）亚洲区域赛（济南） (nowcoder.com)](https://codeforces.com/problemset/problem/1632/D)

题意

给出两个大小为 $n\;(1<=n<=200)$ 的矩阵 A，B （A，B个元素都是 0 或 1）。求矩阵 $C$ 的方案数，满足 A，C的矩阵乘法 %2 == A，C 的对应位置的相乘

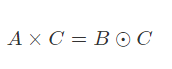
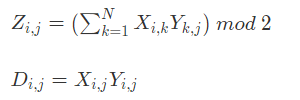
思路

1. C 的各列是独立的，求出每一列的方案数相乘即可
2. 对于 C 的某一列，分别设为 [x1, x2, x3 ... ,xn], 带入等式即可得到一个异或方程组，高斯消元求出自由元个数 cnt，这一列的方案就是 $2^{cnt}$
3. 用 bitset 优化

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <bitset>
using namespace std;
#define endl "\n"

typedef long long ll;
typedef pair<int, int> PII;

const int N = 210;
const int mod = 998244353;
int n;
int A[N][N], B[N][N];

bitset<N> a[N];

ll qmi(ll a, ll b)
{
	ll ans = 1;
	while(b)
	{
		if (b & 1)
			ans = ans * a % mod;
		b >>= 1;
		a = a * a % mod;
	}
	return ans;
}

int guess()
{
	int r, c;
	for (c = 1, r = 1; c <= n; c++)
	{
		int t = r;
		for (int i = r; i <= n; i++)
			if (a[i][c] > a[t][c]) t = i;
		if (a[t][c] == 0)
			continue;
		swap(a[r], a[t]);
		for (int i = r + 1; i <= n; i++)
		{
			if (a[i][c] == 1)
				a[i] ^= a[r];
		}
		r++;
	}
	r--;
	return n - r;
}

ll solve(int p)
{
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= n; j++)
			a[i][j] = A[i][j];
	for (int i = 1; i <= n; i++)
	{
		int x = A[i][i] - B[i][p];
		if (x < 0) x += 2;
		a[i][i] = x;
	}
	int cnt = guess();
	return qmi(2, cnt);
}
int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= n; j++)
			scanf("%d", &A[i][j]);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= n; j++)
			scanf("%d", &B[i][j]);
	ll ans = 1;
	for (int i = 1; i <= n; i++)
		ans = ans * solve(i) % mod;
	printf("%lld\n", ans);
    return 0;
}