ABC263 F - Tournament

DP + 优化转移

F - Tournament (atcoder.jp)

题意

有 \(2^n\;(n<=16)\) 个人排成一排，第 1，2 个进行比赛，第3，4 个进行比赛 . . . 第 \(2^n-1\) 个与 第 \(2^n\) 个进行比赛，输掉的被移除，下一轮则是剩下 \(2^{n-1}\) 个人重复之前操作，直到只剩一个人

有一个 \(2^n*n\) 的矩阵 C，\(C[i][j]\) 表示第 i 个人赢了 j 场的分数，若可以任意决定每场比赛的结果，求这 \(2^n\) 个人的分数和最大

思路

考虑在二叉树中进行DP

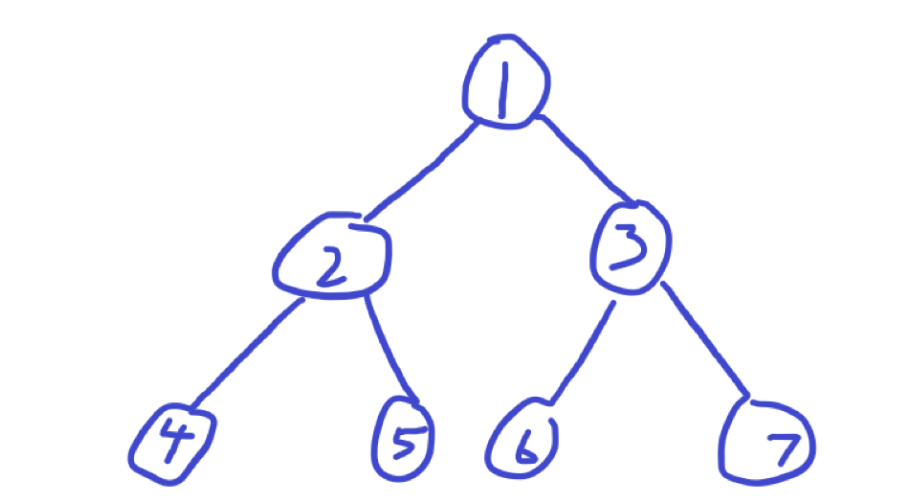
本来考虑的是 \(f[u]\) 表示 u 子树中的最大分数和，但是 u 子树中胜出的那个人对之后还是有影响的，所以有后效性，要用 \(f[u][id]\) 表示 u 子树中第 id 个人胜出了，此时的最大分数和

这样共有 \(1*2^n+2*2^{n-1}+4*2^{n-2}+...+2^n=n*2^n\) 个状态

转移

对于每个结点 u，遍历他所包含的叶子结点编号 i，i 作为这个子树的胜者

1. i 在 u 的左子树中, 设从叶子到 u 要赢 k 场（k 可由 u 的深度求出）

   ·答案由 i 赢到左儿子时左儿子的贡献 + i 赢 k 把的贡献 - i 赢 k - 1 把的贡献 + 右儿子无论谁赢的贡献最大值（反正都要被左儿子出来的 i 打败）

   \(f[u][i]=f[lson][i]+C[i][k]-C[i][k-1]+max(f[rson][j])\)

   其中 \(max(f[lson][i])\) 可以再用 maxn[u] 表示 u 子树的最大值 dp 出来

2. i 在 u 的右子树，同理

注意若每个结点第二维都开 \(2^n\) 则空间不足，要根据它实际的叶子数开，或者滚动数组优化

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
using namespace std;
#define endl "\n"
typedef long long ll;
typedef pair<int, int> PII;

const int N = 17;
vector<vector<ll> > f(1 << N);
int l[1 << N];
ll c[1 << N][N];
ll maxn[1 << N];
int n;
 
void dp(int u)
{
	int h = __lg(u) + 1;
	int k = n + 1 - h;
	if (k == 0)
	{
		l[u] = u % (1 << n) + 1;
		return;
	}
	dp(u << 1);
	dp(u << 1 | 1);
	int sz = 1 << k - 1;
	l[u] = l[u << 1];
	int L = l[u] - 1;
	for (int i = 1; i <= sz; i++)
	{
		f[u][i] = f[u << 1][i] - c[L + i][k - 1] + c[L + i][k] + maxn[u << 1 | 1];
		f[u][sz + i] = f[u << 1 | 1][i] - c[L + sz + i][k - 1] + c[L + sz + i][k] + maxn[u << 1];
		maxn[u] = max({maxn[u], f[u][i], f[u][sz + i]});
	}
}
int main()
{
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin >> n;
	for (int i = 1; i < 1 << n; i++)
	{
		int h = n - (int)__lg(i);
		f[i].resize((1 << h) + 2, 0);
	}
	for (int i = 1 << n; i < 1 << n + 1; i++)
		f[i].resize(2, 0);
	for (int i = 1; i <= 1 << n; i++)
		for (int j = 1; j <= n; j++)
			cin >> c[i][j];
	dp(1);
	cout << maxn[1] << endl;

    return 0;
}