CF Round#787（div3） F - Vlad and Unfinished Business

F - Vlad and Unfinished Business

树形dp

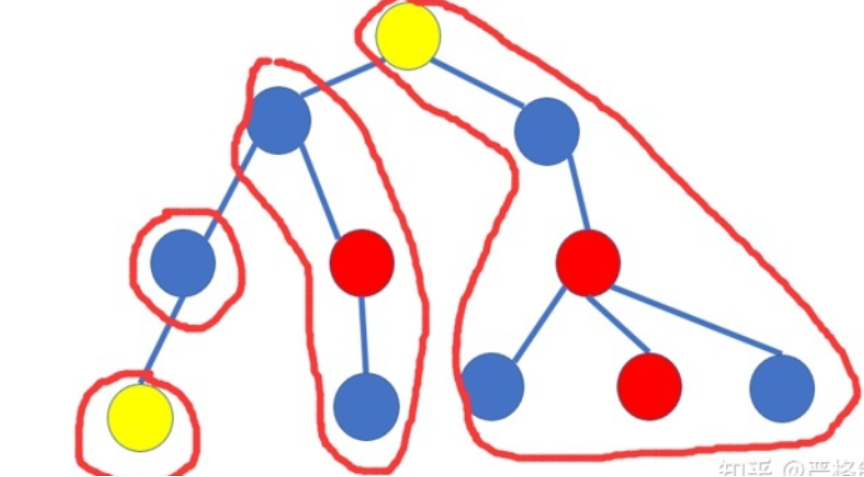
答案可看作是 x->y 路径长度 + 路径上的点向有标记的点上拐一圈回来的代价

1. 先以 x 为根 dfs，求出将路径上的点 $u$ 标记为 $path[u]=1$, $son[u]$ 表示 $u$ 子树中的标记个数
2. 从 x -> y 的每个结点 dfs2 一次 (dfs2(u) 表示从 u 向旁边路径拐一下的代价)，设当前路径上的点为 $u$, 若 $u$ 的儿子 $v$ 中有特殊点，就要往 $v$ 拐一下，答案加上 $dfs2(v)+2$

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>

using namespace std;
#define endl "\n"

typedef long long ll;
typedef pair<int, int> PII;

const int N = 2e5 + 10;
int n, k, x, y;
int a[N];
int path[N], son[N];
vector<vector<int> > G(N);
void add(int u, int v)
{
	G[u].push_back(v);
}

void dfs(int u, int fa)
{
	for (int v : G[u])
	{
		if (v == fa)
			continue;
		dfs(v, u);
		son[u] += son[v];
		path[u] |= path[v];
	}
}

ll dfs2(int u, int fa)
{
	ll ans = 0;
	for (int v : G[u])
	{
		if (v == fa)
			continue;
		if (!path[v] && son[v])
			ans += dfs2(v, u) + 2;
	}
	return ans;
}

void init()
{
	for (int i = 1; i <= n; i++)
	{
		G[i].clear();
		son[i] = 0;
		path[i] = 0;
	}
}
int main()
{
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int T;
	cin >> T;
	while(T--)
	{
		cin >> n >> k;
		cin >> x >> y;
		init();
		path[y] = 1;
		for (int i = 1; i <= k; i++)
		{
			cin >> a[i];
			son[a[i]] = 1;
		}
		for (int i = 1; i < n; i++)
		{
			int u, v;
			cin >> u >> v;
			add(u, v), add(v, u);
		}
		dfs(x, -1);
		ll ans = 0;
		for (int u = 1; u <= n; u++)
		{
			if (path[u])
				ans += dfs2(u, -1);
		}
		ans += count(path + 1, path + n + 1, 1) - 1;
		cout << ans << endl;
	}
    return 0;
}