积性函数

常见积性函数

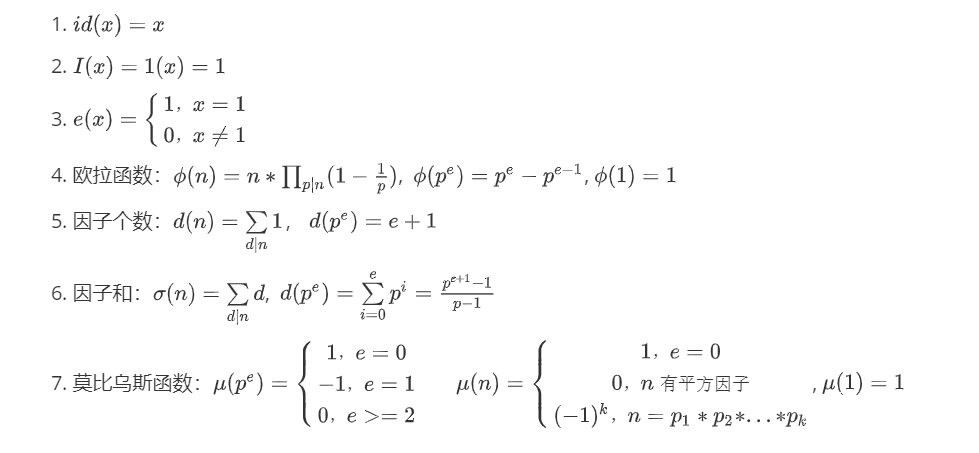
线性筛求常见积性函数

设 $f(n)$ 为积性函数

$n=p_1^{e_1}*p_2^{e_2}*p_3^{e_3}*...p_k^{e_k}$, 设 $p_1$ 为最小素因子

由积性函数性质，$f(n) = f(\frac n{p_1^{e_1}})*f(p_1^{e_1})$

若 $n=p^e$, 即 $n$ 为素数幂的形式

设则由积性函数自身的性质而定，例如：

1. $d(p^e)=d(p^{e-1})+1$

2. $\sigma(p^e)=\sigma(p^{e-1})+p^e$

3. $\phi(p^e)=p^e-p^{e-1}$

4. $\mu(p^e)=1,\;e=1$

   $\mu(p^e)=0,\;e>2$

在线性筛中计算出 $i$ 的最小素因子 $p[i]$ 与 $i$ 的最小素因子的最高次幂 $pe[i]$ 可完成上述递推

常见积性函数 - 题目 - Daimayuan Online Judge

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>

using namespace std;
typedef long long ll;
typedef unsigned int uint;
const int N = 2e7 + 10;
uint n, a, b, cnt;
uint pr[N/5], p[N], pe[N], d[N], sigma[N], phi[N], mu[N];
void get_primes(int n)
{
	p[1] = 1;
	for (int i = 2; i <= n; i++)
	{
		if (!p[i])
		{
			p[i] = i;
			pr[++cnt] = i;
			pe[i] = i;
		}
		for (int j = 1; j <= cnt && pr[j] <= n / i; j++)
		{
			p[i*pr[j]] = pr[j];
			if (p[i] == pr[j])
			{
				pe[i*pr[j]] = pe[i] * pr[j];
				break;
			}
			pe[i*pr[j]] = pr[j];
		}
	}
}

void presolve(int n)
{
	d[1] = sigma[1] = phi[1] = mu[1] = 1;
	for (int i = 2; i <= n; i++)
	{
		if (pe[i] != i)
		{
			d[i] = d[i/pe[i]] * d[pe[i]];
			sigma[i] = sigma[i/pe[i]] * sigma[pe[i]];
			phi[i] = phi[i/pe[i]] * phi[pe[i]];
			mu[i] = mu[i/pe[i]] * mu[pe[i]];
		}
		else
		{
			d[i] = d[i/p[i]] + 1;
			sigma[i] = sigma[i/p[i]] + i;
			phi[i] = i / p[i] * (p[i] - 1);
			mu[i] = (i == p[i] ? -1 : 0);
		}
	}
}
int main()
{
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	cin >> n >> a >> b;
	get_primes(n);
	presolve(n);
	uint d_sum = 0, sigma_sum = 0, phi_sum = 0, mu_sum = 0;
	for (int i = 1; i <= n; i++)
	{
		d_sum ^= a * i * d[i] + b;
		sigma_sum ^= a * i * sigma[i] + b;
		phi_sum ^= a * i * phi[i] + b;
		mu_sum ^= a * i * mu[i] + b;
	}
	cout << d_sum << endl;
	cout << sigma_sum << endl;
	cout << phi_sum << endl;
	cout << mu_sum << endl;
	return 0;
}