欧拉定理

欧拉定理

欧拉定理

​ \(gcd(a,m)=1\) 时， \(a^{x}\equiv a^{x \mod \phi(m)}\;(mod\;m)\)

扩展欧拉定理：

​ \(a^{x}\equiv a^{x \mod \phi(m)+\phi(m)}\;(mod\;m)\)

证明：

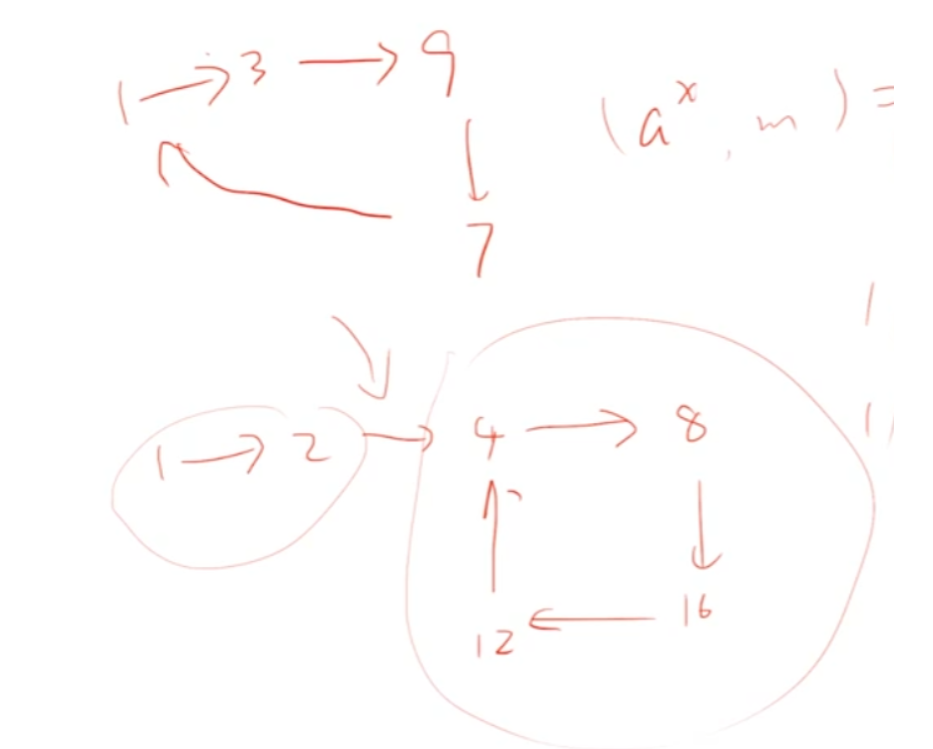
a 与 m 互质时，从 \(a_0\) 就进入循环

a 与 m 不互质时，从前 c 项不进入循环，设循环长度为 L

设已经走了 x 步，则 x = L + x - L 所以先走 L 步进入循环，这时再走 x - L 步的位置与再走 (x - L) % L 一样，因此有

​ (L + (x - L) % L) = L + x % L, 即 \(a^{x}\equiv a^{x \mod \phi(m)+\phi(m)}\;(mod\;m)\)

BZOJ 3884, 上帝与集合的正确用法 - 题目 - Daimayuan Online Judge

\(\phi (m)\) 的性质

1. \(\phi(m)\) 为偶数（除 m = 2 外）

2. \(\phi(m)<=\frac m2\)

因此只需 log p 次就可将 p 减为 1，因此只需递归子问题 log p 次即可

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>

using namespace std;
typedef long long ll;

ll qmi(ll a, ll b, ll p)
{
	ll ans = 1;
	while(b)
	{
		if (b & 1)
			ans = ans * a % p;
		a = a * a % p;
		b >>= 1;
	}
	return ans % p;
}
//递归子问题求解
ll calc(int p)
{
	if (p == 1)
		return 0;
	ll phip = p, now = p;
	for (int i = 2; i <= now / i; i++)
	{
		if (now % i) continue;
		phip = phip / i * (i - 1);
		while(now % i == 0) now /= i;
	}
	if (now > 1) phip = phip / now * (now - 1);
	ll ans = calc(phip);
	return qmi(2, ans + phip, p);
}
ll solve()
{
	int p;
	cin >> p;
	return calc(p);
}
int main()
{
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	int T;
	cin >> T;
	while(T--)
		cout << solve() << endl;
	return 0;
}

CF Round #454(Div 1) D, Power Tower - 题目 - Daimayuan Online Judge

使用扩展欧拉定理降幂时，重定义 mod 运算为

ll mod(ll a, ll b)
{
	if (a < b) return a;
	return a % b + b;
}

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <map>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
ll a[N];
map<ll, ll> mp;
//使用扩展欧拉定理时要重定义mod
ll mod(ll a, ll b)
{
	if (a < b) return a;
	return a % b + b;
}

ll qmi(ll a, ll b, ll p)
{
	ll ans = 1;
	while(b)
	{
		if (b & 1)
			ans = mod(ans * a, p);
		b >>= 1;
		a = mod(a * a, p);
	}
	return mod(ans, p);
}

ll phi(ll x)
{
	if (mp[x]) return mp[x];
	ll now = x, ans = x;
	for (int i = 2; i <= now / i; i++)
	{
		if (now % i == 0)
			ans -= ans / i;
		while(now % i == 0)
			now /= i;
	}
	if (now > 1)
		ans -= ans / now;
	return mp[x] = ans;
}

ll solve(int l, int r, int p)
{
	if (p == 1 || l == r) return mod(a[l], p);
	return qmi(a[l], solve(l+1, r, phi(p)), p);
}
int main()
{
	int n, m, q;
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++)
		scanf("%lld", a + i);
	scanf("%d", &q);
	while(q--)
	{
		int l, r;
		scanf("%d%d", &l, &r);
		printf("%lld\n", solve(l, r, m) % m);
	}
		
	return 0;
}