CF EDU 113 D - Inconvenient Pairs

D - Inconvenient Pairs

思维

不方便的点对就是类似于，这种在同一行块或同一列块的两个点，他们的距离一定大于曼哈顿距离

其中红色为横向点对，紫色为纵向点对

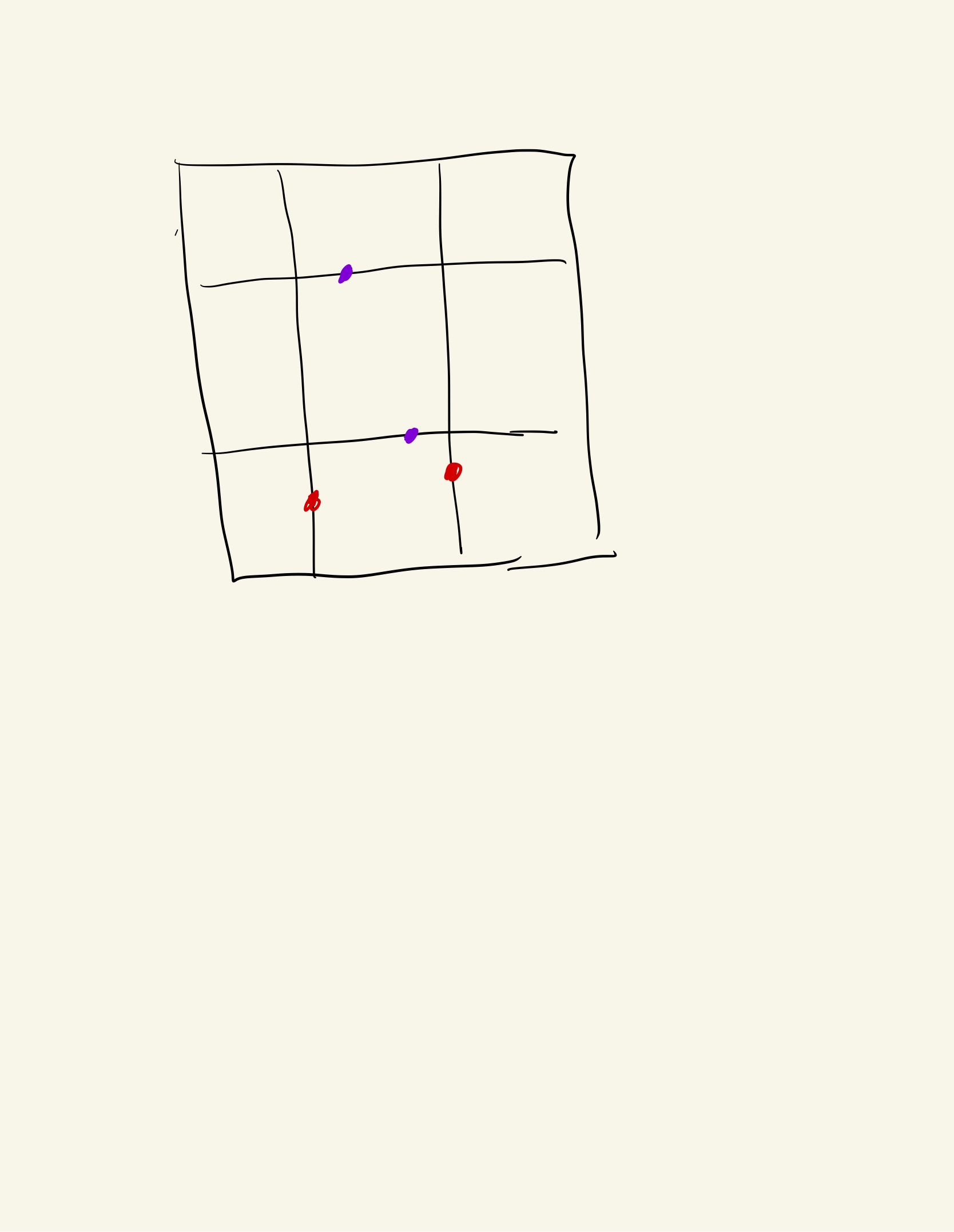
所以可按 y 递增排序，找到每一个行块有多少个点，这一行块中的点对贡献为：\(\binom {cnt}2-\sum\binom {同一列的点的数量}2\)

注意当某个点的 y 就是行块分割的线时，它和任何点都不会构成 “横向” 的点对，所以可以一开始读入的时候记录下来，枚举到这个点就continue

求 “纵向” 点对数目同理

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <map>

using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 3e5 + 10;
int n, m, k;
int row[N], col[N];
map<int, int> xcnt, ycnt;
map<int, bool> xban, yban;
struct Point
{
	int x, y;
}p[N];

bool cmp1(Point A, Point B)
{
	if (A.x == B.x)
		return A.y < B.y;
	return A.x < B.x;
}

bool cmp2(Point A, Point B)
{
	if (A.y == B.y)
		return A.x < B.x;
	return A.y < B.y;
}

void init()
{
	xcnt.clear();
	ycnt.clear();
	xban.clear();
	yban.clear();
}
int main()
{
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	int T;
	cin >> T;
	while(T--)
	{
		cin >> n >> m >> k;
		init();
		for (int i = 1; i <= n; i++)
		{
			cin >> col[i];
			xban[col[i]] = true;
		}
			
		for (int i = 1; i <= m; i++)
		{
			cin >> row[i];
			yban[row[i]] = true;
		}
			
		for (int i = 1; i <= k; i++)
			cin >> p[i].x >> p[i].y;
		sort(p + 1, p + k + 1, cmp2);
		int id = 2;
		ll ans = 0;
		for (int i = 1; i <= k; i++)
		{
			int x = p[i].x, y = p[i].y;
			if (yban[y])
				continue;
			if (y > row[id])
			{
				ll add = 0, sum = 0;
				for (auto t : xcnt)
				{
					sum += t.second;
					add -= t.second * (t.second - 1) / 2;
				}
				add += sum * (sum - 1) / 2;
				ans += add;
				xcnt.clear();
				while(y > row[id]) id++;
			}
			xcnt[x]++;
		}
		if (xcnt.size())
		{
			
			ll add = 0, sum = 0;
			for (auto t : xcnt)
			{
				sum += t.second;
				add -= t.second * (t.second - 1) / 2;
			}
			add += sum * (sum - 1) / 2;
			ans += add;
			xcnt.clear();
		}
		sort(p + 1, p + k + 1, cmp1);
		id = 2;
		for (int i = 1; i <= k; i++)
		{
			int x = p[i].x, y = p[i].y;
			if (xban[x])
				continue;
			if (x > col[id])
			{
				ll add = 0, sum = 0;
				for (auto t : ycnt)
				{
					sum += t.second;
					add -= t.second * (t.second - 1) / 2;
				}
				add += sum * (sum - 1) / 2;
				ans += add;
				ycnt.clear();
				while(x > col[id]) id++;
			}
			ycnt[y]++;
		}
		if (ycnt.size())
		{
			ll add = 0, sum = 0;
			for (auto t : ycnt)
			{
				sum += t.second;
				add -= t.second * (t.second - 1) / 2;
			}
			add += sum * (sum - 1) / 2;
			ans += add;
			ycnt.clear();
		}
		cout << ans << endl;
	}
	return 0;
}