【题解】ABC186F Rook on Grid（线段树）

有一个 \(n\times m\) 的网格棋盘，第 \(i\) 行 \(j\) 列网格的坐标为 \((i,j)\)。

网格上有 \(k\) 个障碍物。

现在从棋盘左上角有一颗象棋“车”（行走方式为每一步走直线，且不能碰到或越过障碍）。

求车在至多走 \(2\) 步的情况下，能够到达的网格数量。

\(n,m,k\le 2\times 10^5\)，所有障碍物的坐标均在网格内，且 \((1,1)\) 位置没有障碍。

题解

我们发现，因为车只能从 \((1, 1)\) 出发走至多 \(2\) 步。因此对于一个格子，可能到达它的路径只有下图中的红蓝两种：

考虑一行，我们将从这行开头向右可以到达的格子成为红色格子，其他的格子称为蓝色格子，如下图。

其中红色格子是只能先下后右到达的，蓝色格子则是只能先右后下。（不一定所有的红/蓝色格子都可以到达）

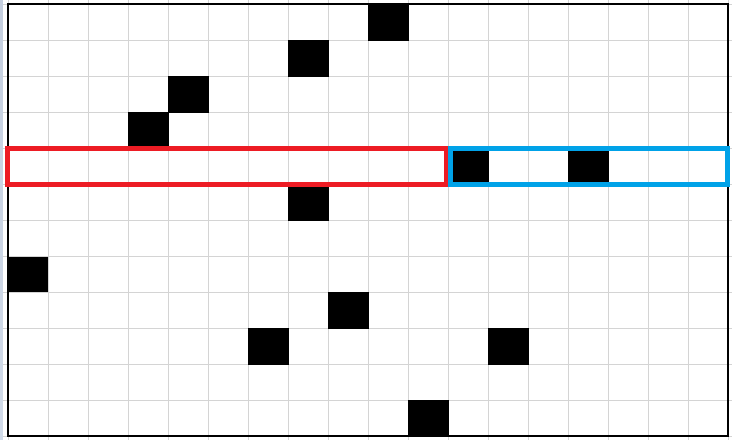
我们称一个格子合法，就是指这个格子可以通过两步移动到达 \((1, 1)\)。答案即为 合法的红色格子 \(+\) 合法的蓝色格子。

我们从上往下遍历每一行，考虑计算每一行的贡献。

首先计算红色格子，我们只需要将每一行的障碍的 \(y\) 放进这一行的 \(vector\) 里面排序，就可以快速求出最左边的障碍位置。

但是需要注意，如果当前行的第一个格子不合法，也就是说从它向上到 \((1,1)\) 的路径要经过障碍，那么当前行其实不存在红色格子。这个也好处理，从上往下遍历的时候记录一个标记即可。

然后考虑计算蓝色格子，蓝色格子的路径是先右再下，所以我们可以考虑用线段树来记录当前行的所有格子能否作为合法的蓝色格子。（注意，这里的合法是指的能否从 \((1, 1)\) 先右再下到达）

对于当前行，直接暴力将障碍位置标记为不合法，对于之后的行，这些障碍所在的列同样不合法，所以不用撤销标记。

需要注意第一行最左侧的障碍，因为这个障碍及其右边的列必须提前标记为不合法（因为这些列不能作为合法的蓝色格子）。

对于当前行，合法的蓝色格子数量用线段树查询 \([最左侧障碍的y,m]\) 中合法标记数量即可。

需要线段树区间覆盖、询问区间和。时间复杂度 \(O((k+m)\log{m})\)。

点击查看代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

const int N = 2E5 + 5;

int n, m, k;
vector<int> x[N];
int sum[N * 4], tag[N * 4];

#define lson (rt << 1)
#define rson (rt << 1 | 1)
#define mid ((l + r) / 2)
void push_down(int rt, int l, int r) {
	if(tag[rt] != -1) {
		tag[lson] = tag[rson] = tag[rt];
		sum[lson] = tag[rt] * (mid - l + 1);
		sum[rson] = tag[rt] * (r - mid);
		tag[rt] = -1;
	}
}
void update(int rt, int l, int r, int L, int R, int val) {
	if(L <= l && r <= R) {
		tag[rt] = val;
		sum[rt] = (r - l + 1) * val;
		return;
	}
	push_down(rt, l, r);
	if(L <= mid) {
		update(lson, l, mid, L, R, val);
	}
	if(R > mid) {
		update(rson, mid + 1, r, L, R, val);
	}
	sum[rt] = sum[lson] + sum[rson];
}
int query(int rt, int l, int r, int L, int R) {
	if(L <= l && r <= R) {
		return sum[rt];
	}
	push_down(rt, l, r);
	int res = 0;
	if(L <= mid) {
		res += query(lson, l, mid, L, R);
	}
	if(R > mid) {
		res += query(rson, mid + 1, r, L, R);
	}
	return res;
}
#undef lson
#undef rson
#undef mid

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	
	cin >> n >> m >> k;
	for(int i = 1; i <= k; ++i) {
		int X, Y;
		cin >> X >> Y;
		x[X].emplace_back(Y);
	}
	for(int i = 1; i <= n; ++i) {
		sort(x[i].begin(), x[i].end()); // 每一行有序 
	}
	
	memset(tag, -1, sizeof(tag));
	
	i64 ans = 0, f = 1; // f表示当前行第一格是否可以直接向上走 
	update(1, 1, m, 1, m, 1); // 先赋值为全部合法
	if(x[1].size()) {
		update(1, 1, m, x[1][0], m, 0); // 第一行不能向右走到列直接不合法 
	} 
	for(int i = 1; i <= n; ++i) {
		for(auto y : x[i]) {
			update(1, 1, m, y, y, 0); // 更新蓝色部分合法性 
		}
		
		if(x[i].size() && x[i][0] == 1) {
			f = 0;
		}
		
		if(x[i].size()) {
			if(f) {
				ans += x[i][0] - 1;
				ans += query(1, 1, m, x[i][0], m);
			} else {
				ans += query(1, 1, m, 1, m);
			}
		} else {
			if(f) {
				ans += m;
			} else {
				ans += query(1, 1, m, 1, m);
			}
		}
	}
	
	cout << ans << "\n";
	
	return 0;
}