20172302 《Java软件结构与数据结构》第一周学习总结
2018下半年学习总结博客总目录:[第一周](https://www.cnblogs.com/hzy0628/p/9606767.html)
教材学习内容总结
第一章 概述
1.软件质量
软件工程(Software Engineering)是一门关于高质量软件开发的技术和理论的学科。
软件质量从以下八个方面进行考虑:
- 正确性 按照需求规范所规定的那样处理问题,在很大程度上满足其特定需求
- 一、程序语法错误。
- 二、程序对于几组输入数据能够得出满足需要的结果。
- 三、程序对于精心选择的、典型、苛刻切带有***难性的几组输入数据能够得出满足要求的结果。
- 四、程序对于一切合法的输入数据都能得到满足要求的结果。
- 可靠性 应尽可能减少发生故障的频率,同时降低发生故障时所造成的损失
- 健壮性 在异常的状态能够对异常进行处理,而非发生异常就造成终止 。当输入的数据非法时,算法应当恰当的做出反应或进行相应处理,而不是产生莫名其妙的输出结果。并且,处理出错的方法不应是中断程序执行,而是应当返回一个表示错误或错误性质的值,以便在更高的抽象层次上进行处理。
- 可用性 软件的使用过程中的难易程度
- 可维护性 对软件部分代码进行修改的难易程度
- 可重用性 软件组件可重用于其他软件系统开发的难易程度
- 可移植性 软件组件在不同计算机环境下使用的难易程度
- 运行效率 在不浪费资源的情况下软件完成其目标的程度
2.数据结构
数据结构:把多个数据按照一定的存储方式,存储起来,称存储方式之为数据结构.
数据的存储方式有很多,数组,队列,链表,栈,哈希表等等. 不同的数据结构,性能是不一样的,比如有的插入比较快,查询比较快,但是删除比较慢. 有的删除比较快,插入比较快,但是查询比较慢. 根据实际操作,合理选择即可.

不同数据结构之间比较
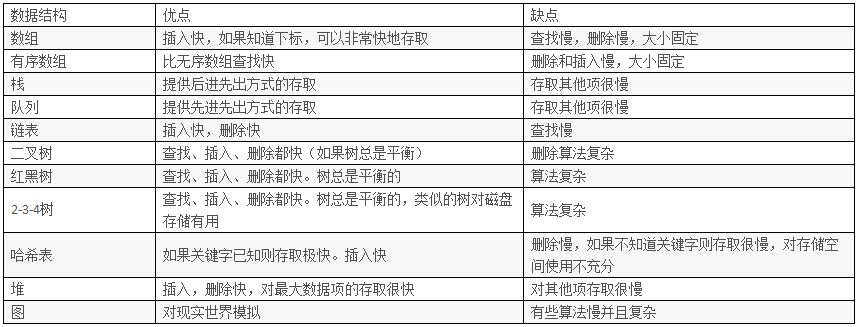
第二章 算法分析
算法分析(analysis of algorithm)是计算机科学的基础,它是从效率角度对算法进行分类。
算法效率通常用CPU的使用时间来表示。
增长函数与大O记法
-
增长函数是表示问题(n)大小与我们希望最优化的值之间的关系,该函数表示了该算法的时间复杂度或空间复杂度。
-
渐进复杂度(asymptotic complexity)称为算法的阶次,随着问题大小的增加时增长函数的一般性质,这一性质取决于该表达式的主项,即n增加时表达式中增长最快的那一项。
-
大O记法:我们将算法具有阶次为n的时间复杂度,记为O(n)。

增长函数的比较
- 在给定时间内系统所能处理的最大问题,我们将处理器的速度提高10倍,这时再有系统所能处理的最大问题,见下表
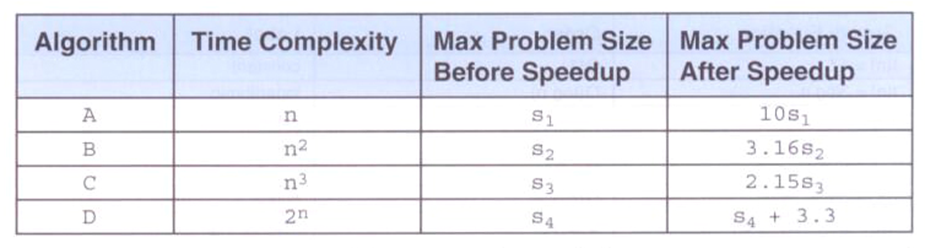
-
各种增长函数之间的比较
- n 较小时

- n 较大时
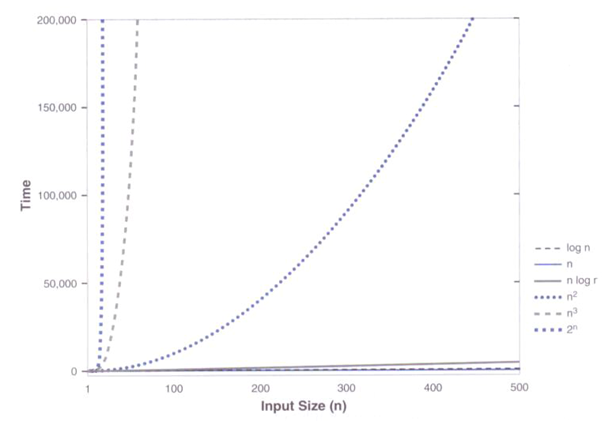
- n 较小时
-
结论:c(常量)<㏒₂n < n < n㏒₂n < n²< n³ < 2ⁿ < 3ⁿ< n!
时间复杂度分析
- 1.循环运行的复杂度分析
首先确定循环体的阶n,然后乘以循环执行的次数
for (int count = 0; count < n; count++)
{
// 复杂度为O(1)的步骤系列
}
n * O(1) →O(n)
- 2.嵌套循环的复杂度分析
循环出现嵌套时,循环的复杂度等于内层循环的复杂度乘以外层循环的复杂度
for (int count = 0; count < n; count++)
for (int count2 = 0; count2 < n; count2++)
{
//复杂度为O(1)步骤系列
}
内外层循环的复杂度均为O(n),整体的复杂度为O(n²)
- 3.方法调用的复杂度分析
循环体可能包含方法的调用,要确定循环体的阶,需要考虑调用方法的阶
for (int count=0 ; count<n; count++)
{
Printsum(count);
}
以下是Printsum方法
Public void printsum(int count)
{
Int sum =0;
for(int i=0; i<count; i++)
sum += i;
System.out.println(sum);
}
于是整体的复杂度为O(n²)
时间复杂度的计算规则
-
- 加法规则
T(n,m) = T1(n) + T2(n) = O (max ( f(n), g(m) )
- 加法规则
-
- 乘法规则
T(n,m) = T1(n) * T2(m) = O (f(n) * g(m))
- 乘法规则
-
- 一个特例(问题规模为常量的时间复杂度)
在大O表示法里面有一个特例,如果T1(n) = O(c), c是一个与n无关的任意常数,T2(n) = O ( f(n) ) 则有T(n) = T1(n) * T2(n) = O ( c*f(n) ) = O( f(n) )。也就是说,在大O表示法中,任何非0正常数都属于同一数量级,记为O(1)。
- 一个特例(问题规模为常量的时间复杂度)
教材学习中的问题和解决过程
-
可靠性与健壮性之间的关系是什么?
-
可靠性关注的是软件发生故障的频率以及在什么环境下发生故障,而健壮性关注的是软件系统出现故障会发生什么?
系统的健壮性(robustness)也称为系统的坚固性或坚实性,这是衡量一个系统能否从各种出错条件下恢复能力的一种测度。引起出错的条件可以是来自系统内部,也可以是系统外部的。比如:一个健壮的系统可以容许数据输入的错误,也可以允许内部组成部件的故障。虽然在健壮性与可靠性之间有着一定的联系,但是两者是不同的测度。
课后练习题解答
-
EX2.1 下列增长函数的阶次是多少?
a.10n^2+100n+1000 n^2
b.10n^3-7 n^3
c.2n+100n3 2^n
d.n^2 ·log(n) n^2 ·log(n) -
EX2.4 请确定下面代码段的增长函数和阶次
for(int count = 0 ; count < n ; count++)
for(int count2 = 0 ; count2 < n ; count2 = count2 + 2)
{
System.out.println(count,count2);
}
}
如题,内层循环是n/2,外层循环是n,故增长函数f(n) = n^2 /2,则阶次是O(n^2)。
- EX 2.5 请确定下面代码段的增长函数和阶次
for(int count = 0 ; count < n ; count++)
for(int count2 = 1 ; count2 < n ; count2 = count2 * 2)
{
System.out.println(count,count2);
}
}
如题,内层循环次数为log(2)n,外层循环次数n,所以增长函数是nlog(2)n,而阶次只与增长函数的最高阶项有关,忽略次项与常数项,故阶次是O(nlog2n)。
结对及互评
- 本周结对学习情况
-
博客中值得学习的或问题: 课后练习题完成很认真,解析也比较详细,教材内容总结可增加些内容,侧重对知识的理解部分。
-
结对学习内容:学习第一章及第二章。
其他(感悟、思考等)
感悟
- 第一周的学习任务比较轻松,学习内容也比较简单。又到了一个新的起点,希望能够保持最开始的状态去学完这一学年,完成好这门课程。


