软件工程——大学生(误)四则运算题目生成器
Generator_Calculator
前言
司机:何卓仟
教练(安全员):何华仙
Github地址:https://github.com/hzquestion/Generator_Calculator
概述
实现一个自动生成小学生(?)四则运算题目的命令行程序。小学生暑假快乐器,生成的四则运算题不要扔,裹上鸡蛋液,粘上面包糠,下锅炸至金黄酥脆控油捞出,老人小孩都爱吃,隔壁小孩都馋哭了。
处理模式
python main.py -n [parameter] -r [parameter]
python main.py -e [parameter] -a [parameter]
说明
- 自然数:0, 1, 2, …。
- 真分数:1/2, 1/3, 2/3, 1/4, 1’1/2, …
- 运算符:+, −, ×, ÷
- 括号:(, )
- 等号:=
- 分隔符:空格(用于四则运算符和等号前后)
- 算术表达式: e = n | e1 + e2 | e1 − e2 | e1 × e2 | e1 ÷ e2 | (e),
其中e, e1和e2为表达式,n为自然数或真分数。 - 四则运算题目:e = ,其中e为算术表达式。
需求及实现情况
|
需求 |
是否实现 |
|
1. 使用 -n 参数控制生成题目的个数 |
√ |
|
2. 使用 -r 参数控制题目中数值(自然数、真分数和真分数分母)的范围 |
√ |
|
3. 生成的题目中,计算过程不会产生负数 |
√ |
|
4. 结果若不是整数,应为真分数 |
√ |
|
5. 每道题目中出现的运算符个数不超过3个 |
√ |
|
6. 程序一次运行生成的题目不能重复 |
× |
|
6.5. 生成的题目存入执行程序的当前目录下的Exercises.txt |
√ |
|
7. 当生成题目时,计算所有答案并存入执行程序的当前目录下的Answer.txt |
√ |
|
8. 程序支持10000道题目的生成 |
√ |
|
9. 对给定的题目文件和答案文件,判定答案对错并进行数量统计 |
√ |
PSP
|
PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
20 |
20 |
|
· Estimate |
· 估计这个任务需要多少时间 |
20 |
20 |
|
Development |
开发 |
1000 |
1500 |
|
· Analysis |
· 需求分析 (包括学习新技术) |
200 |
300 |
|
· Design Spec |
· 生成设计文档 |
20 |
40 |
|
· Design Review |
· 设计复审 (和同事审核设计文档) |
60 |
40 |
|
· Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
20 |
20 |
|
· Design |
· 具体设计 |
120 |
200 |
|
· Coding |
· 具体编码 |
500 |
780 |
|
· Code Review |
· 代码复审 |
40 |
60 |
|
· Test |
· 测试(自我测试,修改代码,提交修改) |
40 |
60 |
|
Reporting |
报告 |
60 |
60 |
|
· Test Report |
· 测试报告 |
30 |
30 |
|
· Size Measurement |
· 计算工作量 |
10 |
10 |
|
· Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
20 |
20 |
|
合计 |
1080 |
1580 |
设计实现过程
模块文件及其功能
|
模块 |
功能 |
|
main.py |
主函数 |
|
Generate.py |
表达式生成器 |
|
Arithmetic.py |
中缀转后缀表达式及计算器 |
|
Fetch_Proofread.py |
计算给定题目文件的答案及校对答案 |
表达式生成器
重点与难点:
- 真分数/带分数的生成
- 括号的插入位置
- 括号位置的合理性
- 查重
新建一个List来存储表达式,随机roll出运算符的个数(1~3),然后依次取 [操作数, '运算符', ……] 。其中,对操作数取 自然数/分数 的判定用 randint(0,1) 来确认。
默认情况下生成10道题目
真分数/带分数的生成,是对分数整数部分、分子、分母进行独立随机取数。
括号的插入位置,由于只有两个以上,即两个或三个运算符的情况才能插入括号,所以仅对这两种情况进行处理。
括号位置的合理性,只对 (1+2*3/4)= 此种情况进行了规避,并没有判断其他情况的合理性。
由于对数据结构尤其是二叉树的理解不深,也由于前面设计构思的时候并没有考虑好如何配合查重方面的架构,导致最后没有写出查重的算法,是此次项目的最大遗憾。
中缀转后缀表达式及计算器
通过新学习的调度场算法对生成器生成的中缀表达式转为后缀表达式,然后用逆波兰表达式求值算法进行结果的计算,此模块适用于所有符合规范的题目。
计算给定题目文件的答案和校对答案
对给定题目文件进行按行读取,然后剪切题号、等号、空格等多余内容,传入计算器进行计算并得到答案,与结果文件内容进行比对并进行记录,最后输出 Grade.txt。
代码说明
1.表达式生成器关键代码
» 表达式生成器
- 除号后不能直接取零
- 当运算符多于一个时随机确认是否插入括号
1 if randint(0, 2): # 第一个数随机取整数或分数 2 ex = [getNumber(ran)] 3 else: 4 ex = [getFraction(ran)] 5 n = randint(1, 3) # 随机取操作符的个数 6 num_op = n 7 while n > 0: 8 ex.append(getOperator()) # 随机取操作符,并加入队列 9 if randint(0, 1): 10 if ex[-1] == '÷': # 若操作符为除号,则取大于零的数 11 ex.append(getNumber(ran - 1) + 1) 12 else: 13 ex.append(getNumber(ran)) 14 else: 15 ex.append(getFraction(ran)) 16 n = n - 1 17 if num_op > 1 and randint(0, 1): # 当运算符有两个以上时,随机确认是否加入括号 18 getBrackets(ex, num_op)
» 括号插入函数
- 只有两个运算符时,左括号只有0,2两个插入位置,每种情况所对应的右括号只有一种插入情况,即-2或表尾。
- 三个运算符时的情况类似,左括号有0,2,4三个插入位置,每种情况所对应的右括号有两种插入情况。
1 if num_op == 2: 2 left_bra = randint(0, 1) * 2 3 ex.insert(left_bra, '(') 4 if left_bra: 5 ex.append(')') 6 else: 7 ex.insert(-2, ')') 8 else: 9 left_bra = randint(0, 2) * 2 10 ex.insert(left_bra, '(') 11 if left_bra == 4: 12 ex.append(')') 13 elif left_bra == 2: 14 if randint(0, 1): 15 ex.append(')') 16 else: 17 ex.insert(-2, ')') 18 elif left_bra == 0: 19 ex.insert(0 - randint(1, 2) * 2, ')')
2.中缀转后缀表达式及计算器
» 调度场算法
新建后缀表达式栈和运算符栈,为运算符赋权,遍历List
- 操作数直接入表达式栈,若遇到运算符:
- 若运算符栈空,则运算符直接入栈
- 否则取出栈顶元素,与其比较权大小
- 若栈顶元素为 '(' 或 权大于栈顶元素,入运算符栈
- 否则入表达式栈
- '(' 直接入运算符栈
- ')' 则依次取出运算符栈元素压入表达式栈,直至遇到 '('
- 操作数直接入表达式栈
1 op_weight = {'+': 1, '-': 1, '*': 2, '÷': 2} 2 suffix_exp = [] # 后缀表达式存储栈 3 op_stack = [] # 运算符栈 4 infix_exp = [str(x) for x in ex] 5 for element in infix_exp: 6 if element in ['+', '-', '*', '÷']: 7 while len(op_stack) >= 0: 8 if len(op_stack) == 0: # 若运算符栈为空,则运算符直接入栈 9 op_stack.append(element) 10 break 11 op = op_stack.pop() 12 if op == '(' or op_weight[element] > op_weight[op]: 13 op_stack.append(op) 14 op_stack.append(element) 15 break 16 else: 17 suffix_exp.append(op) 18 elif element == '(': # 若所取为左括号,则直接入运算符栈 19 op_stack.append(element) 20 elif element == ')': # 若所取为右括号,则栈顶元素依次出栈,压入表达式栈,直到遇到左括号 21 while len(op_stack) > 0: 22 op = op_stack.pop() 23 if op == '(': 24 break 25 else: 26 suffix_exp.append(op) 27 else: 28 suffix_exp.append(element) 29 30 while len(op_stack) > 0: 31 suffix_exp.append(op_stack.pop()) 32 33 return suffix_exp
» 逆波兰表达式求值算法
- 对后缀表达式(即逆波兰表达式)求值,每当取到运算符时,将栈顶元素依次弹出两个,并对其进行相应计算。
1 result_stack = [] # 结果栈 2 for element in ex: 3 if element in ['+', '-', '*', '÷']: 4 # 取到运算符,则将栈顶的两个数字弹出,并做运算,并将结果压入结果栈中 5 num2 = result_stack.pop() 6 num1 = result_stack.pop() 7 res = arithmetic(num1, num2, element) #BUG 8 if res is False: 9 return False 10 result_stack.append(res) 11 else: 12 if element.find('/') > 0: # 若取到分数,做特殊运算处理后,压入结果栈 13 int_fra = 0 14 if element.find("'") > 0: 15 li = element.split("'") 16 int_fra = int(li[0]) 17 fra = li[1] 18 else: 19 fra = element 20 li = fra.split('/') 21 nume = int_fra * int(li[1]) + int(li[0]) 22 deno = int(li[1]) 23 res = Fraction(nume, deno) 24 result_stack.append(res) 25 else: 26 result_stack.append(Fraction(int(element), 1)) # 整数直接入结果栈
3.计算给定题目文件的答案及校对答案
» 对规范题目文件进行读取并进行计算及结果对比
- 对题目文件按行读取,然后进行切片,生成计算器能读取的List
- 计算结果
- 对答案文件按行读取,切片后与计算结果逐个比对
- 将正确/错误的题数、题号输出到 Grade.txt
1 num = 1 # 题目号 2 correct_num = 0 # 正确题目数量 3 wrong_num = 0 # 错误题目数量 4 correct_list = [] # 正确题目号集合 5 wrong_list = [] # 错误题目号集合 6 try: 7 with open(file_exercise) as f1, open(file_answer) as f2, open("./Grade.txt", "w+") as Grade: 8 for exercise, answer in zip(f1.readlines(), f2.readlines()): 9 ex = exercise.split(" . ")[1].split(' = ')[0].split(' ') 10 right_answer = evaluate(suffix(ex)) 11 an = answer.split(' . ')[1].split('\n')[0] 12 if str(right_answer) == an: 13 correct_num = correct_num + 1 14 correct_list.append(num) 15 else: 16 wrong_num = wrong_num + 1 17 wrong_list.append(num) 18 num = num + 1 19 print('Correct:', correct_num, tuple(correct_list), file=Grade) 20 print('Wrong:', wrong_num, tuple(wrong_list), file=Grade) 21 except IOError: 22 print('ERROR:Please check that the path is correct and that the file exists.')
测试运行
» 命令行运行界面
» 生成10个范围为10的题目及其答案
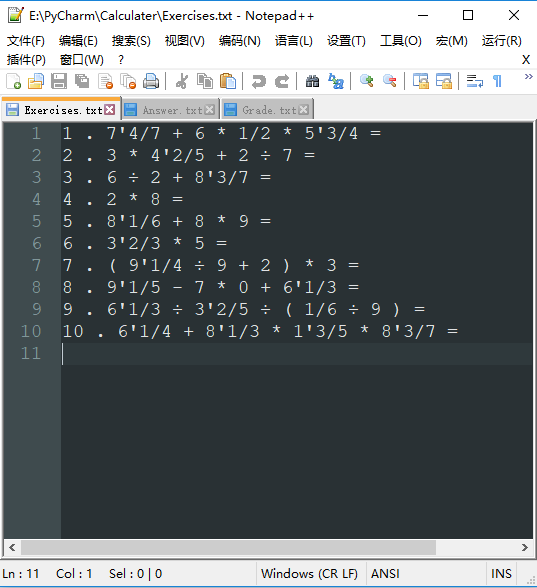
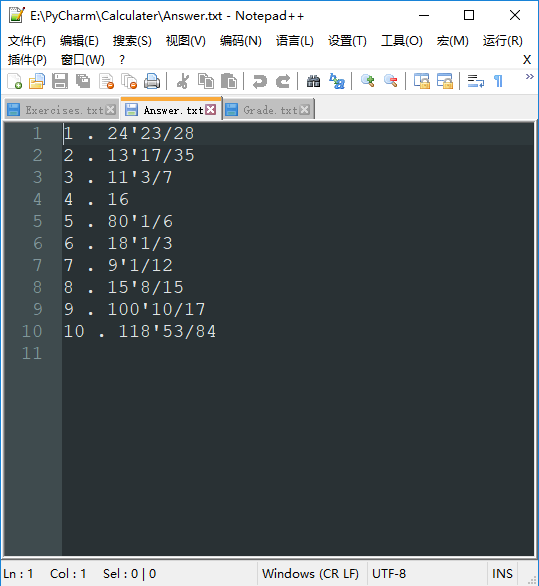
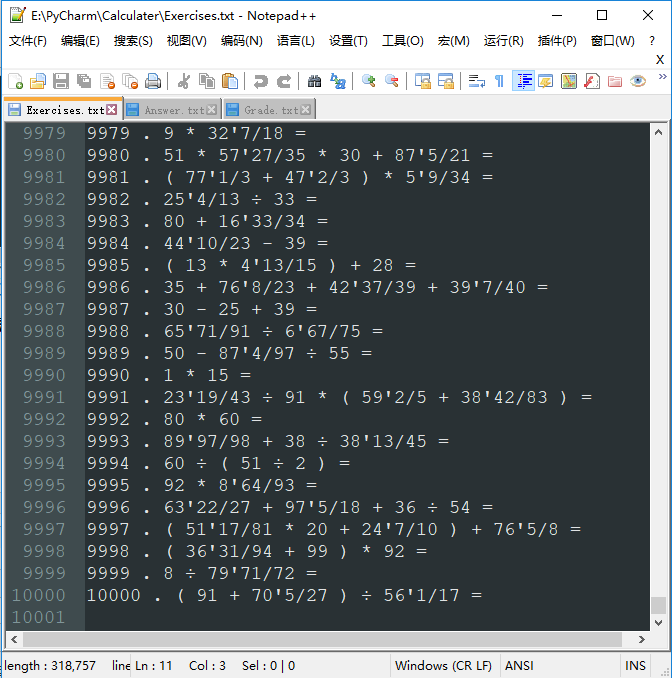
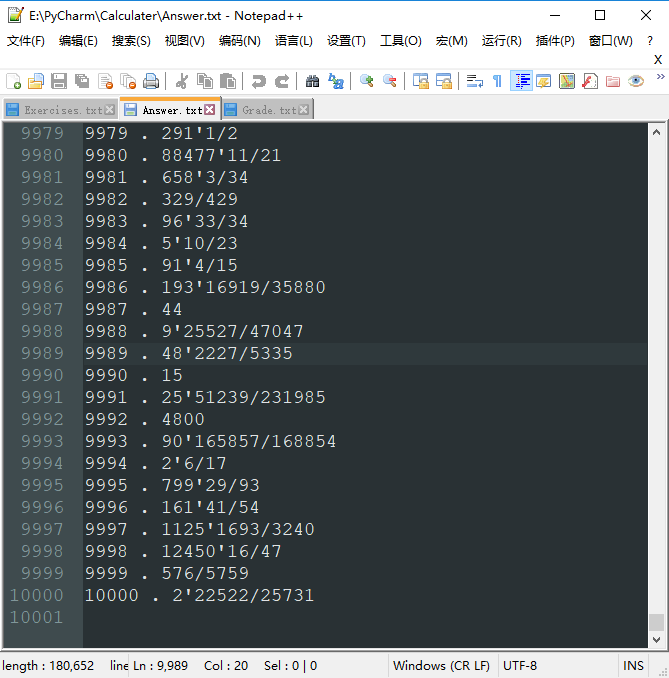
» 生成10000个范围为1000的题目及其答案的部分截图
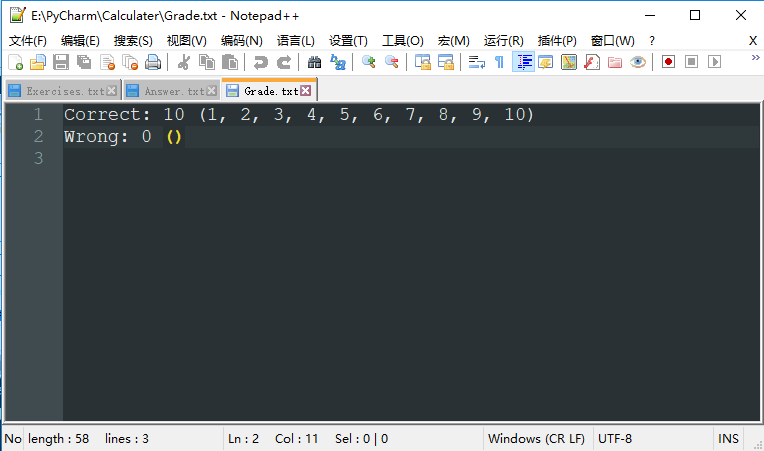
» 对规范题目文件(10题)进行校对
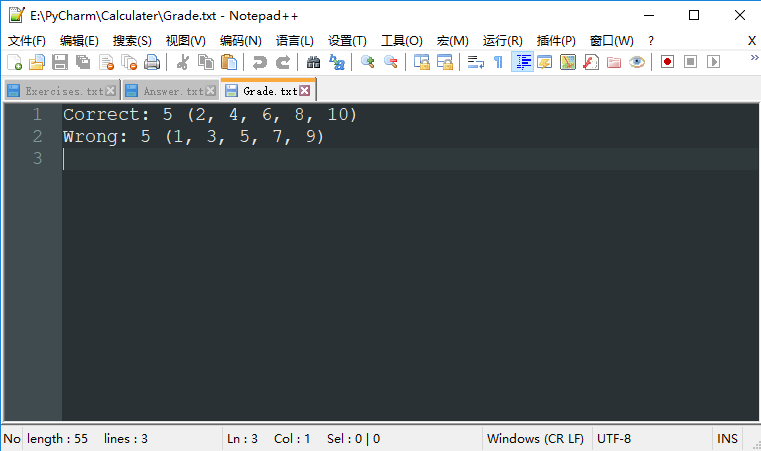
» 对规范题目文件(10题)进行校对,其中5道答案错误
项目小结
此次项目是对我们的编程能力的又一次提升,特别是对于Python的使用方面,多用多熟练。过程中也出现了许多BUG,对于调试Debug的操作也熟练了不少,新技能则是对调度场算法及逆波兰表达式求值算法的学习。然而其中未实现的查重功能是此次项目的一大遗憾,由于数据结构二叉树方面的知识不够牢固,导致查重算法迟迟未能实现,最后只能不了了之。
这次项目的另外一个方面则是对Python语言的代码运行效率有了新的认识,以及对自己设计的代码效率方面的不足有了一定的了解。由于室友之一是利用C++实现的程序,在命令行界面打印显示出题目的情况下,其代码效率能在30s内生成100w道范围为1000的题目,而我所构建的代码需要7min25s,每生成10w道题需要45s,即使是在我优化代码效率之后,每生成10w道题也需要28s,也就是说仍需要4min+才能生成100w道题目……
本次结对编程,我和何华仙一起深入分析项目的需求分析,找到实现需求的具体思路,设计具体实现的过程,我负责编码,何华仙同学在旁边指导协助。在此过程中,我们遇到了不少的问题,最后也基本上找到了解决的思路。总之,在结对编程中有很大的收获,实现了1+1 > 2 。
posted on 2018-09-28 18:56 hzquestion 阅读(273) 评论(0) 收藏 举报


 浙公网安备 33010602011771号
浙公网安备 33010602011771号