LeetCode240.二维矩阵搜索
题目#
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
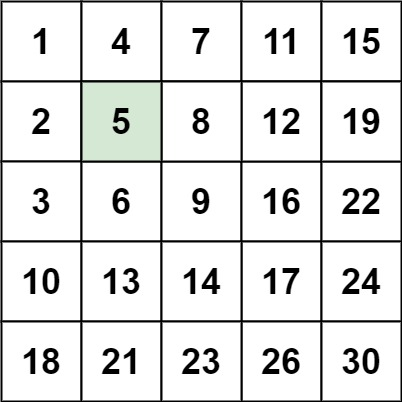
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出:false
提示:
m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-109 <= matix[i][j] <= 109
每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-109 <= target <= 109
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/search-a-2d-matrix-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题方法#
暴力破解#
时间复杂度O(mn) m*n的矩阵
空间复杂度O(1)
搜索#
时间复杂度O(m+n)每次如果没有搜索到元素返回true,行和列递增或递减,循环结束前不超过m+n次。
空间复杂度O(1)
出发点的选取:
左上角:往左或者往右都是增大,所以不能选取
右上角:往左减小往右增大,可选
左下角:往上减小往右增大,可选
右下角:往左或者网上都是减小,所以不能取
代码#
// 暴力破解
func searchMatrix(matrix [][]int, target int) bool {
row := len(matrix)
col := len(matrix[0])
for i := 0;i < row;i++{
for j := 0;j < col;j++{
if matrix[i][j] == target{
return true
}
}
}
return false
}
// 搜索 以左下角为起点
func searchMatrix2(matrix [][]int, target int) bool {
if len(matrix) == 0{
return false
}
row := len(matrix)-1
col := len(matrix[0])
index := 0
// 左下角为起点进行搜索,行列索引越界时结束
for row >= 0 && index < col{
// 当前元素等于搜索元素返回true
if matrix[row][index] == target{
return true
}
// 如果当前元素大于搜索元素,向上移动一行,否则向右移动一列
if matrix[row][index] > target {
row--
}else{
index++
}
}
return false
}




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· DeepSeek 解答了困扰我五年的技术问题
· 为什么说在企业级应用开发中,后端往往是效率杀手?
· 用 C# 插值字符串处理器写一个 sscanf
· Java 中堆内存和栈内存上的数据分布和特点
· 开发中对象命名的一点思考
· DeepSeek 解答了困扰我五年的技术问题。时代确实变了!
· PPT革命!DeepSeek+Kimi=N小时工作5分钟完成?
· What?废柴, 还在本地部署DeepSeek吗?Are you kidding?
· DeepSeek企业级部署实战指南:从服务器选型到Dify私有化落地
· 程序员转型AI:行业分析