bzoj4237 稻草人
题意不难理解吧……
一开始看到这道题的时候lrd告诉我这题要分治，还给我讲了讲分治要怎么写，好像是CDQ+树状数组来着……(好吧我已经忘了……)然而我第一眼看完题之后的思路是数据结构直接搞，本着“我就不信这个邪了”的念头，就搞出了这么一个树状数组套平衡树维护斜线的奇葩写法。
话说lrd说这题卡常，然而限时40s，我23.8s并没有什么压力，不过运行速度倒数也是感人肺腑……
(我后面就这么几个了……数据结构果然比不上CDQ……QAQ)
言归正传。
如果不用分治的话就需要按照x或者y扫描所有点，并依次处理当前点与之前的点形成的贡献和更新数据结构。
显然对于每个点，对它有贡献的点只能是在它左下角且它的右上角没有其他点的点，如图：
把这些点用线段连起来，可以得到一条斜率始终为负的斜线。如果按照y坐标从小到大处理的话，就可以以y坐标为关键字建立平衡树维护斜线。
每次查询都是前缀查询，直接在平衡树中查询即可。但是会发现一些反例，例如：
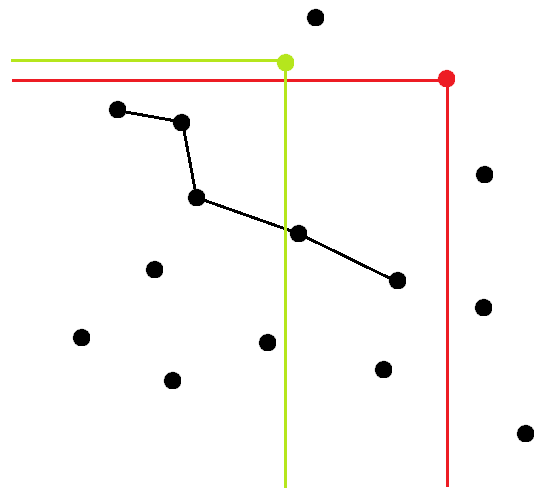
如果先插入红点的话，按照定义应该把斜线清空，只留下红点，然后查询绿点的时候就会WA。
这说明，每插入一个新点就会破坏斜线。也就是说，我们在询问的时候必须只考虑x坐标在当前点左边的点，因为按照y递增处理，只能用一个数据结构维护x。考虑到每个询问都是前缀询问，可以对x离散化后用树状数组维护x坐标，再用平衡树维护位于对应区间内的斜线即可。
查询和更新应该不难想，贴两个图跑算了。
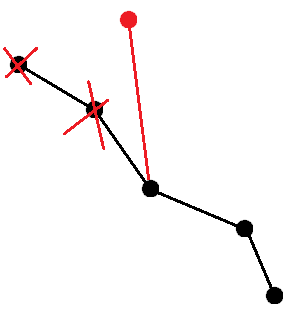
懒得写Treap了，所以用了pb_ds……如果Treap的话还要手写删除所有键值>x的数，有空再说……
1 /************************************************************** 2 Problem: 4237 3 User: hzoier 4 Language: C++ 5 Result: Accepted 6 Time:23888 ms 7 Memory:70456 kb 8 ****************************************************************/ 9 10 #include<cstdio> 11 #include<cstring> 12 #include<algorithm> 13 #include<ext/pb_ds/assoc_container.hpp> 14 #include<ext/pb_ds/tree_policy.hpp> 15 using namespace std; 16 using namespace __gnu_pbds; 17 typedef tree<int,int,less<int>,rb_tree_tag,tree_order_statistics_node_update>rbtree; 18 const int maxn=200010; 19 struct A{ 20 int x,y; 21 bool operator<(const A &a)const{return y<a.y;} 22 }a[maxn]; 23 void add(int,int); 24 int query(int); 25 int n,b[maxn]; 26 long long ans=0; 27 rbtree T[maxn]; 28 int main(){ 29 scanf("%d",&n); 30 for(int i=1;i<=n;i++){ 31 scanf("%d%d",&a[i].x,&a[i].y); 32 b[i]=a[i].x; 33 } 34 sort(b+1,b+n+1); 35 for(int i=1;i<=n;i++)a[i].x=lower_bound(b+1,b+n+1,a[i].x)-b; 36 sort(a+1,a+n+1); 37 for(int i=1;i<=n;i++){ 38 ans+=query(a[i].x); 39 add(a[i].x,a[i].y); 40 } 41 printf("%lld",ans); 42 return 0; 43 } 44 void add(int x,int y){ 45 for(int i=x;i<=n;i+=i&-i){ 46 rbtree::reverse_iterator it=T[i].rbegin(); 47 while(it!=T[i].rend()&&it->second<x){ 48 rbtree::reverse_iterator iter=++it; 49 T[i].erase(--it); 50 it=iter; 51 } 52 T[i][y]=x; 53 } 54 } 55 int query(int x){ 56 int ans=0,y=-2147483647; 57 while(x){ 58 ans+=T[x].size()-T[x].order_of_key(y); 59 if(!T[x].empty())y=max(y,T[x].rbegin()->first); 60 x&=x-1; 61 } 62 return ans; 63 }
话说这题是一边听教练放歌一边写的，结果费了两节课，这种简单题写这么久，身败名裂……
233333333
