网络吞吐量:最大流

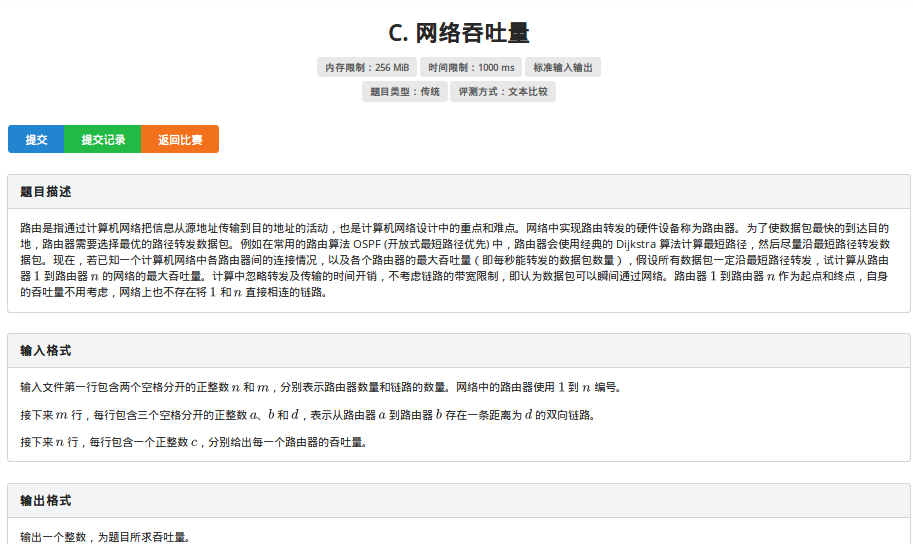
 首先要跑Dijkstra.

然后我的错误思路是记录每个点的Dis能被更新的点,接着边化点,点化边,再跑最大流即可.

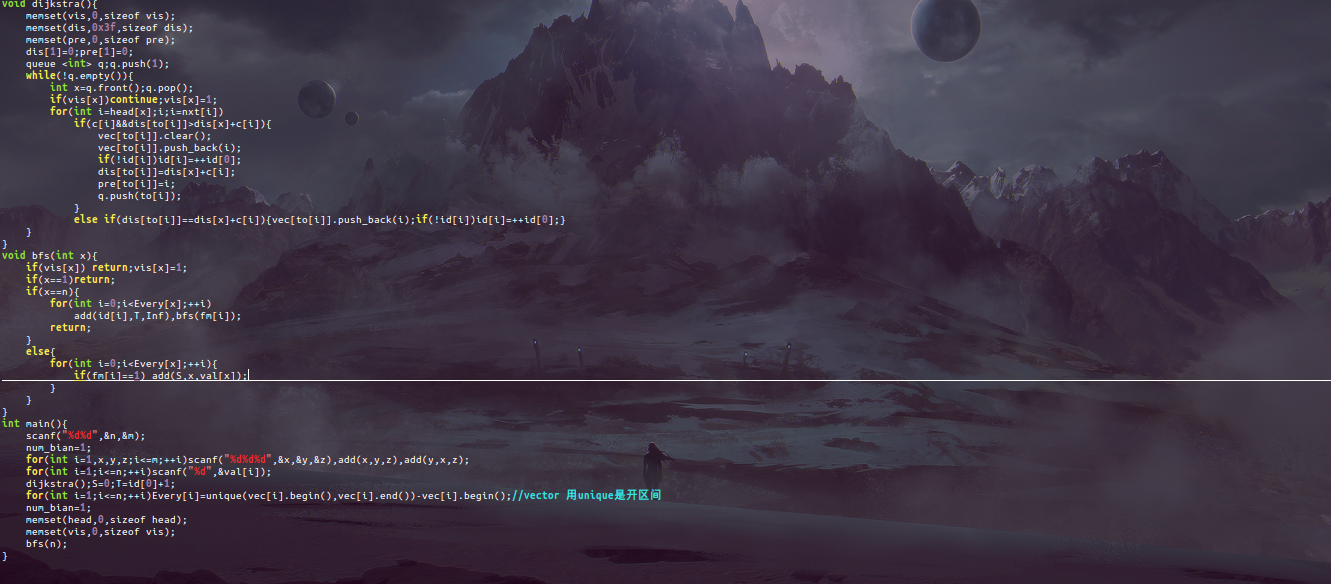
大概长这样.

但是思路就卡住了,因为我无法通过bfs找出被同一个点相连的两条边,其实能找到,只不过我判断要是边化点的话,会有200000+个点,若是每个点间连几条边,我不就死了吗.

所以我就不是人般的颓的题解.

正解:考虑每个点的贡献,也是有点相同的思想,只不过将点上的限制转化了.将最短路上的点拆成了两个点,然后其他的正常建,只不过在跑最大流时其他点的边权是Inf,只起到联通性的作用.

然后我就又想错了.我想要从S,T跑两遍Dijkstra,然后如果两种距离相加=1->n的距离,就是最短路的一部分...然后高高兴兴的码完 了...

 

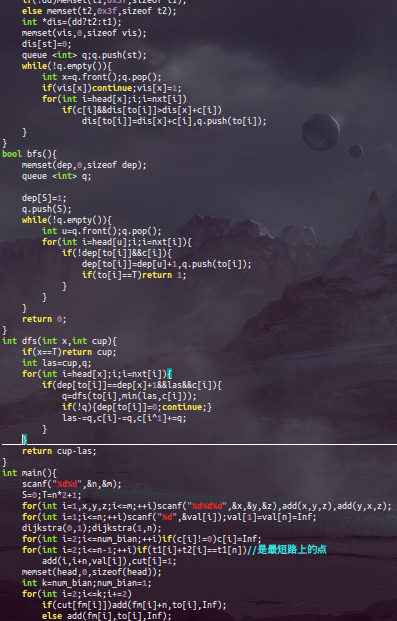
然后又发现思路不对???因为它是双向边吗??

不是的,因为这个点是最短路上的点不一定它的边们就是最短边啊!!

[打完再放代码]...

终于默默的A掉了...但是我很哭哭...

此时的思路是正解(啪

思路,也就是,跑Dijkstra,然后把最短路上的边留下来,之后愉悦的新建一个图就跑最大流就可以了.

但它是有冗余的,因为我只跑了一遍Dijkstra,用贪心策略把所有的较小边留了下来.

具体的说,我判断这个边是否是最短路上的边时是这么判断的:

那么就会出现一个问题:确实,每个点对都只会剩下一条最短边,可是,

这条边一定会用到吗?

不一定会.

因为举个例子,一条链!

然后它就会全部保留!