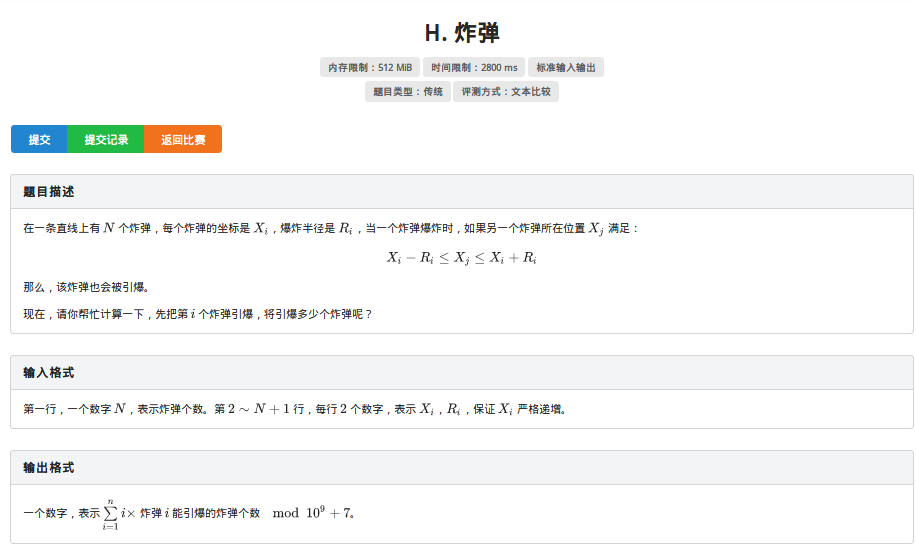
炸弹:线段树优化建边+tarjan缩点+建反边+跑拓扑

 

 这道题我做了有半个月了...终于A了...

有图为证

 一句话题解:二分LR线段树优化建边+tarjan缩点+建反边+跑拓扑统计答案

 首先我们根据题意,判断出来要炸弹可以连着炸,就是这个炸弹能炸到的可以是由它能炸到的其他炸弹来炸到.也就是说具有拓扑性.(a->b,b->c==a->c)

所以我们首先有了一个想法:建反图,tarjan缩点,跑拓扑.

为什么建反图?因为i能炸到j,所以j能炸到的i就可以炸到了,所以建反图从j->i可以实现这一点.

但是每个炸弹能炸到的是一个区间,怎么搞呢?

线段树优化建边,每次log次建边.

 1 //二分LR线段树优化建边+tarjan缩点+建反边+跑拓扑统计答案
 2 #include<bits/stdc++.h>
 3 #define N 500005
 4 #define INF 0x3f3f3f3f
 5 #define p 1000000007
 6 #define LL long long
 7 #define lch k<<1
 8 #define rch k<<1|1
 9 #define xx puts("xuefnngh");
10 using namespace std;
11 int n,num_bian,num_stack,num_dfn,num_tarjan;
12 int ls[N<<2],rs[N<<2],tree[N],mx[N<<2],mi[N<<2],head[N<<2],fm[N*20],to[N*20],nxt[N*20];
13 int dfn[N<<2],low[N<<2],sta[N<<2],in_sta[N<<2],Mi[N<<2],Mx[N<<2],bel[N<<2],in_deg[N<<2];
14 LL dis[N],R[N];
15 void add(int x,int y){if(x==y)return;/*printf("%d %d\n",x,y);*/to[++num_bian]=y;fm[num_bian]=x;nxt[num_bian]=head[x];head[x]=num_bian;}
16 void Build(int k,int l,int r){
17     ls[k]=l;rs[k]=r;mi[k]=INF;
18     if(l==r)return (void) (tree[l]=k);
19     Build(lch,l,(l+r)/2);Build(rch,(l+r)/2+1,r);
20     add(lch,k);add(rch,k);
21 }
22 void find(int k,int g,int L,int R){
23     if(ls[k]==rs[k])return (void)(mx[k]=R,mi[k]=L);
24     if(g<=rs[lch])find(lch,g,L,R);else find(rch,g,L,R);
25     mx[k]=max(mx[lch],mx[rch]);mi[k]=min(mi[lch],mi[rch]);
26 }
27 void connect(int k,int l,int r,int g){
28     if(ls[k]>=l&&rs[k]<=r) return (void) (add(k,g));
29     if(l<=rs[lch])connect(lch,l,r,g);
30     if(r>=ls[rch])connect(rch,l,r,g);
31 }
32 void tarjan(int x){
33     dfn[x]=low[x]=++num_dfn;in_sta[x]=1;sta[++num_stack]=x;
34     for(int i=head[x];i;i=nxt[i])
35         if(!dfn[to[i]])
36             tarjan(to[i]),low[x]=min(low[x],low[to[i]]);
37         else if(in_sta[to[i]])low[x]=min(low[x],dfn[to[i]]);
38     if(dfn[x]==low[x]){
39         int z;++num_tarjan;Mi[num_tarjan]=INF;
40         /*printf("huan:%d\n",num_tarjan);*/
41         do{
42             z=sta[num_stack--];
43             /*printf("%d ",z);*/
44             bel[z]=num_tarjan;
45             in_sta[z]=0;
46             Mi[num_tarjan]=min(Mi[num_tarjan],mi[z]);
47             Mx[num_tarjan]=max(Mx[num_tarjan],mx[z]);
48         }while(z!=x);
49         /*puts("");
50         printf("%d %d\n",Mi[num_tarjan],Mx[num_tarjan]);*/
51     }
52 }
53 int que[N<<2];
54 void top_sort(){
55     for(int i=1;i<=num_tarjan;++i)if(!in_deg[i])que[++que[0]]=i;
56     for(int i=1;i<=que[0];++i)
57         for(int j=head[que[i]];j;j=nxt[j]){
58             --in_deg[to[j]];
59             Mx[to[j]]=max(Mx[to[j]],Mx[que[i]]);Mi[to[j]]=min(Mi[to[j]],Mi[que[i]]);
60             if(!in_deg[to[j]])que[++que[0]]=to[j];
61         }
62 }
63 int main(){
64     scanf("%d",&n);Build(1,1,n);
65     for(int i=1;i<=n;++i)scanf("%lld%lld",&dis[i],&R[i]);
66     for(int i=1;i<=n;++i){
67         int L=lower_bound(dis+1,dis+n+1,dis[i]-R[i])-dis;
68         int RR=upper_bound(dis+1,dis+n+1,dis[i]+R[i])-dis-1;
69         /*printf("%d %d %d\n",i,L,RR);*/
70         connect(1,L,RR,tree[i]);find(1,i,L,RR);/*printf("333%d\n",tree[i]);*/
71     }
72     for(int i=1;i<=tree[n];++i)if(!dfn[i])tarjan(i);
73     /*puts("xuueue");*/
74     int num_pre=num_bian;num_bian=0;memset(head,0,sizeof head);
75     for(int i=1;i<=num_pre;++i)if(bel[fm[i]]!=bel[to[i]])add(bel[fm[i]],bel[to[i]]),in_deg[bel[to[i]]]++;
76     top_sort();
77     LL Ans=0;for(int i=1;i<=n;++i)(Ans+=(1ll*Mx[bel[tree[i]]]-Mi[bel[tree[i]]]+1)*i%p+p)%=p/*,printf("%lld\n",Ans)*/;printf("%lld",Ans);
78 }
View Code
posted @ 2019-08-02 20:45  _xuefeng  阅读(234)  评论(0)  编辑  收藏  举报