藤丸立香不明白
超几何分布
形式:\(N\)个物品中有\(M\)个次品,从所有物品中取出\(n\)个,\(X\)表示其中次品的个数
单项概率公式:\(P(X=k)=\frac{C_{M}^{k}*C_{N-M}^{m-k}}{C_{N}^{n}}\)
期望公式:\(E(X)=\frac{M}{N}*n\)
方差公式:\(D(X)=\frac{nM}{N}(1-\frac{M}{N})(1-\frac{n-1}{N-1})\)
二项分布
形式:干一件事成功的概率为\(p\),这个事干了\(n\)次(也叫\(n\)重伯努利实验)
单项概率公式:\(P(X=k)=C_{n}^{k}*p^k\)
期望公式:\(E(X)=np\)
方差公式:\(D(X)=np(1-p)\)
正态分布
定义:随机变量\(X\)服从一个数学期望为\(\mu\),方差为\(\sigma^2\)的正态分布,记为\(X\sim N(\mu,\sigma^2)\)
特殊:当\(\mu=0,\sigma=1\)时的正态分布称之为标准正态分布
图像几何意义:
-
\(\mu\)反映了图像的位置,\(\sigma\)决定了分布的幅度
-
\(X=\mu\)为函数对称轴,正态分布的期望,平均数,中位数,众数相同,均等于μ
-
\(\sigma\)越大,曲线越扁平;反之,\(\sigma\)越小,曲线越瘦高
-
\(3\sigma\)原则:
\(P(|X|<\sigma)=0.6286 \\P(|X|<2\sigma)=0.9544 \\P(|X|<3\sigma)=0.9974\)
正态分布的一些性质:若\(X\sim N(\mu_x,\sigma^2_x),Y\sim N(\mu_y,\sigma^2_y)\)是统计独立的正态随机变量
-
\(aX+b\sim N(a\mu_x+b,(a\sigma_y)^2)\)
-
\(U=X+Y\sim N(\mu_x+\mu_y,\sigma^2_x+\sigma^2_y)\)
\(V=X-Y\sim N(\mu_x-\mu_y,\sigma^2_x+\sigma^2_y)\)
\(U,V\)相互独立
-
\(\frac{X-\mu}{\sigma}\sim N(0,1)\)
原子核各种衰变及放出射线
- 原子序数大于等于\(83\)的所有元素,都能自发放出射线,但是,有的小于\(83\)的元素也具有放射性
- 天然放射现象:由贝克勒尔发现,指元素自发放出射线
\(\alpha\)衰变:\(eg\):\(^{238}_{92}U\rightarrow^{234}_{90}Th+^4_2He\)
\(\beta\)衰变:\(eg\):\(^{14}_{6}C\rightarrow^{14}_{7}N+^{0}_{-1}e\)
射线之间的比较(click to unfold)
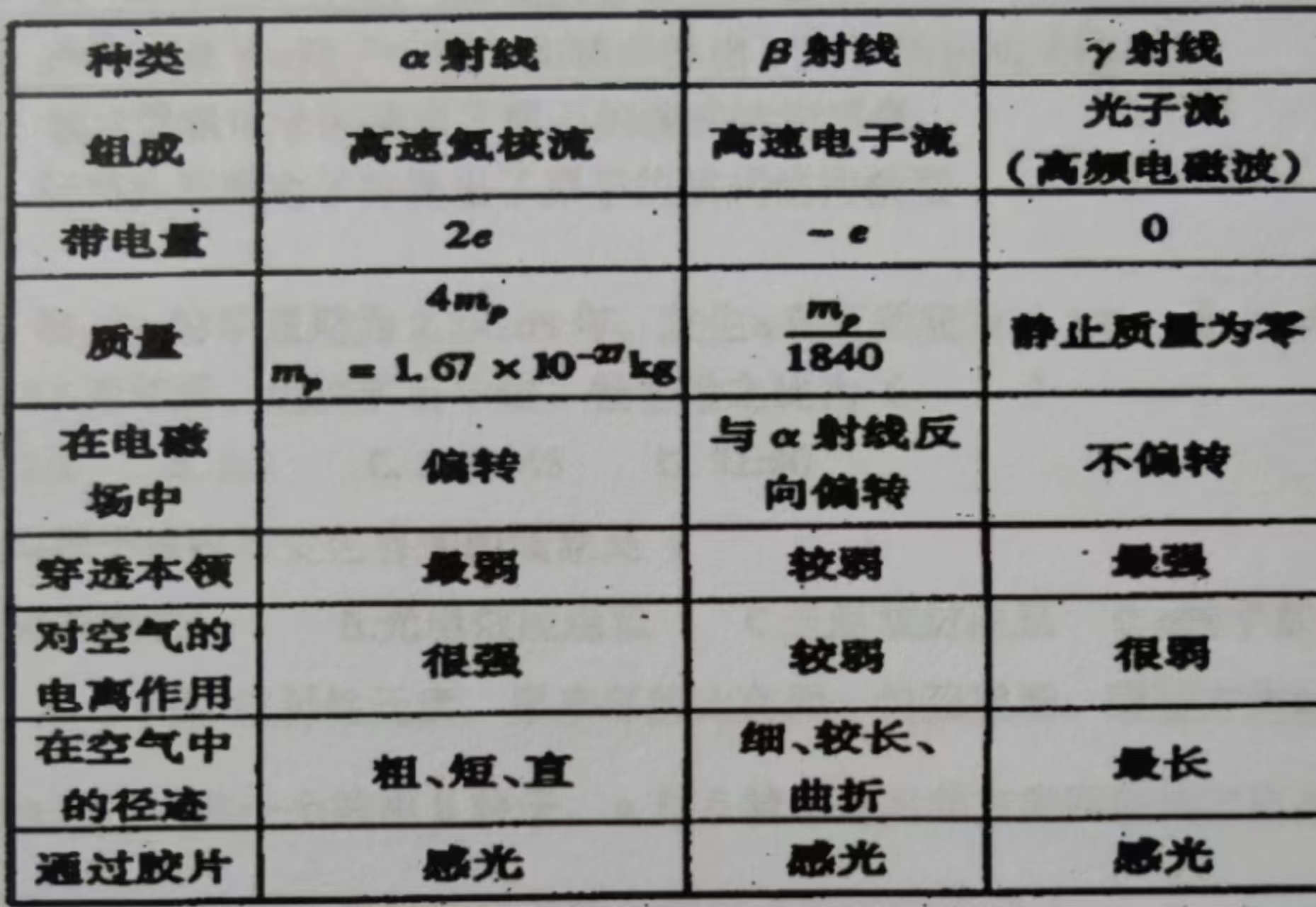
值得一提的是,\(\gamma\)射线一般不单独出现,伴随着\(\alpha,\beta\)射线而出现
研究原子核的物理学家们
- 普朗克:能量量子化\(\epsilon=hv\)(\(v\)是频率)
- 赫兹:发现光电效应
- 爱因斯坦:解释光电效应,光量子理论,提出质能方程\(E=mc^2\)
- 康普顿:康普顿效应(光是一种粒子,不仅具有能量,也具有动量\(p=\frac{h}{\lambda}\))
- \(JJ\)汤姆孙:阴极射线发现电子,提出原子核的西瓜枣糕模型,原子具有复杂的结构
- 密立根:油滴实验测定电子电荷\(e=1.602\times10^{-19}\)
- 卢瑟福:\(\alpha\)粒子散射实验,提出原子核式结构。\(\alpha\)粒子轰击氮核发现质子(\(^{4}_{2}He+^{14}_{7}N\rightarrow^{17}_{8}O+^{1}_{1}H\))
- 巴尔末:氢原子光谱及公式:\(\frac{1}{\lambda}=R(\frac{1}{2^2}-\frac{1}{n^2})(n=3,4,5,...,R为常数)\)。可以推广至紫外红外光区,叫里德伯公式\(\frac{1}{\lambda}=R(\frac{1}{n^2}-\frac{1}{m^2})\)
- 玻尔:轨道量子化,轨道半径公式\(R_n=n^2r_1\)
- 德布罗意:得到实物粒子也具有波动性,即德布罗意波,又称物质波,满足\(\lambda波长=\frac{h}{p动量},v频率=\frac{\epsilon能量}{h}\)
- 汤姆孙戴维森:电子衍射图谱,证实电子波动性
- (小居里)约里奥居里:第一次制成人工放射性同位素\(^{4}_{2}He+^{27}_{13}Al\rightarrow^{30}_{15}P+^1_0n,^{30}_{15}P\rightarrow^{30}_{14}Si+^0_{-1}e\)
- 查德威克发现中子:\(^{4}_{2}He+^{9}_{4}Be\rightarrow^{12}_{6}C+^{1}_{0}n\)

