Noip模拟89 2021.11.4
预计得分\(100+100+50+68\)
实际得分\(100+35+30+44\)
不知道说啥好。。。。非常可惜
\(TLEcoders\)的测评姬卡了大概\(20\),不可预估的\(MLE\)卡掉了\(20\)
剩下的。。。。。
\(T2\)没特判\(n=1,k=1\)挂掉了\(65\)分,只对了\(T=1\)的点。。。。
但凡\(T!=1\)的点第一个都是\(n=1,k=1\)什么鬼啊!!!
可以看出干啥事都要细心,不要因为自己已经非常接近正解就不去思考细处
否则就会有不可估量的错误让你后悔莫及。。。(别扯淡了,醒醒,喂喂)
T1 迷之阶乘
比较水,考场上应该可以直接干掉
发现他在找下降幂是否合法,那么我们直接枚举下降幂次数是\(log\)级别的
然后找到\(n^{\frac{1}{i}}\)表示可能然后下降幂次数\(\underline{i}\)合法的第一个数,一直试到\(x^{\underline{i}}\geq n\)即可
factorial
#include<bits/stdc++.h>
#define int long long
using namespace std;
namespace AE86{
auto read=[](){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
};
auto write=[](int x,char opt='\n'){
char ch[20];short len=0;if(x<0)x=~x+1,putchar('-');
do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x);
for(short i=len-1;i>=0;--i){putchar(ch[i]);}putchar(opt);
};
}using namespace AE86;
int T,n,ans;
struct answer{int x,y;}p[65];
namespace WSN{
inline short main(){
FILE *wsn=freopen("factorial.in","r",stdin);
wsn=freopen("factorial.out","w",stdout);
T=read();
while(T--){
n=read(); ans=0;
if(n==1){puts("-1");continue;}
p[++ans]=answer{n,n-1};
for(int i=2;i<64;++i){
int st=pow(1.0*n,1.0/i),res;
while(1){
res=1;
for(int j=1;j<=i;++j)
res=res*(st-j+1);
if(res>n||res<0) break;
if(res==n){
if(st-i>0)
p[++ans]=answer{st,st-i};
break;
}
++st;
}
}
write(ans);
for(int i=ans;i;--i){
write(p[i].x,' ');
write(p[i].y);
}
}
return 0;
}
}
signed main(){return WSN::main();}
T2 子集
比较水的构造,还是非正解想的时间比正解长
令\(\frac{n}{k}=m\),把输出答案看成矩阵,那么这是一个\(k\times m\)的矩阵,要求构造这个矩阵保证每一行的数加和相等。
首先特判非法解
\(\huge{n=1,k=1输出Yes!!!}\)
然后剩下的\(n=1\)输出\(No\),然后在奇数列偶数行的时候输出\(No\)
证明考虑等差数列,下面会说
先考虑\(m\)(即列数)是偶数的时候
因为\(n\)个元素构成了长度为\(1\)的等差数列,那么不难想到我们可以以每一列为单位,一条龙式的给这个数列叠起来
证明也很简单,因为这样保证了每两列的大小关系是正好相反的(即一大一小)
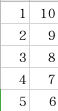
那么我们可以接着按照这种思路去想奇数列的时候
不难发现我们只构造前三列,保证前三列每一行的和是相等的,剩下的\(m-3\)行直接按照偶数的构造即可
那么为什么偶数行的时候不行呢?
我们设\(S=\frac{(1+3k)\times 3k}{2}\)表示前\(3k\)和数的和
那么如果有方案,则有\(k|S\),而\(S/k=\frac{(1+3k)\times 3}{2}\),如果\(k\)是偶数,分子一定是奇数,发现\(S\)不是\(k\)的倍数,则无解
好了,无解的都完了。。。
那么考虑奇数如何造,第一、二、三列还是\(1,2,3,4,5\),\(6,7,8,9,10\),\(11,12,13,14,15\)
我们为了保证最后一列的\(11,12,13,14,15\)放完之后和相等,就要保证前两列凑出来的数的和排完序后正好是一个长度为\(k\)的等差数列
这样之后我们就可以直接按照大小关系分配第三列的数了,即大的配小的,小的找大的(没别的意思)
所以我们现在的问题就是构造前两列,使得这两列每一行的两个数相加得到的数排完序是一个公差为一等差数列,
不难发现可以这样构造
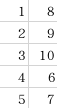
定义\(mid=(1+k)>>1\)
发现这样构造出来的行之和在\(mid\)上面全部是奇数,下面全部是偶数,\(mid\)行数最大
这样我们就解决了奇数列的问题
比题解好构造一万倍,思路也是最简单的,代码跑着也是最快的
subset
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int NN=1e6+5;
namespace AE86{
auto read=[](){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
};
auto write=[](int x,char opt='\n'){
char ch[20];short len=0;if(x<0)x=~x+1,putchar('-');
do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x);
for(short i=len-1;i>=0;--i){putchar(ch[i]);}putchar(opt);
};
}using namespace AE86;
int T,n,k,m,ans[NN];
auto id=[](int x,int y){return (x-1)*m+y;};
auto task=[](){
int tmp=0;
for(int i=1;i<=m;i++){
if(i&1) for(int j=1;j<=k;j++) ans[id(j,i)]=++tmp;
else for(int j=k;j;j--) ans[id(j,i)]=++tmp;
}
puts("Yes");
for(int i=1;i<=k;i++)
for(int j=1;j<=m;j++)
write(ans[id(i,j)],j==m?'\n':' ');
return;
};
auto solve=[](){
n=read();k=read();m=n/k;
if(n==1&&k==1){
printf("Yes\n1\n");
return;
}
if(m==1) return puts("No"),void();
if(!(m&1)) return task(),void();
if(!(k&1)) return puts("No"),void();
int tmp=0,mid=((1+k)>>1);
for(int i=1;i<=k;i++) ans[id(i,1)]=++tmp;
for(int i=mid+1;i<=k;i++) ans[id(i,2)]=++tmp;
for(int i=1;i<=mid;i++) ans[id(i,2)]=++tmp;
ans[id(mid,3)]=++tmp; int tot=0;
for(int i=1;i<=3;i++) tot+=ans[id(mid,i)];
for(int i=1;i<=k;i++)if(i!=mid)ans[id(i,3)]=tot-ans[id(i,2)]-ans[id(i,1)];
tmp=3*k;
for(int i=4;i<=m;i++){
if(i&1) for(int j=1;j<=k;j++) ans[id(j,i)]=++tmp;
else for(int j=k;j;j--) ans[id(j,i)]=++tmp;
}
puts("Yes");
for(int i=1;i<=k;i++)
for(int j=1;j<=m;j++)
write(ans[id(i,j)],j==m?'\n':' ');
return;
};
namespace WSN{
inline short main(){
FILE *wsn=freopen("subset.in","r",stdin);
wsn=freopen("subset.out","w",stdout);
T=read();
while(T--)solve();
return 0;
}
}
signed main(){return WSN::main();}
T3 混凝土粉末
考场打了一个珂朵莉树,这东西骗分真方便,不过\(MLE\)了,就比较恐怖
正解线段树加扫描线
把询问离线,维护一个时间轴一个空间轴,
空间轴用来差分,即在一个询问的\(l,r\)处分别做加减
时间轴用来线段树二分,找到最早的\(\geq y\)的\(col\)
concrete
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int NN=1e6+5;
namespace AE86{
FILE *wsn;
auto read=[](){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
};
auto write=[](int x,char opt='\n'){
char ch[20];short len=0;if(x<0)x=~x+1,putchar('-');
do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x);
for(short i=len-1;i>=0;--i){putchar(ch[i]);}putchar(opt);
};
}using namespace AE86;
int n,q,ans[NN];
struct SNOWtree{
#define lid (id<<1)
#define rid (id<<1|1)
#define mid ((l+r)>>1)
int sm[NN<<2],res,mx;
inline void pushup(int id,int l,int r){if(l==r) return;sm[id]=sm[lid]+sm[rid];}
inline void insert(int id,int l,int r,int pos,int v){
if(l==r) return sm[id]+=v,void();
if(pos<=mid) insert(lid,l,mid,pos,v);
else insert(rid,mid+1,r,pos,v);
pushup(id,l,r);
}
inline void query(int id,int l,int r,int pos){
if(res>=0||l>pos) return;
if(r<=pos){
if(l==r){
if(sm[id]>=mx) res=l;
else mx-=sm[id];
return;
}
if(mx>sm[lid]) mx-=sm[lid],query(rid,mid+1,r,pos);
else query(lid,l,mid,pos);
return;
}
query(lid,l,mid,pos);
query(rid,mid+1,r,pos);
return;
}
#undef mid
#undef lid
#undef rid
}tr;
struct node{int hi,tim;};
vector<node> add[NN],del[NN],qu[NN];
namespace WSN{
inline short main(){
wsn=freopen("concrete.in","r",stdin);
wsn=freopen("concrete.out","w",stdout);
n=read();q=read();memset(ans,-1,sizeof(ans));
int opt,l,r,h,x,y,col;
for(int i=1;i<=q;++i){
opt=read();
if(opt==1){
l=read();r=read();h=read();
add[l].push_back(node{h,i});
del[r+1].push_back(node{h,i});
}
if(opt==2){
x=read();y=read();
qu[x].push_back(node{y,i});
}
}
for(int i=1;i<=n;i++){
for(auto j:add[i]) tr.insert(1,1,q,j.tim,j.hi);
for(auto j:del[i]) tr.insert(1,1,q,j.tim,-j.hi);
for(auto j:qu[i]){
tr.res=-1; tr.mx=j.hi;
tr.query(1,1,q,j.tim);
ans[j.tim]=(tr.res==-1?0:tr.res);
}
}
for(int i=1;i<=q;i++) if(ans[i]!=-1) write(ans[i]);
return 0;
}
}
signed main(){return WSN::main();}
T4 排水系统
思路差不多和那个一样,不过就是要用两遍拓扑排序,第二遍要找哪些位置可能有出入
题解说的比较清楚,直接看就好了

water
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=998244353,NN=5e5+5;
namespace AE86{
auto read=[](){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
};
auto write=[](int x,char opt='\n'){
char ch[20];short len=0;if(x<0)x=~x+1,putchar('-');
do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x);
for(short i=len-1;i>=0;--i){putchar(ch[i]);}putchar(opt);
};
auto qmo=[](int a,int b,int ans=1){
int c=mod;for(;b;b>>=1,a=a*a%c)if(b&1)ans=ans*a%c;
return ans;
};
auto inv=[](int x){return qmo(x,mod-2);};
}using namespace AE86;
int n,m,r,k,in[NN],use[NN],out[NN],a[NN],cnt;
int pr[NN],ans[NN];
struct edge{int u,v;}p[NN];
struct SNOW{int fr,to,next;}e[NN];int head[NN],rp;
auto add=[](int x,int y){e[++rp]=SNOW{x,y,head[x]};head[x]=rp;};
queue<int> q;
auto topo=[](){
for(int i=1;i<=m;i++)q.push(i),ans[i]=1;
while(!q.empty()){
int x=q.front();q.pop();
int tmp=ans[x]*inv(out[x])%mod;
for(int i=head[x],y=e[i].to;i;i=e[i].next,y=e[i].to){
ans[y]=(ans[y]+tmp)%mod;
--in[y]; if(!in[y]) q.push(y);
}
}
};
auto retopo=[](){
memcpy(in,use,sizeof(use));
for(int i=1;i<=m;i++)q.push(i),pr[i]=1;
for(int i=1;i<=k;i++){
int fr=e[i].fr,to=e[i].to,P=a[i]*cnt%mod,tmp,res;
tmp=ans[fr]*inv(out[fr])%mod*P%mod;
res=ans[fr]*inv(out[fr]-1)%mod*P%mod;
pr[to]=(pr[to]-res+mod)%mod;
pr[fr]=(pr[fr]+out[fr]*(res-tmp+mod)%mod)%mod;
}
while(!q.empty()){
int x=q.front();q.pop(); int tmp=inv(out[x]);
for(int i=head[x],y=e[i].to;i;i=e[i].next,y=e[i].to){
--in[y]; if(!in[y]) q.push(y);
pr[y]=(pr[y]+pr[x]*tmp%mod)%mod;
}
}
};
namespace WSN{
inline short main(){
FILE *wsn=freopen("water.in","r",stdin);
wsn=freopen("water.out","w",stdout);
n=read();m=read();r=read();k=read();
for(int i=1;i<=k;++i){
int u=read(),v=read();a[i]=read();
cnt=(cnt+a[i])%mod;
add(u,v); ++in[v]; ++out[u];
}
cnt=inv(cnt);memcpy(use,in,sizeof(in));
topo(); retopo();
for(int i=n-r+1;i<=n;++i)write(pr[i],' ');puts("");
return 0;
}
}
signed main(){return WSN::main();}


