Noip模拟61 2021.9.25
T1 交通
考场上想了一个$NPC$。应该吧,是要求出图里面的所有可行的不重复欧拉路
无数种做法都无法解出,时间也都耗在这个上面的,于是就考的挺惨的
以后要是觉得当前思路不可做,就试着换一换思路,千万不能在一道题上花费太多时间
正解是一个关系的判断
每一条边选还是不选都会跟另一条边产生连锁关系,那么给他们编上号建边,用并查集判断环就行
然后每个环上选择$n$个不相邻的点,总共$2^{环数}$种方案

1 #include<bits/stdc++.h> 2 #define ll long long 3 using namespace std; 4 namespace AE86{ 5 inline int read(){ 6 int x=0,f=1;char ch=getchar(); 7 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 8 while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f; 9 }inline void write(int x,char opt='\n'){ 10 char ch[20];int len=0;if(x<0)x=~x+1,putchar('-'); 11 do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x); 12 for(int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);} 13 }using namespace AE86; 14 const int NN=2e5+5,mod=998244353; 15 inline int qmo(int a,int b,int ans=1){ 16 int c=mod; while(b){ 17 if(b&1) ans=1ll*ans*a%c; 18 b>>=1; a=1ll*a*a%c; 19 } return ans; 20 } 21 struct node{int u,v,id;}p[NN<<1]; 22 int n,in[NN<<1][2],ot[NN<<1][2],tot,fa[NN<<1]; 23 inline int getfa(int x){return fa[x]=(fa[x]==x?x:getfa(fa[x]));} 24 namespace WSN{ 25 inline short main(){ 26 freopen("a.in","r",stdin); 27 freopen("a.out","w",stdout); 28 n=read(); 29 for(int i=1;i<=n*2;i++) fa[i]=i; 30 for(int i=1;i<=n*2;i++){ 31 p[i].u=read(), p[i].v=read(); 32 if(in[p[i].v][0]) in[p[i].v][1]=i; else in[p[i].v][0]=i; 33 if(ot[p[i].u][0]) ot[p[i].u][1]=i; else ot[p[i].u][0]=i; 34 } 35 // for(int i=1;i<=n;i++) cout<<in[i][0]<<" "<<in[i][1]<<endl; 36 for(int i=1;i<=n;i++){ 37 int X=getfa(in[i][0]),Y=getfa(in[i][1]); 38 if(X==Y) ++tot; else fa[X]=Y; 39 X=getfa(ot[i][0]); Y=getfa(ot[i][1]); 40 if(X==Y) ++tot; else fa[X]=Y; 41 } 42 write(qmo(2,tot)); 43 return 0; 44 } 45 } 46 signed main(){return WSN::main();}
T2 小P的单调数列
考虑出一个结论后就非常可做了,就是关于他的价值是取平均,那么分的段越少越好
我们就只比较分成两段的情况和单调上升的情况
然后按照最大权上升子序列处理就好了,写的权值线段树,常数可能会大,可以写两个树状数组

1 #include<bits/stdc++.h> 2 #define int long long 3 using namespace std; 4 namespace AE86{ 5 inline int read(){ 6 int x=0,f=1;char ch=getchar(); 7 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 8 while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f; 9 } 10 }using namespace AE86; 11 const int NN=1e5+5; 12 int n,a[NN],dis[NN],new_n; 13 int dp1[NN],dp2[NN]; 14 struct SNOWtree{ 15 #define lid (id<<1) 16 #define rid (id<<1|1) 17 #define mid ((l+r)>>1) 18 int maxn[NN<<2]; 19 inline void insert(int id,int l,int r,int pos,int val){ 20 if(l==r){maxn[id]=max(maxn[id],val);return;} 21 if(pos<=mid) insert(lid,l,mid,pos,val); 22 else insert(rid,mid+1,r,pos,val); 23 maxn[id]=max(maxn[lid],maxn[rid]); 24 } 25 inline int query(int id,int l,int r,int ql,int qr){ 26 if(ql<=l && r<=qr) return maxn[id]; int ans=0; 27 if(ql<=mid) ans=max(ans,query(lid,l,mid,ql,qr)); 28 if(qr>mid) ans=max(ans,query(rid,mid+1,r,ql,qr)); 29 return ans; 30 } 31 }tr; 32 namespace WSN{ 33 inline short main(){ 34 freopen("b.in","r",stdin); 35 freopen("b.out","w",stdout); 36 n=read(); for(int i=1;i<=n;++i) dis[i]=a[i]=read(); 37 sort(dis+1,dis+n+1); new_n=unique(dis+1,dis+n+1)-dis-1; 38 for(int i=1;i<=n;i++) a[i]=lower_bound(dis+1,dis+new_n+1,a[i])-dis+1; 39 double maxn=0.0; 40 for(int i=1;i<=n;i++){ 41 int w1=tr.query(1,1,new_n,1,a[i]-1); 42 dp1[i]=w1+dis[a[i]-1]; 43 maxn=max(maxn,dp1[i]*1.0); 44 tr.insert(1,1,new_n,a[i],dp1[i]); 45 } 46 memset(tr.maxn,0,sizeof(tr.maxn)); 47 for(int i=n;i;i--){ 48 int w2=tr.query(1,1,new_n,1,a[i]-1); 49 dp2[i]=w2+dis[a[i]-1]; 50 tr.insert(1,1,new_n,a[i],dp2[i]); 51 } 52 // for(int i=1;i<=n;i++) cout<<dp1[i]<<" "<<dp2[i]<<endl; 53 for(int i=1;i<=n;i++){ 54 maxn=max(maxn,(dp1[i]+dp2[i]-dis[a[i]-1])/2.0); 55 } printf("%.3lf\n",maxn); 56 return 0; 57 } 58 } 59 signed main(){return WSN::main();}
T3 矩阵
神仙大模拟
当$n>=3 ,m>=3$时,考虑一个图
| + | - | |
| - | + | |
| + | - |
这样的一个小正方形按照上面的符号加起来如果不是$0$,那么他无解,
可以看出上面的是对每种操作都进行了一遍,行列斜都是一加一减
判断无解完成后考虑如何构造
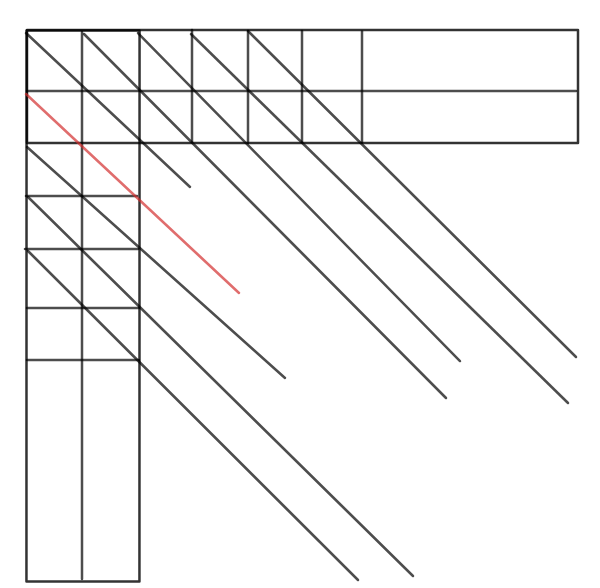
如图,每个斜线去消除,保证被削后的第二行和第一行相等,即$a[1][j+1]=a[2][j+1],j \in [1,m-1]$,这里只以列举例,
消行的让$a[i][1]=a[i][2],i \in[3,n]$,这样写是为了让红线特判,让他和$a[1][1]$相等,斜着干完列的竖着把列都干成$0$,
斜着干完行的把行干成$0$,这样就可以消完,因为不合法已经判掉,一定有解,注意要输出步数

1 #include<bits/stdc++.h> 2 #define int long long 3 using namespace std; 4 namespace AE86{ 5 inline int read(){ 6 int x=0,f=1;char ch=getchar(); 7 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 8 while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f; 9 }inline void write(int x,char opt='\n'){ 10 char ch[20];int len=0;if(x<0)x=~x+1,putchar('-'); 11 do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x); 12 for(register int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);} 13 }using namespace AE86; 14 const int NN=5005; 15 int n,m,a[NN][NN],step; 16 struct answer{ 17 int opt,x,k; 18 inline void print(){write(opt,' ');write(x,' ');write(k,' ');puts("");} 19 }ans[NN]; 20 // inline void print(){ 21 // for(int i=1;i<=n;i++){ 22 // for(int j=1;j<=m;j++){ 23 // cout<<a[i][j]<<" "; 24 // } cout<<endl; 25 // } 26 // } 27 inline void spj(){ 28 cout<<m<<endl; 29 for(int j=1;j<=m;j++) printf("2 %lld %lld\n",j,-a[1][j]); 30 } 31 namespace WSN{ 32 inline short main(){ 33 freopen("c.in","r",stdin); 34 freopen("c.out","w",stdout); 35 n=read(); m=read();for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) a[i][j]=read(); 36 if(n==1){spj(); return 0; } 37 if(n>=3 && m>=3) for(int i=1;i<=n-2;i++) for(int j=1;j<=m-2;j++) 38 if(a[i][j]-a[i][j+1]-a[i+1][j]+a[i+2][j+1]+a[i+1][j+2]-a[i+2][j+2]!=0) return puts("-1"),0; 39 for(int j=m-1;j;j--){ 40 ans[++step]=(answer){3,j-1,a[1][j+1]-a[2][j+1]}; 41 for(int jj=j,ii;jj<=m;jj++) 42 ii=jj-ans[step].x, a[ii][jj]+=ans[step].k; 43 } 44 ans[++step]=(answer){3,1-2,a[1][1]-a[2][1]}; 45 for(int jj=1,ii;jj<=m;jj++) 46 ii=jj-ans[step].x, a[ii][jj]+=ans[step].k; 47 for(int j=m;j;j--){ 48 ans[++step]=(answer){2,j,-a[1][j]}; 49 for(int i=1;i<=n;i++) a[i][j]+=ans[step].k; 50 } 51 // print(); return 0; 52 for(int i=3;i<=n;i++){ 53 ans[++step]=(answer){3,1-i,a[i][2]-a[i][1]}; 54 for(int ii=i,jj;ii<=n;ii++) 55 jj=ii+ans[step].x, a[ii][jj]+=ans[step].k; 56 } 57 for(int i=3;i<=n;i++){ 58 ans[++step]=(answer){1,i,-a[i][1]}; 59 for(int j=1;j<=m;j++) a[i][j]+=ans[step].k; 60 } 61 write(step); 62 for(int i=1;i<=step;i++) ans[i].print(); 63 return 0; 64 } 65 } 66 signed main(){return WSN::main();}
T4 花瓶
基础$dp$好想,但是时间都花在了$T1$上,没仔细打$T4$,然后就是斜率优化

比较妙的是排序,让复杂度少了一个二分凸包的$log$

1 #include<bits/stdc++.h> 2 #define int long long 3 using namespace std; 4 namespace AE86{ 5 inline int read(){ 6 int x=0,f=1;char ch=getchar(); 7 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 8 while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f; 9 }inline void write(int x,char opt='\n'){ 10 char ch[20];int len=0;if(x<0)x=~x+1,putchar('-'); 11 do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x); 12 for(register int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);} 13 }using namespace AE86; 14 const int NN=5005; 15 int n,s[NN],a[NN],id[NN]; 16 int f[NN][NN],q[NN],l,r; 17 inline bool cmp(int a,int b){ return s[a]<s[b];} 18 namespace WSN{ 19 inline short main(){ 20 freopen("d.in","r",stdin); 21 freopen("d.out","w",stdout); 22 n=read(); for(int i=1;i<=n;i++) a[i]=read(),s[i]=s[i-1]+a[i],id[i]=i; 23 sort(id,id+n+1,cmp); memset(f,-0x3f,sizeof(f)); 24 for(int i=0;i<=n;i++) f[i][0]=0; 25 for(int j=1;j<=n;j++){ 26 l=1; r=0; 27 for(int k=0;k<=n;k++) if(id[k]<j){ 28 while(l<r && (f[j][q[r]]-f[j][q[r-1]])*(s[id[k]]-s[q[r-1]])<=(f[j][id[k]]-f[j][q[r-1]])*(s[q[r]]-s[q[r-1]])) --r; 29 q[++r]=id[k]; 30 } 31 for(int i=n;~i;i--) if(id[i]>j){ 32 while(l<r && (s[id[i]]-s[j])*(s[q[l+1]]-s[q[l]])<=(f[j][q[l+1]]-f[j][q[l]])) ++l; 33 f[id[i]][j]=max(f[id[i]][j],f[j][q[l]]+(s[id[i]]-s[j])*(s[j]-s[q[l]])); 34 } 35 } 36 int maxn=0; for(int i=0;i<n;i++) maxn=max(maxn,f[n][i]); 37 write(maxn); 38 return 0; 39 } 40 } 41 signed main(){return WSN::main();}



