Noip模拟45 2021.8.21
一定别删大括号,检查是;还是,
ceil函数里面要写double,否则根本没用!!!!!!!
T1 打表
正解:打表
考场上很难真正把柿子理解着推出来
况且想要理解题意就很难,比如我就理解错了
半猜着读题思考,结果啥也不对
首先,柿子是:
$\frac{\sum_{i=1}^{2^k-1}|A_i-A_{ans}|}{2^k}$
证明用归纳法:
设$P_i$表示还有$i$个位置没有确定,期望值是剩下的数与正确输出差的平均值,也就是先假设答案的那个柿子正确
当$i=1$时,$P_1$是对的,比较好想
然后推广到$P_{i-1}$,这时的状态是比$P_i$少确定一位,这时两个$CPU$会选择同一个位置到$P_i$的状态,
那么他们的决策一定是相反的因为剩下的数与正确输出差的和是一定的
因此$P_i$也是正确的,因为选择同一位相当于将剩下的数分为了两个不相交集合

1 #include<bits/stdc++.h> 2 #define int long long 3 using namespace std; 4 namespace AE86{ 5 inline int read(){ 6 int x=0,f=1;char ch=getchar(); 7 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 8 while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f; 9 }inline void write(int x,char opt='\n'){ 10 char ch[20];int len=0;if(x<0)x=~x+1,putchar('-'); 11 do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x); 12 for(int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);} 13 }using namespace AE86; 14 15 const int NN=3e5+5,p=1e9+7; 16 int k,ans,a[NN],sum; 17 18 inline int qmo(int a,int b){ 19 int ans=1,c=p; a%=c; 20 while(b){ 21 if(b&1) ans=(ans*a)%c; 22 b>>=1; a=(a*a)%c; 23 }return ans; 24 } 25 26 namespace WSN{ 27 inline short main(){ 28 k=read();ans=read(); 29 for(int i=0;i<(1<<k);i++)a[i]=read(); 30 for(int i=0;i<(1<<k);i++) 31 (sum+=abs(a[i]-a[ans]))%=p; 32 write(sum*qmo(qmo(2,k),p-2)%p); 33 return 0; 34 } 35 } 36 signed main(){return WSN::main();}
T2 蛇
首先要明白蛇的路径一定是这样的:
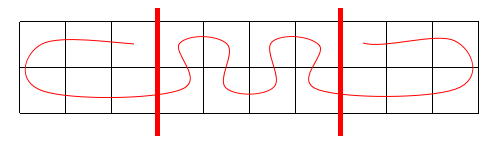
本图片粘贴自学长博客
然后分段考虑,
首先头部和尾部的两段往返可以用哈希处理出来,
然后考虑中间的扭动部分
设$dp_{i,j,k}$表示位置是$(i,j)$的时候匹配串长度为$k$的方案数,
然后进行$dp$的时候亲定一个方向,$dp$上面再加一维表示上下走还是左右走
这样的话做完一遍后把字符串反转再来一遍就行
至于考场上为了压行让代码变得好看误把大括号删掉痛失$30$分就让人很难受。。。。。。。

1 #include<bits/stdc++.h> 2 #define int long long 3 #define ULL unsigned long long 4 #define zheng 0 5 #define fannn 1 6 using namespace std; 7 namespace AE86{ 8 inline int read(){ 9 int x=0,f=1;char ch=getchar(); 10 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 11 while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f; 12 }inline void write(int x,char opt='\n'){ 13 char ch[20];int len=0;if(x<0)x=~x+1,putchar('-'); 14 do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x); 15 for(int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);} 16 }using namespace AE86; 17 18 const int NN=2005,p=1e9+7; 19 const ULL base=131; 20 int n,m,a[2][NN],b[NN],dp[2][NN][NN<<1][2],ans; 21 char ch[NN]; 22 ULL pw[NN],haa[2][NN][2],hab[NN]; 23 inline void init(){ 24 scanf("%s",ch+1);n=strlen(ch+1); 25 pw[0]=1; for(int i=1;i<=max(m,n);i++) pw[i]=pw[i-1]*base; 26 for(int i=1;i<=n;i++) a[0][i]=ch[i]-'a'+1; 27 scanf("%s",ch+1);for(int i=1;i<=n;i++) a[1][i]=ch[i]-'a'+1; 28 scanf("%s",ch+1);m=strlen(ch+1); 29 for(int i=1;i<=m;i++){ 30 b[i]=ch[i]-'a'+1; 31 hab[i]=hab[i-1]*base+(ULL)b[i]; 32 } 33 } 34 inline ULL ask(int x,int fx,int l,int r){ 35 if(fx==zheng) return haa[x][r][zheng]-haa[x][l-1][zheng]*pw[r-l+1]; 36 else return haa[x][r][fannn]-haa[x][l+1][fannn]*pw[l-r+1]; 37 } 38 inline ULL get(int l,int r){return hab[r]-hab[l-1]*pw[r-l+1];} 39 inline void calc(){ 40 for(int i=0;i<2;i++){ 41 for(int j=1;j<=n;j++) 42 haa[i][j][zheng]=haa[i][j-1][zheng]*base+(ULL)a[i][j]; 43 for(int j=n;j>=1;j--) 44 haa[i][j][fannn]=haa[i][j+1][fannn]*base+(ULL)a[i][j]; 45 } 46 for(int i=0;i<2;i++) for(int j=1;j<=n;j++){ 47 dp[i][j][1][0]=(a[i][j]==b[1]); 48 for(int k=2;k<=j;k++) 49 dp[i][j][k<<1][1]=((ask(i^1,fannn,j,j-k+1)==get(1,k))&&(ask(i,zheng,j-k+1,j)==get(k+1,k<<1))); 50 } 51 for(int k=1;k<=m;k++) for(int i=0;i<2;i++) 52 for(int j=1;j<=n;j++) if(a[i][j]==b[k]){ 53 (dp[i][j][k][0]+=dp[i][j-1][k-1][0]+dp[i][j-1][k-1][1])%=p; 54 (dp[i][j][k][1]+=dp[i^1][j][k-1][0])%=p; 55 } 56 for(int i=0;i<2;i++) for(int j=1;j<=n;j++) for(int k=0;k<=m;k++){ 57 int res=(m-k)>>1; if(((m-k)&1)==1||res==1) continue; 58 if(m==k||(j+res<=n&&ask(i,zheng,j+1,j+res)==get(k+1,k+res)&&ask(i^1,fannn,j+res,j+1)==get(m-res+1,m))) 59 (ans+=dp[i][j][k][0]+dp[i][j][k][1])%=p; 60 } 61 } 62 63 namespace WSN{ 64 inline short main(){ 65 init(); 66 calc(); 67 reverse(a[0]+1,a[0]+n+1); 68 reverse(a[1]+1,a[1]+n+1); 69 memset(dp,0,sizeof(dp)); 70 calc(); 71 if(m==1){ 72 for(int i=0;i<2;i++) for(int j=1;j<=n;j++) 73 ans-=(a[i][j]==b[1]); 74 } 75 if(m==2){ 76 for(int i=0;i<2;i++) for(int j=1;j<=n;j++) 77 ans-=(a[i][j]==b[1]&&a[i^1][j]==b[2]); 78 }write(ans); 79 return 0; 80 } 81 } 82 signed main(){return WSN::main();}
T3 购物
考场上想到正解,结果无法给出证明就遗憾收场了,因为怕爆零
可是因为$ceil$没有用$double$还是爆零了。。。。
每个数都有一个关于$k$的取值范围区间
发现加上一个数后他和原来的区间一定会产生交集
然后边维护前缀和,边判断有几段区间没有重叠,减去没有重叠的部分就是$k$的覆盖范围

1 #include<bits/stdc++.h> 2 #define int long long 3 using namespace std; 4 namespace AE86{ 5 inline int read(){ 6 int x=0,f=1;char ch=getchar(); 7 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 8 while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f; 9 }inline void write(int x,char opt='\n'){ 10 char ch[20];int len=0;if(x<0)x=~x+1,putchar('-'); 11 do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x); 12 for(int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);} 13 }using namespace AE86; 14 15 const int NN=1e5+5; 16 int n,a[NN],ans,sum,jian; 17 namespace WSN{ 18 inline short main(){ 19 n=read(); 20 for(int i=1;i<=n;i++) a[i]=read(),sum+=a[i]; 21 sort(a+1,a+n+1); 22 for(int i=1;i<=n;i++){ 23 int l=ceil(a[i]/2.0),r=a[i]; 24 int ll=ceil(a[i-1]/2.0),rr=a[i-1]; 25 if(rr<l) jian+=l-rr-1; 26 a[i]+=a[i-1]; 27 } 28 write(sum-jian); 29 return 0; 30 } 31 } 32 signed main(){return WSN::main();}
T4 ants
正解是回滚莫队。。。。丝毫没学过
然后下午就是又开始学习知识,竟是$OJ$上的一道原题
连样例都一样。。。。
每一个块内维护两个数组,$lb_i$,$rb_i$,是以值为下标的数组
表示$i$的左边的连续编号,右边的连续编号长度
在移动指针的时候维护最大的连续编号长度就行,注意重点在清除
开个栈记录更新的点和原始权值,最后只清空更改过的就行

1 #include<bits/stdc++.h> 2 #define int long long 3 using namespace std; 4 namespace AE86{ 5 inline int read(){ 6 int x=0,f=1;char ch=getchar(); 7 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 8 while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f; 9 }inline void write(int x,char opt='\n'){ 10 char ch[20];int len=0;if(x<0)x=~x+1,putchar('-'); 11 do{ch[len++]=x%10+(1<<5)+(1<<4);x/=10;}while(x); 12 for(int i=len-1;i>=0;--i)putchar(ch[i]);putchar(opt);} 13 }using namespace AE86; 14 15 const int NN=1e5+5; 16 int n,m,a[NN],top,sq; 17 int ls[NN],rs[NN],res[NN]; 18 19 struct SNOW{int l,r,k,id;}q[NN]; 20 struct stac{int pos,val;}stk[NN]; 21 22 inline bool cmp(SNOW a,SNOW b){return a.k==b.k?a.r<b.r:a.l<b.l;} 23 24 namespace WSN{ 25 inline short main(){ 26 // freopen("1.in","r",stdin); 27 n=read();m=read();sq=sqrt(n); 28 for(int i=1;i<=n;i++) a[i]=read(); 29 for(int i=1;i<=m;i++){ 30 int l=read(),r=read(); 31 q[i]=(SNOW){l,r,(l-1)/sq+1,i}; 32 } 33 sort(q+1,q+m+1,cmp); 34 35 int l=1,r=0,ans=0; 36 for(int i=1;i<=m;i++){ 37 int ql=q[i].l,qr=q[i].r; 38 if(q[i].k!=q[i-1].k){ 39 memset(ls,0,sizeof(ls)); 40 memset(rs,0,sizeof(rs)); 41 l=r=q[i].k*sq; ans=0; 42 } 43 while(r<qr){ 44 ++r; 45 ls[a[r]]=ls[a[r]-1]+1; 46 rs[a[r]]=rs[a[r]+1]+1; 47 int len=ls[a[r]]+rs[a[r]]-1; 48 int L=a[r]-ls[a[r]]+1; 49 int R=a[r]+rs[a[r]]-1; 50 ls[R]=rs[L]=len; 51 ans=max(ans,len); 52 } 53 int tmp=ans; top=0; 54 for(int j=ql;j<=min(qr,l);j++){ 55 ls[a[j]]=ls[a[j]-1]+1; 56 rs[a[j]]=rs[a[j]+1]+1; 57 int len=ls[a[j]]+rs[a[j]]-1; 58 int L=a[j]-ls[a[j]]+1; 59 int R=a[j]+rs[a[j]]-1; 60 stk[++top]=(stac){R,ls[R]}; 61 stk[++top]=(stac){L,rs[L]}; 62 ls[R]=rs[L]=len; 63 tmp=max(tmp,len); 64 } 65 for(int j=top;j;j--) 66 if(j&1) ls[stk[j].pos]=stk[j].val; 67 else rs[stk[j].pos]=stk[j].val; 68 for(int j=ql;j<=min(qr,l);j++) 69 ls[a[j]]=rs[a[j]]=0; 70 res[q[i].id]=tmp; 71 } 72 for(int i=1;i<=m;i++) write(res[i]); 73 return 0; 74 } 75 } 76 signed main(){return WSN::main();}
麻辣烫真香!!!!!!!!



