Noip模拟41 2021.8.16
T1 你相信引力吗
对于区间的大小关系问题,往往使用单调栈来解决
这道题的优弧和劣弧很烦,考虑将其等价的转化
由于所有的合法情况绕过的弧都不会经过最高的冰锥,
又因为环可以任意亲定起点,这样可以直接把最大的点当作起点
那么我们所找的合法的答案就应该是:
在起点的右侧的冰锥配对,以及可以绕过来和起点配对的组合
这样就可以用单调栈维护,去重再开一个数组记录栈顶元素个数就行

1 #include<bits/stdc++.h> 2 #define LL long long 3 using namespace std; 4 inline int AE86(){ 5 int x=0,f=1; char ch=getchar(); 6 while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); } 7 while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar();} 8 return x*f; 9 } 10 const int NN=1e7+5; 11 int n,a[NN],top,stk[NN],maxn,bin[NN]; 12 LL ans; 13 namespace WSN{ 14 inline short main(){ 15 n=AE86(); 16 for(register int i=1;i<=n;++i) a[i+n]=a[i]=AE86(); 17 for(register int i=1;i<=n;++i) if(a[maxn]<a[i]) maxn=i; 18 for(register int i=maxn;i<=maxn+n-1;++i){ 19 while(top&&stk[top]<a[i]) ++ans,--top; 20 stk[top]>a[i] ? (++ans):(ans+=bin[top]+(a[i]!=a[maxn])); 21 stk[++top]=a[i]; 22 bin[top]=(a[i]==stk[top-1]?(bin[top-1]+1):(1)); 23 } 24 while(top>2){ 25 if(stk[top]==stk[2]) break; 26 ++ans,--top; 27 } 28 printf("%lld\n",ans); 29 return 0; 30 } 31 } 32 signed main(){return WSN::main();}
T2 marshland
一眼网络流,可是忘记了$dinic$,考场上比较傻眼
不过没事,这不是最大流,费用流我还没学过,所以就没什么抱怨的
这种题比较套路的做法是一个偶点旁边有上下左右四个奇点,在奇数行的和偶点的入点连边
偶数行的和偶点的出点连边,最后大概长这样:
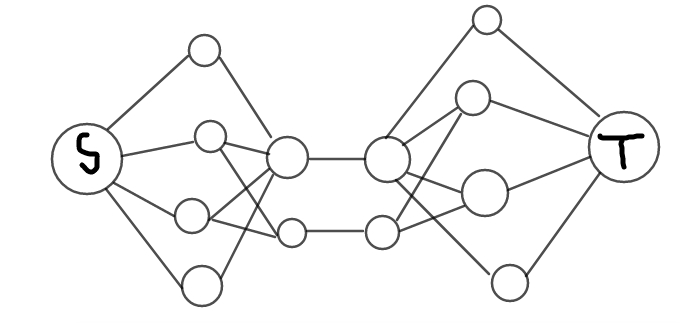
然后跑费用流$EK$板子,稍微魔改一下,跑的过程中记录答案就行

1 #include<bits/stdc++.h> 2 using namespace std; 3 inline int AE86(){ 4 int x=0,f=1; char ch=getchar(); 5 while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); } 6 while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar();} 7 return x*f; 8 } 9 const int NN=1100,inf=2e9,MM=1e6+5; 10 int n,m,k,S,T,g[NN][NN]; 11 int maxflow,mincost,ans,sum; 12 int pre[MM],incf[MM],dis[MM]; 13 bool vis[MM],jin[NN][NN]; 14 struct SNOW{int to,next,flow,val;}; SNOW e[MM<<1]; int head[MM],rp=1; 15 inline void add(int x,int y,int w,int c){ 16 e[++rp]=(SNOW){y,head[x],w,c}; head[x]=rp; 17 e[++rp]=(SNOW){x,head[y],0,-c};head[y]=rp; 18 } 19 queue<int> q; 20 inline bool spfa(){ 21 memset(dis,-0x3f,sizeof(dis)); 22 memset(vis,0,sizeof(vis)); 23 dis[S]=0; vis[S]=1; q.push(S); incf[S]=1<<30; 24 while(!q.empty()){ 25 int x=q.front(); q.pop(); vis[x]=0; 26 for(register int i=head[x],y;i;i=e[i].next){ 27 if(!e[i].flow) continue; 28 if(dis[y=e[i].to]<dis[x]+e[i].val){ 29 dis[y]=dis[x]+e[i].val; pre[y]=i; 30 incf[y]=min(incf[x],e[i].flow); 31 if(!vis[y]) vis[y]=1,q.push(y); 32 } 33 } 34 } 35 if(dis[T]<0) return 0; 36 return 1; 37 } 38 inline void EK(){ 39 while(spfa()){ 40 int x=T; 41 if(maxflow+incf[T]>m) break; 42 maxflow+=incf[T]; 43 mincost=max(mincost,mincost+dis[T]*incf[T]); 44 while(x!=S){ 45 int i=pre[x]; 46 e[i].flow-=incf[T]; 47 e[i^1].flow+=incf[T]; 48 x=e[i^1].to; 49 } 50 ans=min(ans,sum-mincost); 51 } 52 } 53 inline int id(int x,int y,int opt){return n*(x-1)+y+opt*n*n;} 54 namespace WSN{ 55 inline short main(){ 56 n=AE86(); m=AE86(); k=AE86(); S=n*n*2+1; T=S+1; 57 for(register int i=1;i<=n;++i) for(register int j=1;j<=n;++j){ 58 g[i][j]=AE86(); sum+=g[i][j]; 59 if(!g[i][j]) 60 if(i&1) add(S,id(i,j,0),1,0); 61 else add(id(i,j,0),T,1,0); 62 } 63 for(register int i=1;i<=k;++i) jin[AE86()][AE86()]=1; 64 for(register int i=1;i<=n;++i) for(register int j=1;j<=n;++j) if(g[i][j]){ 65 if(i&1){ 66 if(j-1>0&&!jin[i][j-1]) add(id(i,j-1,0),id(i,j,0),1,0); 67 if(j+1<=n&&!jin[i][j+1]) add(id(i,j+1,0),id(i,j,0),1,0); 68 if(i+1<=n&&!jin[i+1][j]) add(id(i,j,1),id(i+1,j,0),1,0); 69 if(i-1>0&&!jin[i-1][j]) add(id(i,j,1),id(i-1,j,0),1,0); 70 }else{ 71 if(i+1<=n&&!jin[i+1][j]) add(id(i+1,j,0),id(i,j,0),1,0); 72 if(i-1>0&&!jin[i-1][j]) add(id(i-1,j,0),id(i,j,0),1,0); 73 if(j-1>0&&!jin[i][j-1]) add(id(i,j,1),id(i,j-1,0),1,0); 74 if(j+1<=n&&!jin[i][j+1]) add(id(i,j,1),id(i,j+1,0),1,0); 75 }add(id(i,j,0),id(i,j,1),1,g[i][j]); 76 } 77 ans=sum; EK(); 78 printf("%d\n",ans); 79 return 0; 80 } 81 } 82 signed main(){return WSN::main();}
T3 party?
考场上做完了预处理的工作,然后就傻眼了,因为T2看出网络流
这题就没有往那里想,网络流可以拿到暴力分其实
先用$bitset$预处理出每一条路径有多少中可能选择的特产,线段树+树剖比较显然
然后就是考虑如何满足题意找到最大合法情况
我们建一个二分图,左部点是人,右部点是特产,每个人分裂成答案个
这样的话,让二分图实现完美匹配即可。
问题转化成要找到一个满足可以二分图完美匹配的最大的$k$
然后引入一个霍尔定理(雾)
一个二分图(G)存在完美匹配, 当且仅当(X)中的任意(k)个点都至少与(Y)中的(k)个点邻接.
左部$c*k$个点只有$c$种邻接关系不同的点,所以$2^c$枚举子集,用$bitset$取并找邻接点个数
则最大的$k$即为邻接点个数和子集个数比值最小值

1 #include<bits/stdc++.h> 2 #define bs bitset<1005> 3 #define lid (id<<1) 4 #define rid (id<<1|1) 5 using namespace std; 6 inline int AE86(){ 7 int x=0,f=1; char ch=getchar(); 8 while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); } 9 while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar();} 10 return x*f; 11 } 12 inline int min(int a,int b){return a<b?a:b;} 13 inline void swap(int &a,int &b){a^=b^=a^=b;} 14 const int NN=3e5+1; 15 bs b[NN]; 16 int n,m,q,a[NN],ci[NN],num,ans,c,lca; 17 int dfn[NN],rk[NN],son[NN],fa[NN],siz[NN],dep[NN],top[NN],cnt; 18 struct SNOW{int to,next;};SNOW e[NN<<1]; int head[NN],rp; 19 inline void add(int x,int y){ 20 e[++rp]=(SNOW){y,head[x]};head[x]=rp; 21 e[++rp]=(SNOW){x,head[y]};head[y]=rp; 22 } 23 struct SNOWtree{ 24 int ll[NN<<2],rr[NN<<2]; bs te[NN<<2]; 25 inline void pushup(int id){ 26 if(ll[id]==rr[id]) return; 27 te[id]=te[lid]|te[rid]; 28 } 29 inline void build(int id,int l,int r){ 30 ll[id]=l;rr[id]=r; 31 if(l==r){te[id][a[rk[l]]]=1;return;} 32 int mid=l+r>>1; 33 build(lid,l,mid); build(rid,mid+1,r); 34 pushup(id); 35 } 36 inline bs query(int id,int l,int r){ 37 if(l<=ll[id]&&rr[id]<=r) return te[id]; 38 int mid=ll[id]+rr[id]>>1; bs ans; 39 if(l<=mid) ans|=query(lid,l,r); 40 if(r>mid) ans|=query(rid,l,r); 41 return ans; 42 } 43 }tr; 44 inline void dfs1(int f,int x){ 45 dep[x]=dep[f]+1; siz[x]=1; 46 for(register int i=head[x],y;i;i=e[i].next) if((y=e[i].to)!=f){ 47 dfs1(x,y); siz[x]+=siz[y]; 48 if(siz[son[x]]<siz[y]) son[x]=y; 49 } 50 } 51 inline void dfs2(int x,int t){ 52 top[x]=t; dfn[x]=++cnt; rk[cnt]=x; 53 if(x!=t) b[x]=b[fa[x]]; b[x].set(a[x]); 54 if(son[x]) dfs2(son[x],t); 55 for(register int i=head[x],y;i;i=e[i].next) if((y=e[i].to)!=fa[x]&&y!=son[x]) dfs2(y,y); 56 } 57 inline int LCA(int x,int y){ 58 while(top[x]!=top[y]){ 59 if(dep[top[x]]<dep[top[y]]) swap(x,y); 60 x=fa[top[x]]; 61 }if(dfn[x]>dfn[y]) swap(x,y); 62 return x; 63 } 64 inline bs query(int x,int y){ 65 bs ans; 66 while(top[x]!=top[y]){ 67 if(dep[top[x]]<dep[top[y]]) swap(x,y); 68 ans|=b[x]; 69 x=fa[top[x]]; 70 }if(dfn[x]>dfn[y]) swap(x,y); 71 ans|=tr.query(1,dfn[x],dfn[y]); 72 return ans; 73 } 74 namespace WSN{ 75 inline short main(){ 76 n=AE86();m=AE86();q=AE86(); if(!q) return 0; 77 for(register int i=2;i<=n;++i) fa[i]=AE86(),add(i,fa[i]); 78 for(register int i=1;i<=n;++i) a[i]=AE86(); 79 dfs1(0,1);dfs2(1,1);tr.build(1,1,n); 80 while(q--){ 81 c=AE86(); bs tmp[6]; ci[1]=AE86(); ci[2]=AE86(); 82 ans=0x3fffffff; lca=LCA(ci[1],ci[2]); 83 for(register int i=3;i<=c;++i) ci[i]=AE86(),lca=LCA(lca,ci[i]); 84 for(register int i=1;i<=c;++i) tmp[i]=query(ci[i],lca); 85 for(register int s=1;s<(1<<c);++s){ 86 bs cc;num=0; 87 for(register int i=0;i<c;++i) if((1<<i)&s) ++num,cc|=tmp[i+1]; 88 ans=min(ans,(int)cc.count()/num); 89 }printf("%d\n",ans*c); 90 } 91 return 0; 92 } 93 } 94 signed main(){return WSN::main();}
T4 半夜
沽沽沽


