差分[差分数组 & 树状差分]

差分[差分数组 & 树状差分]

1. 差分数组

• 差分数组的定义：记录当前位置的数与上一位置的数的差值.

原数组 ai	9	4	7	5	9
差分数组 bi	9	-5	3	-2	4
差分数组的前缀和	9	4	7	5	9

显然通过求前缀和可以做到单点查询

他高效的地方在于区间修改,比如我们对区间[2,4]每个元素加上5，我们只需在差分数组：b2+=5,b5−=5，然后求前缀和即可

原数组 ai	9	4	7	5	9
差分数组 bi	9	0	3	-2	-1
差分数组的前缀和	9	9	12	10	9

[1,2]仍不变, [2,4]的前缀和都加了5, 4以后的话+5,-5相抵消, 还是不变的

因此差分数组能够高效的解决区间修改单点查询的问题。

2. 树状差分

树的以下两个性质：

1. 任意两个节点之间有且只有一条路径。
2. 根节点确定时，一个节点只有一个父亲节点。

如果假设我们要考虑的是从u到v的路径，u与v的lca是a，,我们将路径拆分成 u->a和a->v

如果题目要求对树上的一段路径进行操作，并询问某个点或某条边被经过的次数，树上差分就可以派上用场了。

点差分

设原数组为a，差分数组为d。假如给d[i]+1，其实就相当于给a[i]~a[n]每个元素+1

如果给树上的一个节点x的d[x] +1, 相当于a[root]~a[x]链上的每个节点都+1

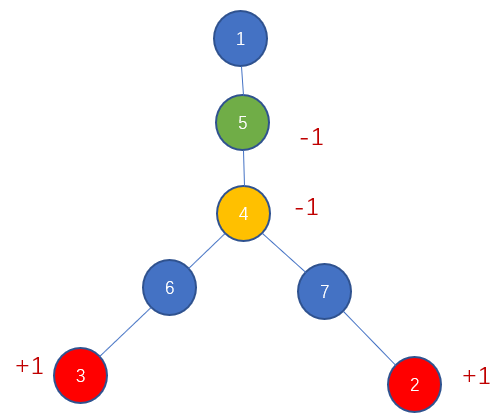
假设a=lca(x,y)。 把链x~y分成两个链，x~a和a~y。即d[x]+1,d[y]+1。

但这样链a~root增加了2，我们让d[a]-1，此时fa[a]~root变成了-1，需要d[fa[a]]-1完美解决。

例题：松鼠的新家(luogu p3258)

Description

• 松鼠的新家是一棵树，前几天刚刚装修了新家，新家有n个房间，并且有 n-1 根树枝连接，每个房间都可以相互到达，且俩个房间之间的路线都是唯一的。天哪，他居然真的住在“树”上。
• 松鼠想邀请小熊前来参观，并且还指定一份参观指南，他希望小熊能够按照他的指南顺序，先去 a1a1，再去 a2a2，……，最后到 anan，去参观新家。可是这样会导致重复走很多房间，懒惰的维尼不停地推辞。可是松鼠告诉他，每走到一个房间，他就可以从房间拿一块糖果吃。
• 小熊是个馋家伙，立马就答应了。现在松鼠希望知道为了保证维尼有糖果吃，他需要在每一个房间各放至少多少个糖果。
• 因为松鼠参观指南上的最后一个房间 anan 是餐厅，餐厅里他准备了丰盛的大餐，所以当维尼在参观的最后到达餐厅时就不需要再拿糖果吃了。

Input

• 第一行一个正整数 n，表示房间个数
• 第二行 n个正整数，依次描述 a1,a2,⋯,ana1,a2,⋯,an。
• 接下来 n-1 行，每行两个正整数 x,y，表示标号 x 和 y的两个房间之间有树枝相连。

Output

• 一共 n 行，第 i 行输出标号为 i 的房间至少需要放多少个糖果，才能让小熊有糖果吃。

Input

5
1 4 5 3 2
1 2
2 4
2 3
4 5

output

1
2
1
2
1    

#include <bits/stdc++.h>
using namespace std;
const int maxn=3e5+5;
struct edge{ int to,next; }e[2*maxn];
int n, len, a[maxn], head[maxn], dep[maxn], f[maxn][21], sum[maxn];
void Insert(int u, int v){ e[++len].to=v;e[len].next=head[u];head[u]=len; }
void dfs(int u, int fa){//dfs预处理祖先, 不用多说吧
    dep[u] = dep[fa]+1; f[u][0] = fa;
    for(int i=1; (1<<i)<=dep[u]; i++) f[u][i] = f[f[u][i-1]][i-1];
    for(int i=head[u]; i; i=e[i].next){
        int v = e[i].to;
        if(v != fa) dfs(v, u);
    }
}
int lca(int u, int v){//获取lca
    if(dep[u] < dep[v]) swap(u, v);
    int len = dep[u]-dep[v], k = 0;
    while(len){
        if(len & 1)u=f[u][k];
        ++k; len>>=1;
    }    
    if(u==v) return u;
    for(int i=20; i>=0; i--) if(f[u][i] != f[v][i]) u = f[u][i], v = f[v][i];            
    return f[u][0];
}
void search(int u){//求每个节点的差分和
    for(int i=head[u]; i; i=e[i].next){
        int v = e[i].to;
        if(v == f[u][0]) continue;
        search(v);
        sum[u] += sum[v];
    }
}
int main(){
    scanf("%d", &n);
    for(int i=1; i<=n; i++) scanf("%d",&a[i]);
    for(int i=1; i<=n-1; i++){
        int u, v; scanf("%d%d", &u, &v);
        Insert(u, v); Insert(v, u);
    }
    dfs(1,0);
    for(int i=1; i<=n-1; i++){
        int x=a[i], y=a[i+1], LCA=lca(x,y);        
        sum[x]++;
        sum[y]++;
        sum[LCA]--;
        sum[f[LCA][0]]--;
    }
    search(1);
    for(int i=2; i<=n; i++) sum[a[i]]--;//2-n的点都多算了一次
    for(int i=1; i<=n; i++) printf("%d\n",sum[i]);
    return 0;
}

边差分

用cf[i]代表从i到i的父亲这一条路径经过的次数。令a=lca(u,v) 因为关于边的差分，a表示a到其父亲的那条边，不在u~v路径中，所以cf[u]++,cf[v]++,cf[a]−=2。

• 例题：luogu P2680 运输计划
• 题意：一棵树上有m条道路，可以使任意一条道路的权值变为0，怎样使长度最长的道路长度最小。

思路 最小的长度, 肯定在 0 - maxl(最长的那条道路) 之间, 我们可以用二分在 0-maxl枚举, 每次枚举统计长度超过mid的路径的条数cnt, 找到一条被经过了cnt次的边(这条边可以影响所有长度超过mid的路径), 把符合条件的边中最长的那一条归零, 如果cnt条路径中最长的减去这条边权<=mid, 则当前的mid合法.

#include <bits/stdc++.h>
using namespace std;
const int maxn=3e5+5;
int f[maxn][22],head[maxn],edge[maxn],dep[maxn],dis[maxn];
int st[maxn],ed[maxn],c[maxn],lca[maxn],len[maxn];
int n,m,lene,maxl,ans,cnt,max_edge;
struct Edge{int to,w,next;}e[maxn<<1];
void Insert(int x,int y,int z){e[++lene].to=y; e[lene].w=z; e[lene].next=head[x]; head[x]=lene;}
void dfs(int u){//dfs预处理祖先
    dep[u] = dep[f[u][0]] + 1;
    for(int i=1; (1<<i)<=dep[u]; i++) f[u][i]=f[f[u][i-1]][i-1];
    for(int i=head[u]; i; i=e[i].next){
        int v=e[i].to;
        if(v==f[u][0])continue;
        f[v][0]=u;
        edge[v]=e[i].w;//edge[v]记录v到父节点u的边长
        dis[v]=dis[u]+e[i].w;//求解v到根节点的距离
        dfs(v);
    }
}
int Lca(int u,int v){
    if(dep[u] < dep[v]) swap(u, v);
    int len = dep[u]-dep[v], k = 0;
    while(len){
        if(len & 1) u = f[u][k];
        ++k; len >>= 1;
    }
    if(u==v) return u;
    for(int i=20; i>=0; i--) if(f[u][i] != f[v][i]) u = f[u][i], v = f[v][i];
    return f[u][0];
}
int getdis(int i){ return dis[st[i]] + dis[ed[i]] - 2*dis[lca[i]]; } //求第i条路径长度
int dfs2(int u){
    int tot = c[u];//计算u到其父亲这条边访问次数
    for(int i=head[u]; i; i=e[i].next){
        int v = e[i].to;
        if(v==f[u][0])continue;
        tot += dfs2(v);
    }
    if(tot==cnt) max_edge = max(max_edge, edge[u]);
    return tot;
}
bool check(int mid){
    cnt=0, max_edge=0;//cnt记录超过mid的路径数，max_edge记录要删掉的边
    for(int i=1; i<=n; i++) c[i] = 0;//差分数组清零 
    for(int i=1; i<=m; i++)
        if(len[i] > mid)//超出mid的区间进行差分，并计数
            cnt++, c[st[i]]++, c[ed[i]]++, c[lca[i]]-=2;
    if(cnt==0)return 1;//没有超过的
    dfs2(1);//求出被经过cnt次，且最长的边
    return maxl-max_edge <= mid;
}
int main(){
    scanf("%d%d", &n, &m);
    for(int i=1; i<n; i++){
        int u, v, w; scanf("%d%d%d", &u, &v, &w);
        Insert(u, v, w); Insert(v, u, w);
    }
    dfs(1);
    for(int i=1; i<=m; i++){
        scanf("%d%d", &st[i], &ed[i]);
        lca[i] = Lca(st[i], ed[i]);
        len[i] = getdis(i);
        maxl = max(maxl,len[i]);
    }
    int l = 0, r = maxl;//最短时间在[0,maxl]之间
    while(l <= r){
        int mid = (l+r)>>1;
        if(check(mid)) ans = mid, r = mid-1;
        else l = mid+1;
    }
    printf("%d\n",ans);
    return 0;
}