距离咨询[tarjan求lca]
农夫约翰有N(2<=N<=40000)个农场,标号1到N。M(2<=M<=40000)条的不同的垂直或水平的道路连结着农场,道路的长度不超过1000.这些农场的分布就像下面的地图一样,图中农场用F1..F7表示:
每个农场最多能在东西南北四个方向连结4个不同的农场。此外,农场只处在道路的两端。道路不会交叉而且每对农场间有且仅有一条路径。邻居鲍伯要约翰来导航,但约翰丢了农场的地图,他只得从电脑的备份中修复率。每一条道路的信息如下:
从农场23往南经距离10到达农场17
从农场1往东经距离7到达农场17
. . .
最近美国过度肥胖非常普遍。农夫约翰为了让他的奶牛多做运动,举办了奶牛马拉松。马拉松路线要尽量长。
奶牛们拒绝跑马拉松,因为她们悠闲的生活无法承受约翰选择的如此长的赛道。因此约翰决心找一条更合理的赛道。他打算咨询你。读入地图之后会有K个问题,每个问题包括2个整数,就是约翰感兴趣的2个农场的编号,请尽快算出这2个农场间的距离。
输入格式
第1行:两个分开的整数N和M。
第2到M+1行:每行包括4个分开的内容,F1,F2,L,D分别描述两个农场的编号,道路的长度,F1到F2的方向N,E,S,W。
第2+M行:一个整数K(1<=K<=10000).
第3+M到2+M+K行:每行输入2个整数,代表2个农场。
输出格式
对每个问题,输出单独的一个整数,给出正确的距离。
样例
样例输入
7 6
1 6 13 E
6 3 9 E
3 5 7 S
4 1 3 N
2 4 20 W
4 7 2 S
3
1 6
1 4
2 6
样例输出
13
3
36
思路
注意到每两个农场间只有一条路相连. 那就是一棵树, 至于方向, 完全没有意义,在读入时直接忽略即可
两个节点间的最短路, 就可以用lca求, 这里我们用tarjan求lca:
我们需要两个边表, 一个存储原图, 一个存储询问.
看注释吧
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 80005;
int n, m, head[maxn], len=-1, dfn[maxn], tot=-1, headq[maxn], vis[maxn], dis[maxn], f[maxn];
struct edge{
int to, nx, w;
}e[maxn], q[maxn];
void add(int x, int y, int w){//建图
e[++len].to = y;
e[len].nx = head[x];
e[len].w = w;
head[x] = len;
e[++len].to = x;
e[len].nx = head[y];
e[len].w = w;
head[y] = len;
}
void add_que(int u, int v){//存储询问
q[++tot].to = v;
q[tot].nx = headq[u];
headq[u] = tot;
q[++tot].to = u;
q[tot].nx = headq[v];
headq[v] = tot;
}
void init(int n){//初始化
for(int i=0; i<=n; i++) f[i] = i;//并查集初始化
memset(vis,0,sizeof(vis));
memset(dis,0,sizeof(dis));
memset(head,-1,sizeof(head));
memset(headq,-1,sizeof(headq));
}
int find(int x){//并查集求祖先
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
void tarjan(int root){
vis[root] = 1;//标记访问
f[root] = root;//初始化父亲
for(int i=head[root]; ~i; i=e[i].nx){//遍历子节点
int v = e[i].to;//子节点
if(!vis[v]){//如果没访问过
dis[v] = dis[root] + e[i].w;//子节点到根节点距离=父节点到根节点距离+边权
tarjan(v);//递归子节点
f[v] = root;//更新父亲
}
}
for(int i=headq[root]; ~i; i=q[i].nx){//处理以当前根节点为起点的询问
int v = q[i].to;//终点
if(vis[v]){//如果已经计算过了
q[i].w = dis[root] + dis[v] - 2*dis[find(v)];//这次询问的距离=起点到祖先的距离+终点到祖先的距离-2*起点终点lca到祖先的距离
q[i^1].w = q[i].w;
}
}
}
int main(){
scanf("%d%d", &n, &m);
init(n);
for(int i=1; i<=m; i++){
int f1, f2, l; scanf("%d%d%d%*c%*c", &f1, &f2, &l);//方向是无用的,直接忽略
add(f1, f2, l);
}
int k; scanf("%d", &k);
for(int i=1; i<=k; i++){
int u, v; scanf("%d%d", &u, &v);
add_que(u, v);
}
tarjan(1);
for(int i=0; i<tot; i+=2) printf("%d\n", q[i].w);
return 0;
}
在这里我解释一下为什么find(v)就可以求出lca
看这个图.
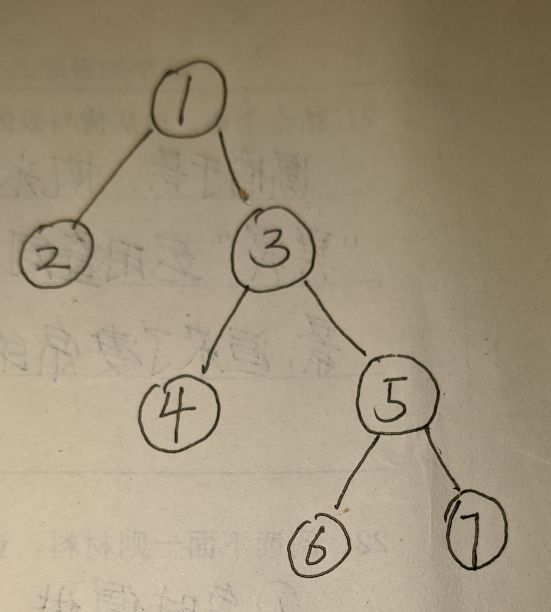
假如我们求4 , 7 间的最短路.
在我们tarjan的时候, 只有根节点的子树都tarjan完时,才会更新他并查集父节点.当我们tarjan(7)时,发现有和7有关的询问,并且4已经访问过, 这时f[3]仍为3, find(3) 就是3, 即lca, 假如4还有子树的话, tarjan(7)时4这边的子树已经访问完, fa[3]已经更新, 所以, 我们可以这样求出lca


