[NOIP2016]天天爱跑步
[NOIP2016]天天爱跑步
题目
小C同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。
这个游戏的地图可以看作一棵包含n个结点和n-1条边的树,每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从1到n的连续正整数。
现在有m个玩家,第i个玩家的起点为Si,终点为Ti。每天打卡任务开始时,所有玩家在第0秒同时从自己的起点出发,以每秒跑一条边的速度,不间断地沿着最短路径向着自己的终点跑去,跑到终点后该玩家就算完成了打卡任务。(由于地图是一棵树,所以每个人的路径是唯一的)
小C想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。 在结点的观察员会选择在第Wj秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第Wj秒也理到达了结点J 。 小C想知道每个观察员会观察到多少人?
注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一 段时间后再被观察员观察到。 即对于把结点J作为终点的玩家: 若他在第Wj秒重到达终点,则在结点J的观察员不能观察到该玩家;若他正好在第Wj秒到达终点,则在结点的观察员可以观察到这个玩家。
INPUT
第一行有两个整数n和m。其中n代表树的结点数量,同时也是观察员的数量,m代表玩家的数量。
接下来n-1行每行两个整数u和v,表示结点u到结点v有一条边。
接下来一行n个整数,其中第j个整数为Wj,表示结点j出现观察员的时间。
接下来m行,每行两个整数Si和Ti,表示一个玩家的起点和终点。
对于所有的数据,保证1≤Si,Ti≤n,0≤ Wj ≤n。
OUTPUT
输出1行n个整数,第j个整数表示结点j的观察员可以观察到多少人。
SAMPLE
INPUT1
6 3
2 3
1 2
1 4
4 5
4 6
0 2 5 1 2 3
1 5
1 3
2 6
OUTPUT1
2 0 0 1 1 1
INPUT2
5 3
1 2
2 3
2 4
1 5
0 1 0 3 0
3 1
1 4
5 5
OUTPUT2
1 2 1 0 1
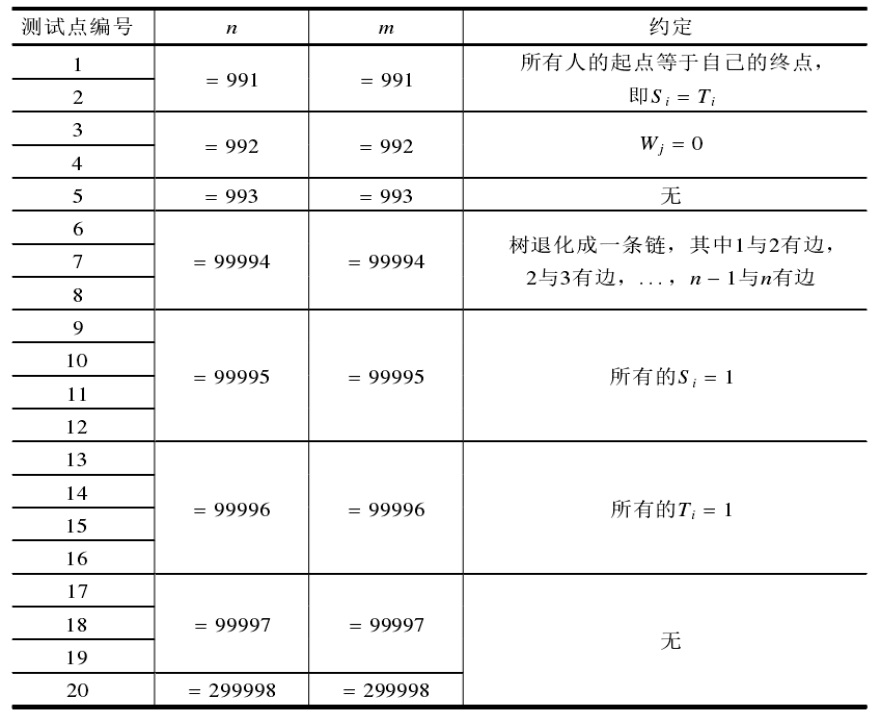
范围
解题报告
从今天下午做到晚上,终于A了= =(明明是从去年做到现在吧啊喂)
设$deep[]$表示节点的深度,$watch[]$表示观察者的出现时间,$s$表示玩家起点,$t$表示终点
首先,只有满足 观察者出现时间=玩家起点与观察者距离 的玩家才对观察者有贡献
显然,在树上的问题,我们很容易想到把路径拆成从起点向上跑到$lca$的路径和$lca$的子节点向下跑到终点的两条路径
对于向上跑的,如果玩家能被观察者$i$观察到,那么一定满足:
$$deep[s]-deep[i]=watch[i]$$
对于向下跑的,如果玩家能被观察者$i$观察到,那么一定满足:
$$deep[s]+deep[i]-2\times deep[lca(s,i)]=watch[i]$$
(显然这两个式子都是由“观察者出现时间=玩家起点与观察者距离”推出来的)
等号左边是玩家起点与观察者的距离,等号右边是观察者出现时间
我们先分析向上跑的——路径:从起点向上跑到$lca$
将式子移项可以得到:
$$deep[s]=deep[i]+watch[i]$$
我们知道$deep[i]$与$watch[i]$都是定值,也就是说,对于观察者$i$,他能观察到的向上跑的玩家,是所有起点=$deep[i]+watch[i]$的玩家
而向上跑还能经过$i$的,一定在$i$的子树中
所以,我们知道,以$i$为根的子树中,所以深度为$deep[i]+watch[i]$的玩家都能被$i$观察到
那么我们搞一个$dfs$序,就能把树上的问题转化为区间上的问题了
深度怎么处理呢?
我们对每一层深度建一棵线段树(此时我们需要动态开点(第一棵动态开点线段树,快打死我了)),那么剩下的就很好解决了
我们将问题转化为了在深度为$deep[i]+watch[i]$的线段树中,查询区间$[a,b]$的玩家个数
玩家个数自然很好处理,瞎XX差分一下就可以了
差分:
在起点处$+1$
在$lca$父节点处$-1$
为什么?
这是差分的惯用思想(科普差分):
我们考虑一个大区间,一开始我们全赋为0,然后我们插入一个区间,将左端点$+1$,右端点后面一个点$-1$,那么在该区间前面的点,显然不受影响,在该区间中的点,我们进行求前缀和处理,我们只能求到左端点的$+1$,而不会求到右端点的$-1$,所以该区间可以被算上,在该区间后的点,我们再求一下前缀和,左端点的$+1$与右端点的$-1$相抵消,对其没有影响(在计算时,它也不会被算在该区间里)
从$lca$的子节点向下跑到终点的同理
把式子移项可得:
$$deep[s]-2\times deep[lca(s,i)]=watch[i]-deep[i]$$
然后$watch[i]$和$deep[i]$仍然是定值,所以我们在深度为$deep[s]-2\times deep[lca(s,i)]$的线段树里进行差分,终点处$+1$,$lca$处$-1$
查询深度为$watch[i]-deep[i]$的线段树即可
-----update-----
动态开点线段树:
注意到,我们在每个深度都开了一棵线段树,所以,我们不可能像以前一样,直接开一大圈线段树,那样内存一定会炸,所以我们可以先开出足够的数组,然后,当我们需要一棵新的线段树时,只需要增加一个新的根节点即可,同样的,当我们需要一个新节点时,我们不需要像以前打线段树一样,去找父节点编号$\times 2$什么的,我们直接在最后开出的节点后面加一个节点,并将它的父节点的儿子指针指向该节点,这样,就可以省去那些一言不合就$\times 2$的下标了,同样,也可以省去许多会让你$MLE$的内存
-----update over-----
细节处理:
- 做完向上跑的玩家后,清空线段树
- 向下跑的$deep[s]-2\times deep[lca(s,i)]$可能出负数,所以全体后移,数组大小要开大一些
- 不会动态开点的先学习一下,不要像我一样作死的以为随便打打就好了= =

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 using namespace std; 5 inline int read(){ 6 int sum(0); 7 char ch(getchar()); 8 for(;ch<'0'||ch>'9';ch=getchar()); 9 for(;ch>='0'&&ch<='9';sum=sum*10+(ch^48),ch=getchar()); 10 return sum; 11 } 12 struct edge{ 13 int e; 14 edge *n; 15 edge():e(0),n(NULL){} 16 }a[600005],*pre[300005]; 17 int tot; 18 inline void insert(int s,int e){ 19 a[++tot].e=e; 20 a[tot].n=pre[s]; 21 pre[s]=&a[tot]; 22 } 23 struct que{ 24 int s,e,lca; 25 }peo[300005]; 26 int n,m; 27 int cnt; 28 int dep[300005],fa[20][300005],id[300005],out[300005]; 29 inline void dfs(int u){ 30 id[u]=++cnt; 31 for(int i=1;(1<<i)<=dep[u];++i) 32 fa[i][u]=fa[i-1][fa[i-1][u]]; 33 for(edge *i=pre[u];i;i=i->n){ 34 int e(i->e); 35 if(e!=fa[0][u]){ 36 fa[0][e]=u; 37 dep[e]=dep[u]+1; 38 dfs(e); 39 } 40 } 41 out[u]=cnt; 42 } 43 inline int lca(int x,int y){ 44 if(dep[x]<dep[y]) 45 swap(x,y); 46 int delta(dep[x]-dep[y]); 47 for(int i=0;delta>0;++i) 48 if((1<<i)&delta){ 49 delta^=1<<i; 50 x=fa[i][x]; 51 } 52 if(x==y) 53 return x; 54 for(int i=19;i>=0;--i) 55 if(fa[i][x]!=fa[i][y]) 56 x=fa[i][x],y=fa[i][y]; 57 return fa[0][x]; 58 } 59 int dfn; 60 int sum[7500005],lc[7500005],rc[7500005],root[1200005]; 61 inline void update(int l,int r,int pos,int w,int &now){ 62 if(!pos) 63 return; 64 if(!now) 65 now=++dfn; 66 sum[now]+=w; 67 if(l==r) 68 return; 69 int mid((l+r)>>1); 70 if(pos<=mid) 71 update(l,mid,pos,w,lc[now]); 72 else 73 update(mid+1,r,pos,w,rc[now]); 74 } 75 inline int query(int l,int r,int ll,int rr,int now){ 76 if(!now) 77 return 0; 78 if(ll<=l&&r<=rr) 79 return sum[now]; 80 int mid((l+r)>>1); 81 int ret(0); 82 if(rr<=mid) 83 return query(l,mid,ll,rr,lc[now]); 84 else 85 if(ll>mid) 86 return query(mid+1,r,ll,rr,rc[now]); 87 else 88 return query(l,mid,ll,mid,lc[now])+query(mid+1,r,mid+1,rr,rc[now]); 89 /* if(ll<=mid) 90 ret+=query(l,mid,ll,rr,lc[now]); 91 if(mid<rr) 92 ret+=query(mid+1,r,ll,rr,rc[now]);*/ 93 } 94 inline void clear(){ 95 dfn=0; 96 memset(lc,0,sizeof(lc)); 97 memset(rc,0,sizeof(rc)); 98 memset(sum,0,sizeof(sum)); 99 memset(root,0,sizeof(root)); 100 } 101 int ans[300005]; 102 int w[300005]; 103 inline int gg(){ 104 freopen("runninga.in","r",stdin); 105 freopen("runninga.out","w",stdout); 106 memset(pre,NULL,sizeof(pre)); 107 n=read(),m=read(); 108 for(int i=1;i<n;++i){ 109 int x(read()),y(read()); 110 insert(x,y),insert(y,x); 111 } 112 dfs(1); 113 for(int i=1;i<=n;++i) 114 w[i]=read(); 115 for(int i=1;i<=m;++i) 116 peo[i].s=read(),peo[i].e=read(),peo[i].lca=lca(peo[i].s,peo[i].e); 117 for(int i=1;i<=m;++i){ 118 int de(dep[peo[i].s]); 119 update(1,n,id[peo[i].s],1,root[de]); 120 update(1,n,id[fa[0][peo[i].lca]],-1,root[de]); 121 } 122 for(int i=1;i<=n;++i) 123 ans[i]+=query(1,n,id[i],out[i],root[dep[i]+w[i]]); 124 clear(); 125 for(int i=1;i<=m;++i){ 126 int de(dep[peo[i].s]-(dep[peo[i].lca]<<1)+(n<<1)); 127 update(1,n,id[peo[i].e],1,root[de]); 128 update(1,n,id[peo[i].lca],-1,root[de]); 129 } 130 for(int i=1;i<=n;++i) 131 ans[i]+=query(1,n,id[i],out[i],root[w[i]-dep[i]+(n<<1)]); 132 for(int i=1;i<=n;++i) 133 printf("%d ",ans[i]); 134 return 0; 135 } 136 int K(gg()); 137 int main(){;}
花絮?
我:哇,为什么全WA了
同桌:哪有全WA,你看还有15个T呢
我:去去去,我从去年做到现在,去年还能拿点分,为啥现在连分都拿不了了
同桌:哇,我A了5个点
我:剩下的呢
同桌:全T了
我:快拿cena跑一跑
同桌:哇,我A了
我:多快?
同桌:100秒= =
(一下午就这样过去了)
我:哇,我A了,你还差多少
同桌:还差一点
(几分钟过去了)
我:哇,你要A了
同桌:咦,怎么WA了一个
我:是不是数组开小了
同桌:唔,好像是,我回去开大点
(又是几分钟过去了)
我:A了?
同桌:嗯
我:咋WA的
同桌:数组开小了
我:那咋WA那么多次
同桌:我不知道动态开点咋搞啊QAQ
然后就有了上面的细节处理= =