[GDOI2014]拯救莫莉斯

[GDOI2014]拯救莫莉斯

题目

莫莉斯·乔是圣域里一个叱咤风云的人物，他凭借着自身超强的经济头脑，牢牢控制了圣域的石油市场。

圣域的地图可以看成是一个n*m的矩阵。每个整数坐标点(x , y)表示一座城市（1<=x<= n, 1<=y<=m）。两座城市间相邻的定义为：对于城市(Ax, Ay)和城市(Bx, By)，满足(Ax - Bx)2 + (Ay - By)2 = 1。

由于圣域的石油贸易总量很大，莫莉斯意识到不能让每笔石油订购单都从同一个油库里发货。为了提高效率，莫莉斯·乔决定在其中一些城市里建造油库，最终使得每一个城市X都满足下列条件之一：

1.该城市X内建有油库，

2.某城市Y内建有油库，且城市X与城市Y相邻。

与地球类似，圣域里不同城市间的地价可能也会有所不同，所以莫莉斯想让完成目标的总花费尽可能少。如果存在多组方案，为了方便管理，莫莉斯会选择建造较少的油库个数。

INPUT

第一行两个正整数n,m ( n * m <= 50 且m<=n)，表示矩阵的大小。

接下来一个n行m列的矩阵F，Fi, j表示在城市(i,j)建造油库的代价。

OUTPUT

输出两个数，建造方案的油库个数和方案的总代价。

SAMPLE

INPUT

3 3

6 5 4

1 2 3

7 8 9

OUTPUT

3 6

解题报告

考试打的爆搜，本来能骗35分的，结果生给CE（编译错误）掉了，重要的是本机跑啥事没有，简直了

正解：

一看数据范围就知道是状压

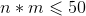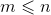首先分析数据范围，且，显然可以推出，那么剩下的就很好办了，我们可以压每一行的状态

然后我们再看，第i行的状态只会对第i-1行至第i+1行产生影响

那么我们就只需要记录一下每一行和它上一行的状态就可以了

设：f[i][j][k]为对于前i行，第i-1行状态为j，第i行状态为k，对于任何一行x（x<i），该行的所有城市都能被供油的情况下，其所能达到的最小代价。

设：g[i][j][k]记录在上述条件下对应f[i][j][k]方案里的油库数量

然后我们可以预处理出每一行的状态所对应的代价与油库数量（设cost[i][j]为第i行，状态为j时所需代价，num[i][j]为第i行状态为j时的油库数量）

那么我们可以很轻松的写出状态转移方程：

f[i+1][k][l]=f[i][j][k]+cost[i+1][l];
g[i+1][k][l]=g[i][j][k]+num[i+1][l];

而其中，l状态可取，需使第i行的所有城市满足要求，即：

((j|l|k|(k<<1)|(k>>1))&(bin[m]-1))==bin[m]-1

那么答案就是 max(f[n+1][x][0]) 

这里需要注意的是，数组不能卡着数开，因为我们的答案存储在n+1中，所以最好多开一点，以防越界

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
inline int read(){
    int sum(0);
    char ch(getchar());
    for(;ch<'0'||ch>'9';ch=getchar());
    for(;ch>='0'&&ch<='9';sum=sum*10+(ch^48),ch=getchar());
    return sum;
}
int n,m;
int bin[8];
int w[55][10];
int g[55][1<<7][1<<7],f[55][1<<7][1<<7],cost[55][1<<7],num[55][1<<7];
int main(){
//  freopen("proj.in","r",stdin);
//  freopen("proj.out","w",stdout);
    memset(f,30,sizeof(f));
    memset(cost,0,sizeof(cost));
    bin[0]=1;
    for(int i=1;i<8;i++)
        bin[i]=bin[i-1]<<1;
    n=read(),m=read();
    for(int i=1;i<=n;i++)
        for(int j=0;j<m;j++)
            w[i][j]=read();
    for(int i=1;i<=n;i++)
        for(int j=0;j<bin[m];j++)
            for(int k=0;k<m;k++)
                if(bin[k]&j){
                    cost[i][j]+=w[i][k];
                    num[i][j]++;
                }
/*  for(int i=1;i<=n;i++)
        for(int j=0;j<bin[m];j++)
            cout<<i<<' '<<j<<' '<<cost[i][j]<<endl;*/
    for(int i=0;i<bin[m];i++)
        f[0][i][0]=0;
    for(int i=0;i<=n;i++)
        for(int j=0;j<bin[m];j++)
            for(int k=0;k<bin[m];k++)
                for(int l=0;l<bin[m];l++){
                    if(((j|l|k|(k<<1)|(k>>1))&(bin[m]-1))!=bin[m]-1)
                        continue;
                    if(f[i+1][k][l]>f[i][j][k]+cost[i+1][l]){//cout<<i<<endl;
                        f[i+1][k][l]=f[i][j][k]+cost[i+1][l];
                        g[i+1][k][l]=g[i][j][k]+num[i+1][l];//cout<<i<<" "<<i+1<<' '<<k<<' '<<l<<' '<<f[i+1][k][l]<<endl;
                    }
                }
    int ans(0x7fffffff),ji;//cout<<m<<' '<<bin[m]<<endl;
    for(int i=0;i<bin[m];i++){//cout<<i<<" "<<f[n+1][i][0]<<endl;
        if(f[n+1][i][0]==ans)
            if(ji>g[n+1][i][0])
                ji=g[n+1][i][0];
        if(f[n+1][i][0]<ans){//cout<<i<<' '<<f[n+1][i][0]<<endl;
            ans=f[n+1][i][0];
            ji=g[n+1][i][0];
        }
    }
    printf("%d %d",ji,ans);
}