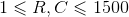[Codeup 25481] swan
[Codeup 25481] swan
题目
两头白天鹅生活在一个部分湖面结了冰的湖泊中,湖面的形状为一个长方形,并且被分割成R行C列的小方格,某些方格中结了冰,这样的方格称之为冰格,其余的方格称之为水格。冬天过去了,湖面上的冰渐渐开始溶解了,每一天与水相邻的冰格就将消融而转化为水格。所谓两个方格相邻是指它们在水平或垂直方向有公共边,两个呈对角的方格是不相邻的,下图给出样例数据的演化过程。
白天鹅只能在水中沿水平或垂直方向游动,写一个程序判断多少天后两只白天鹅才能够相会。
INPUT
输入文件第一行包含两个用空格隔开的整数R和C,其中1 ≤ R, C ≤ 1500,接下来的R行每行包含C个字符,描述湖面的初始状态,‘·’表示水格,‘ X’表示冰格,‘ L’表示一只白天鹅。
OUTPUT
输出文件仅一行包含一个整数表示两只白天鹅等到相邻那一天所需的天数。
SAMPLE
INPUT
8 17
...XXXXXX..XX.XXX
....XXXXXXXXX.XXX
...XXXXXXXXXXXX..
..XXXXX.LXXXXXX..
.XXXXXX..XXXXXX..
XXXXXXX...XXXX...
..XXXXX...XXX....
....XXXXX.XXXL...
OUTPUT
2
范围
30%数据
100%其中
解题报告
考试时打了个奇奇怪怪的dfs= =
正解:
两遍bfs
首先,我们要处理出每一块冰什么时候会化(或者说每一块什么时候可以走)。我们先把所有一开始水的点(包括俩天鹅)压入队列,并将time值赋为0,。接下来进行bfs,就可以处理出来每个点融化的时间(注意要标记,不然时间会出问题)
接着,我们再进行一次bfs,这次是处理出从其中一只天鹅到其他点最短的时间(其实相当于一次SPFA,只不过SPFA是处理出路径长度和,这个bfs是处理出使最长的时间最短的路径)。这里需要注意的是,决不能将某点的最短时间处理的比融化时间还要短,这肯定是不合法的(显然,某点还未融化,自然不可能到达)
最后直接输出到另一只天鹅所需最短时间即可。

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 using namespace std; 5 int head,tail; 6 struct node{ 7 int x,y; 8 }q[20000005]; 9 inline char read(){ 10 char ch(getchar()); 11 for(;ch!='X'&&ch!='L'&&ch!='.';ch=getchar()); 12 return ch; 13 } 14 int dis[1505][1505]; 15 int tim[1505][1505]; 16 bool vis[1505][1505]; 17 int r,c; 18 int x1,y1,x2,y2; 19 int main(){ 20 // freopen("swan.in","r",stdin); 21 // freopen("swan.out","w",stdout); 22 memset(dis,0x3f,sizeof(dis)); 23 memset(tim,0x3f,sizeof(tim)); 24 scanf("%d%d",&r,&c); 25 head=tail=0; 26 for(int i=1;i<=r;i++) 27 for(int j=1;j<=c;j++){ 28 char ch(read()); 29 if(ch=='.'){ 30 tim[i][j]=0; 31 q[++tail]=(node){i,j}; 32 vis[i][j]=1; 33 } 34 if(ch=='L'){ 35 tim[i][j]=0; 36 q[++tail]=(node){i,j}; 37 vis[i][j]=1; 38 if(!x1) 39 x1=i,y1=j; 40 else 41 x2=i,y2=j; 42 } 43 } 44 while(head<tail){ 45 node k(q[++head]); 46 int x(k.x),y(k.y);//cout<<head<<' '<<tail<<' '<<x<<' '<<y<<endl; 47 if(x!=1&&!vis[x-1][y]&&tim[x][y]+1<tim[x-1][y]) 48 tim[x-1][y]=tim[x][y]+1,vis[x-1][y]=1,q[++tail]=(node){x-1,y}; 49 if(x!=r&&!vis[x+1][y]&&tim[x][y]+1<tim[x+1][y]) 50 tim[x+1][y]=tim[x][y]+1,vis[x+1][y]=1,q[++tail]=(node){x+1,y}; 51 if(y!=1&&!vis[x][y-1]&&tim[x][y]+1<tim[x][y-1]) 52 tim[x][y-1]=tim[x][y]+1,vis[x][y-1]=1,q[++tail]=(node){x,y-1}; 53 if(y!=c&&!vis[x][y+1]&&tim[x][y]+1<tim[x][y+1]) 54 tim[x][y+1]=tim[x][y]+1,vis[x][y-1]=1,q[++tail]=(node){x,y+1}; 55 } 56 memset(vis,0,sizeof(vis)); 57 head=tail=0; 58 dis[x1][y1]=0; 59 q[++tail]=(node){x1,y1}; 60 /*for(int i=1;i<=r;i++) 61 for(int j=1;j<=c;j++) 62 if(tim[i][j]==0) 63 q[++tail]=(node){i,j},vis[i][j]=1;*/ 64 while(head<tail){ 65 node k(q[++head]); 66 int x(k.x),y(k.y); 67 vis[x][y]=0;//cout<<x<<' '<<y<<' '<<tim[x][y]<<' '<<dis[x][y]<<endl; 68 if(x!=1&&dis[x][y]<dis[x-1][y]&&dis[x-1][y]!=tim[x-1][y]){ 69 dis[x-1][y]=max(dis[x][y],tim[x-1][y]); 70 if(!vis[x-1][y]){ 71 vis[x-1][y]=1; 72 q[++tail]=(node){x-1,y}; 73 } 74 } 75 if(x!=r&&dis[x][y]<dis[x+1][y]&&dis[x+1][y]!=tim[x+1][y]){ 76 dis[x+1][y]=max(dis[x][y],tim[x+1][y]); 77 if(!vis[x+1][y]){ 78 vis[x+1][y]=1; 79 q[++tail]=(node){x+1,y}; 80 } 81 } 82 if(y!=1&&dis[x][y]<dis[x][y-1]&&dis[x][y-1]!=tim[x][y-1]){ 83 dis[x][y-1]=max(dis[x][y],tim[x][y-1]); 84 if(!vis[x][y-1]){ 85 vis[x][y-1]=1; 86 q[++tail]=(node){x,y-1}; 87 } 88 } 89 if(y!=c&&dis[x][y]<dis[x][y+1]&&dis[x][y+1]!=tim[x][y+1]){ 90 dis[x][y+1]=max(dis[x][y],tim[x][y+1]); 91 if(!vis[x][y+1]){ 92 vis[x][y+1]=1; 93 q[++tail]=(node){x,y+1}; 94 } 95 } 96 } 97 /* for(int i=1;i<=r;i++){ 98 for(int j=1;j<=c;j++) 99 cout<<dis[i][j]<<' '; 100 cout<<endl; 101 }*/ 102 printf("%d",dis[x2][y2]); 103 }