「虚树」学习笔记
虚树
虚树的定义
虚树:将树上有用的节点建立新的图,而舍去关键节点之间的没有用处的节点
虚树的用途:对于一些有关键点的图而言,其余没有用处的节点在操作的时候会作出很多的冗余操作,时间效率大大降低,而利用虚树建图就可以舍去没有用的操作
前置知识1:\(dfs\)序
\(dfs\)序,顾名思义,就是在对图做\(dfs\)的时候的顺序。
举个例子:

该图中节点就是按\(dfs\)序编号的
我们可以利用\(dfs\)序找到一些很有用的性质:
1.\(dfs\)序较大的有两种情况,一种是\(dfs\)序大的在\(dfs\)序小的的子树中,另一种是两个点不再一颗子树中(好像是废话,树上的点不都是这样吗)。
2.\(dfs\)序有连续性,在一个\(dfs\)序小的节点后一段都在该节点的子树中,在后面的建图中用处很大。
来道例题(\(CF613D\; Kingdom \; and\; its \;Cities\))
题意:给定一棵树, \(q\) 组询问,每组询问给定 \(k\) 个点,你可以删掉不同于那 \(k\) 个点的 \(m\) 个点,使得这 \(k\) 个点两两不连通,要求最小化 \(m\),如果不可能输出 −1。询问之间独立。
思路:
首先如果两个节点都是关键点,并且两个点相邻,那么就是无解的情况,否则都有解。那么怎么求最小的 \(m\) 呢?
一种方法可以暴力遍历全图,两个节点之间只断一个点,选择那种可以切掉一个点可以将多个点都断开连接的,比如这种:
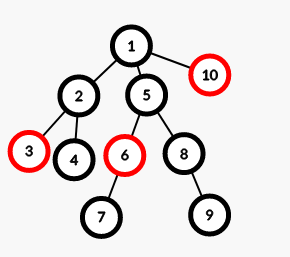
我们只把1节点删去就可以达到所有点都不联通的目的。
暴力做的话,时间复杂度并不是很优秀。我们考虑只用关键点和一些必要的公共祖先去建树,那么虚树的关键就在于如何去利用 \(dfs\) 序建图。
首先对于关键点用 \(dfs\) 序排序,如果根节点不是关键点,把根节点也加进去。
当栈为空或栈中只有一个元素(即 \(top\) <=1, \(top\) 从0开始),直接把x压入栈中
维护一个栈,显然 \(dfs\) 序小的节点先进栈,记住, \(dfs\) 序小的在栈底。
如果 \(dfs\) 序大的节点在 \(dfs\) 序小的节点(即栈顶)的子树中,那么就直接扔进栈里。
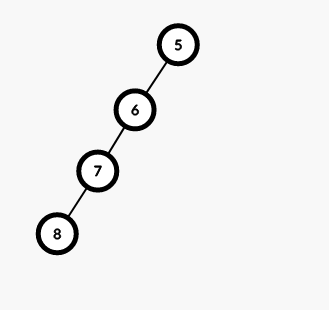
否则该节点就是在新的子树中,是这种情况:
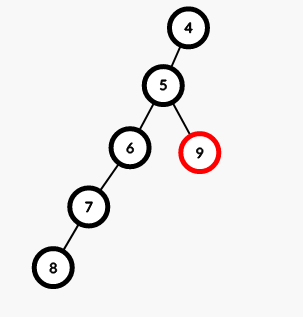
判断依据就是看将当前点和栈顶的 \(lca\) 是不是栈顶元素,也就是图中当前节点9和栈顶节点8的 \(lca\) 是不是8,如果是,那么就直接推进栈里;
不是的话,说明 \(x\) 和 \(stk[top]\) 分属 \(lca\) 的两棵不同的子树,而且\(stk[top]\)所在的子树中已经构建完成了。所以我们把 \(lca\) 的 \(stk[top]\) 所在的子树弹栈,在弹栈的过程中建边,直到 \(dfn[stk[top]]<=dfn[lca]<=dfn[stk[top-1]]\)(即\(lca\)在栈顶的两元素的路径上),或者栈内的元素小于两个,可以自己模拟一下。
此时我们看\(lca\)是不是栈顶元素,如果是的话,将当前节点进栈,如果不是的话,从栈顶向\(lca\)连边,弹出栈顶,将\(lca\)压进栈,并将当前节点也进栈。
在枚举完关键点后,将栈内剩余元素都建边,弹栈。此时虚树已经建好了,就可以用之前的做法在虚树上操作了。
建图代码(细品):
inline void ins(int x){
if (tp == 0){
stk[tp = 1] = x;
return;
}
int LCA = lca(stk[tp], x);
while ((tp > 1) && (deep[LCA] < deep[stk[tp - 1]])) {
addedge(stk[tp - 1], stk[tp]);
--tp;
}
if (deep[LCA] < deep[stk[tp]]) addedge(LCA, stk[tp--]);
if ((!tp) || (stk[tp] != LCA)) stk[++tp] = LCA;
stk[++tp] = x;
}
大体代码实现:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 1e5 + 50;
inline int read () {
int x = 0, f = 1; char ch = getchar();
for (;!isdigit(ch); ch = getchar()) if (ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
return x * f;
}
int n, m, q;
struct Edge {
int to, next;
} edge[maxn << 1];
int tot, head[maxn];
void addedge (int a, int b) {
edge[++tot].to = b;
edge[tot].next = head[a];
head[a] = tot;
}
int siz[maxn], fa[maxn], deep[maxn], son[maxn];
void dfs1 (int u) {
siz[u] = 1;
for (register int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
if (v == fa[u]) continue;
deep[v] = deep[u] + 1;
fa[v] = u;
dfs1 (v);
siz[u] += siz[v];
if (siz[v] > siz[son[u]]) son[u] = v;
}
}
int dfn_clock;
int dfn[maxn], top[maxn];
void dfs2 (int u) {
dfn[u] = ++dfn_clock;
if (son[u]) {
top[son[u]] = top[u];
dfs2 (son[u]);
for (register int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
if (v != fa[u] && v != son[u]) {
top[v] = v;
dfs2 (v);
}
}
}
}
inline int lca (int x, int y) {
while (top[x] != top[y]) {
if (deep[top[x]] > deep[top[y]]) {
x = fa[top[x]];
} else {
y = fa[top[y]];
}
}
if (deep[x] < deep[y]) {
return x;
} else {
return y;
}
}
int tp;
int stk[maxn];
inline void ins(int x) {
if (tp==0) {
stk[tp=1]=x;
return;
}
int ance=lca(stk[tp],x);
while ((tp>1)&&(deep[ance]<deep[stk[tp-1]])) {
addedge(stk[tp-1],stk[tp]);
--tp;
}
if (deep[ance]<deep[stk[tp]]) addedge(ance,stk[tp--]);
if ((!tp)||(stk[tp]!=ance)) stk[++tp]=ance;
stk[++tp]=x;
}
int ans;
int a[maxn];
bool cmp (int a, int b) {
return dfn[a] < dfn[b];
}
void dfs3 (int u) {
if (siz[u]) {
for (register int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
dfs3 (v);
if (siz[v]) {
siz[v] = 0;
ans++;
}
}
} else {
for (register int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
dfs3 (v);
siz[u] += siz[v];
siz[v] = 0;
}
if (siz[u] > 1) {
ans++;
siz[u] = 0;
}
}
}
int main () {
n = read();
int from, to;
for (register int i = 1; i < n; i++) {
from = read(), to = read();
addedge (from, to), addedge(to, from);
}
tot = 0;
top[1] = 1;
deep[1] = 1;
dfs1 (1);
dfs2 (1);
memset (head, 0, sizeof head);
memset (siz, 0, sizeof siz);
tot = 0;
q = read();
while (q--) {
memset (head, 0, sizeof head);
m = read();
for (register int i = 1; i <= m; i++) {
a[i] = read();
siz[a[i]] = 1;
}
bool judge = false;
for (register int i = 1; i <= m; i++) {
if (siz[fa[a[i]]]) {
puts("-1");
judge = true;
break;
}
}
if (judge == true) {
memset (siz, 0, sizeof siz);
continue;
}
ans = 0;
sort (a + 1, a + 1 + m, cmp);
if (a[1] != 1) {
stk[tp = 1] = 1;
}
for (register int i = 1; i <= m; i++) {
ins(a[i]);
}
if (tp) {
while (--tp) {
addedge (stk[tp], stk[tp + 1]);
}
}
dfs3 (1);
memset (siz, 0, sizeof siz);
dfn_clock = 0;
printf ("%d\n", ans);
}
return 0;
}
例题2(凉宫春日的消失)
在观察凉宫和你相处的过程中,\(Yoki\)产生了一个叫做爱的\(bugfeature\),将自己变成了一个没有特殊能力的普通女孩并和你相遇。但你仍然不能扔下凉宫,准备利用\(Yoki\)留下的紧急逃脱程序回到原来的世界。这个紧急逃脱程序的关键就是将线索配对。
为了简化问题,我们将可能的线索间的关系用一棵\(n\)个点的树表示,两个线索的距离定义为其在树上唯一最短路径的长度。因为你不知道具体的线索是什么,你需要进行\(q\)次尝试,每次尝试都会选中一个大小为偶数的线索集合\(V\) ,你需要将线索两两配对,使得配对线索的距离之和不超过\(n\) 。如果这样的方案不存在,输出\(No\) 。
思路
一眼看到选关键点,显然可以用虚树搞,并且很显然有一个性质,该条件只要关键点数是偶数,那么一定存在方案。一个类似贪心的思想,可以在一颗子树中找到配对的就在一颗子树中解决,并且一颗子树中最多只会有一个点没有找到配对,那么把当前点扔到父节点中找配对,并且这个点选最靠上的,具体证明不证了,画画图很显然。
然后每次把关键点建一颗虚树,然后进行上述操作搞搞就好了。
代码实现(为啥我的跑的这么慢\(qwq\))
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int maxn = 2e5 + 50;
inline int read () {
int x = 0, f = 1; char ch = getchar();
for (;!isdigit(ch); ch = getchar()) if (ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
return x * f;
}
int n;
struct Edge {
int from, to, next;
} edge[maxn << 1];
int tot, head[maxn];
inline void addedge (int a, int b) {
edge[++tot].to = b;
edge[tot].from = a;
edge[tot].next = head[a];
head[a] = tot;
}
deque<int> que[maxn];
bool col[maxn];
int f[maxn];
int son[maxn], siz[maxn], deep[maxn];
void dfs1 (int u) {
siz[u] = 1;
for (register int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
if (v == f[u]) continue;
f[v] = u;
deep[v] = deep[u] + 1;
dfs1 (v);
siz[u] += siz[v];
if (siz[v] > siz[son[u]]) son[u] = v;
}
}
int dfn[maxn], dfn_clock;
int top[maxn];
void dfs2 (int u) {
dfn[u] = ++dfn_clock;
if (son[u]) {
top[son[u]] = top[u];
dfs2 (son[u]);
for (register int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
if (v != f[u] && v != son[u]) {
top[v] = v;
dfs2 (v);
}
}
}
}
inline int lca (int x, int y) {
while (top[x] != top[y]) {
if (deep[top[x]] > deep[top[y]]) {
x = f[top[x]];
} else {
y = f[top[y]];
}
}
if (deep[x] < deep[y]) return x;
return y;
}
int tp;
int stk[maxn];
inline void ins(int x)
{
if (tp == 0)
{
stk[tp = 1] = x;
return;
}
int ance = lca(stk[tp], x);
while ((tp > 1) && (deep[ance] < deep[stk[tp - 1]]))
{
addedge(stk[tp - 1], stk[tp]);
--tp;
}
if (deep[ance] < deep[stk[tp]]) addedge(ance, stk[tp--]);
if ((!tp) || (stk[tp] != ance)) stk[++tp] = ance;
stk[++tp] = x;
}
int a[maxn];
inline void dfs (int u) {
stk[++tp] = u;
for (register int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
dfs(v);
if (!que[v].empty()) {
int a = que[v].front();
que[v].pop_front();
que[u].push_back(a);
}
}
if (col[u]) que[u].push_front(u);
while (!que[u].empty()) {
int a = que[u].back();
que[u].pop_back();
if (!que[u].empty()) {
int b = que[u].back();
que[u].pop_back();
printf("%d %d\n", a, b);
} else {
que[u].push_back(a);
break;
}
}
}
bool cmp (int a, int b) {
return dfn[a] < dfn[b];
}
int main () {
n = read();
int x, y;
for (register int i = 1; i < n; i++) {
x = read(), y = read();
addedge (x, y), addedge (y, x);
}
int s;
dfs1 (1);
dfs2 (1);
memset (head, 0, sizeof head);
tot = 0;
while (1) {
s = read();
if (s == 0) return 0;
for (register int i = 1; i <= s; i += 1) {
a[i] = read();
col[a[i]] = true;
}
printf("Yes\n");
sort (a + 1, a + 1 + s, cmp);
if (a[1] != 1) {
stk[tp = 1] = 1;
}
for (register int i = 1; i <= s; i++) {
ins (a[i]);
}
if (tp) {
while (--tp) {
addedge (stk[tp], stk[tp + 1]);
}
}
tp = 0;
dfs (1);
for (register int i = 1; i <= tp + 1; i++) {
head[stk[i]] = 0;
col[stk[i]] = false;
}
tp = 0;
tot = 0;
}
return 0;
}
例题3 (大工程 HEOI2014)
国家有一个大工程,要给一个非常大的交通网络里建一些新的通道。
我们这个国家位置非常特殊,可以看成是一个单位边权的树,城市位于顶点上。
在 2 个国家 a,b 之间建一条新通道需要的代价为树上 a,b 的最短路径。
现在国家有很多个计划,每个计划都是这样,我们选中了 k 个点,然后在它们两两之间 新建 C(k,2)条 新通道。现在对于每个计划,我们想知道:
1.这些新通道的代价和 2.这些新通道中代价最小的是多少 3.这些新通道中代价最大的是多少
数据范围:
对于第 1,2 个点: n<=10000
对于第 3,4,5 个点: n<=100000,交通网络构成一条链
对于第 6,7 个点: n<=100000
对于第 8,9,10 个点: n<=1000000
对于所有数据, q<=50000并且保证所有k之和<=2n
看到数据范围中k之和 <= 2n,显然虚树,建好虚树后就写了一个很朴素的树上dp
记住一定不要memset,一定不要memset,一定不要memset
我是不会说我因为本地机太菜连dfs都跑不出来(其实是我不会开无限栈),也不会说有个nt白建一颗虚树然后五个大数组memset,直接掉到n*q的效率,然后卡了3天还是机房大佬调出来的\(qwq\)
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
const int maxn = 1e6 + 50;
inline int read () {
int x = 0, f = 1; char ch = getchar();
for (;!isdigit(ch); ch = getchar()) if (ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
return x * f;
}
int n, q;
struct Edge {
int from, to, next, val;
} edge[maxn << 2];
int tot, head[maxn << 1];
inline void addedge (int a, int b, int c) {
edge[++tot].to = b;
edge[tot].from = a;
edge[tot].next = head[a];
head[a] = tot;
edge[tot].val = c;
}
int dis[maxn], deep[maxn], fa[maxn][24];
bool col[maxn];
int dfn[maxn], dfn_clock;
inline void dfs1 (int u) {
dfn[u] = ++dfn_clock;
for (register int i = 0; fa[u][i]; i++) {
fa[u][i + 1] = fa[fa[u][i]][i];
}
for (int i = head[u]; i; i = edge[i].next) {
int v = edge[i].to;
if (v == fa[u][0]) continue;
deep[v] = deep[u] + 1;
fa[v][0] = u;
dis[v] = dis[u] + 1;
dfs1 (v);
}
}
int lca(int a, int b){
if(deep[a] < deep[b]){
swap(a, b);
}
register int d = deep[a] - deep[b];
for (int i = 0; d; i++, d >>= 1) {
if(d & 1) a = fa[a][i];
}
if(a == b) return a;
for (int i = 20; i >= 0; i--) {
if(fa[a][i] != fa[b][i]){
a = fa[a][i], b = fa[b][i];
}
}
return fa[a][0];
}
int m, a[maxn];
inline bool cmp (int a, int b) {
return dfn[a] < dfn[b];
}
int tp, stk[maxn << 1];
inline void ins (int x) {
if (tp == 0) {
stk[++tp] = x;
return;
}
register int LCA = lca (stk[tp], x);
while ((tp > 1) && (deep[LCA] < deep[stk[tp-1]])) {
addedge (stk[tp-1], stk[tp], dis[stk[tp-1]] + dis[stk[tp]] - 2 * dis[lca(stk[tp - 1], stk[tp])]);
tp--;
}
if (deep[LCA] < deep[stk[tp]]) {
addedge (LCA, stk[tp--], dis[stk[tp]] + dis[LCA] - 2 * dis[lca (stk[tp], LCA)]);
}
if ((tp == 0) || (stk[tp] != LCA)) stk[++tp] = LCA;
stk[++tp] = x;
}
int maxdis;
long long finalans;
int mindis;
int siz[maxn << 1];
inline void dfs3 (int u, int fa, int diss) {
stk[++tp] = u;
if (col[u]) siz[u] = 1;
for (register int i = head[u]; i; i = edge[i].next) {
register int v = edge[i].to;
if (v == fa) continue;
dfs3 (v, u, diss + edge[i].val);
finalans += 1ll * siz[v] * (m - siz[v]) * edge[i].val;
siz[u] += siz[v];
}
}
int dpmin[maxn << 1], dpmax[maxn << 1];
inline void divdfs (int u, int f) {
if (col[u]) {
dpmin[u] = 0;
for (register int i = head[u]; i; i = edge[i].next) {
register int v = edge[i].to;
if (v == f) continue;
divdfs (v, u);
mindis = min(dpmin[v] + edge[i].val, mindis);
maxdis = max (dpmax[u] + dpmax[v] + edge[i].val, maxdis);
dpmax[u] = max (dpmax[v] + edge[i].val, dpmax[u]);
}
}
else {
int lastmax = 0;
for (register int i = head[u]; i; i = edge[i].next) {
register int v = edge[i].to;
if (v == f) continue;
divdfs (v, u);
if (lastmax != 0) maxdis = max (lastmax + dpmax[v] + edge[i].val, maxdis);
lastmax = max (lastmax, dpmax[v] + edge[i].val);
dpmax[u] = max (dpmax[v] + edge[i].val, dpmax[u]);
mindis = min (mindis, dpmin[u] + dpmin[v] + edge[i].val);
dpmin[u] = min (dpmin[u], dpmin[v] + edge[i].val);
}
}
}
signed main () {
n = read();
int x, y;
for (register int i = 1; i < n; i++) {
x = read(), y = read();
addedge (x, y, 1), addedge (y, x, 1);
}
dfs1 (1);
tot = 0;
q = read();
memset(head,0,sizeof(head));
memset(dpmin,0x3f,sizeof(dpmin));
while (q--) {
m = read();
tot = 0;
for (register int i = 1; i <= m; i++) {
a[i] = read();
col[a[i]] = true;
}
sort (a + 1, a + 1 + m, cmp);
if (a[1] != 1) {
stk[tp = 1] = 1;
}
mindis = 0x3f3f3f3f;
for (register int i = 1; i <= m; i++) {
ins (a[i]);
}
if (tp) {
while (--tp) {
addedge (stk[tp], stk[tp + 1], dis[stk[tp]] + dis[stk[tp + 1]] - 2 * dis[lca(stk[tp + 1], stk[tp])]);
}
}
tp = 0;
maxdis = 0;
finalans = 0;
dfs3 (1, 0, 0);
divdfs(1, 0);
printf ("%lld %d ", finalans, mindis);
printf ("%d\n", maxdis);
for(int i = 1; i <= tp; i++){
siz[stk[i]] = col[stk[i]] = head[stk[i]] = dpmax[stk[i]] = 0;
dpmin[stk[i]] = 0x3f3f3f3f;
}
tp = 0;
}
return 0;
}


