计算几何
首先,我们需要一些向量和坐标系的知识作为铺垫
坐标系中的向量表示及运算
大家应该都对平面直角坐标系有一些认识
向量表示法
向量就是一条有长度有方向的线段。我们可以随意画一条线段,标上箭头就是向量。向量的起点是\(A\)终点是\(B\),那么我们可以表示向量为\(\overrightarrow{AB}\),也可以表示为\(\overrightarrow{a}\)
同时向量具有平移不变性,我们把这样一个有向线段到处平移,向量不变。
用随便画一条线段的方式表示向量有一个非常大的弊端,我们只能直观的看到这个向量,却无法很简便的对它进行量化计算,所以我们把向量放在坐标系中,用坐标来表示向量,由于向量具有平移不变性,所以我们可以把向量的起点平移到原点,这样的话,直接用终点的坐标表示一个向量即可,即用\((x,y)\)表示从\((0,0)\)指向\((x,y)\)的向量
向量的模
即向量的长度,\(\overrightarrow{a}=(x,y)\)表示为\(\sqrt{x^2+y^2}\)
零向量
这这玩意模长(长度)为零,方向任意,在坐标系中表示为(0,0)
认为它与任意向量共线!!!
相反向量
\(\overrightarrow{a}=(x,y)\)的相反向量是\(-\overrightarrow{a}=(-x,-y)\)
平行向量(共线向量)
向量所在直线平行,或者说,一个向量平移后可以与另外一个向量共线
\(\overrightarrow{a}=(x_1,y_1),\overrightarrow{b}=(x_2,y_2)\)
则\(\overrightarrow{a}\)和\(\overrightarrow{b}\)共线的条件是\(\frac{y1}{x1}=\frac{y2}{x2}\)
垂直向量
两个向量所在直线垂直
\(\overrightarrow{a}=(x_1,y_1),\overrightarrow{b}=(x_2,y_2)\)
则\(\overrightarrow{a}\)和\(\overrightarrow{b}\)垂直的条件是\(x_1·x_2+y_1·y_2=0\)
向量加法
\(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{c}\)
通过平移将\(\overrightarrow{a},\overrightarrow{b}\)首尾相接,\(\overrightarrow{c}\)为从\(\overrightarrow{a}\)的起点指向\(\overrightarrow{b}\)的终点的向量
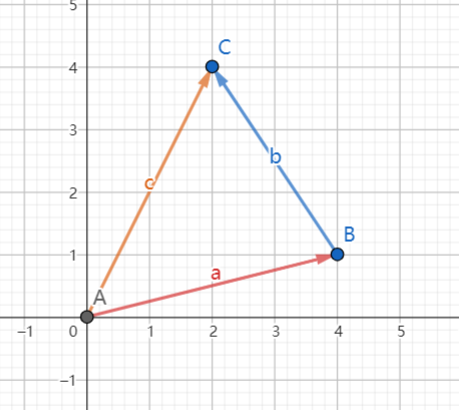
\(\overrightarrow{c}=(x1+x2,y1+y2)\)
向量减法
\(\overrightarrow{c}=\overrightarrow{a}-\overrightarrow{b}\)
通过平移将\(\overrightarrow{a}\)和\(\overrightarrow{b}\)的起点相接,\(\overrightarrow{c}\)为从\(\overrightarrow{b}\)的终点指向\(\overrightarrow{a}\)的终点
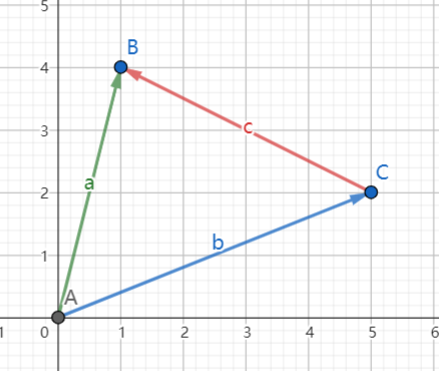
\(\overrightarrow{c}=(x1-x2,y1-y2)\)
也可以理解为\(\overrightarrow{c}=\overrightarrow{a}+(-\overrightarrow{b})\)
向量数乘
就是向量乘上一个数,得到的向量还是一个向量,比如
\(\overrightarrow{a}=(x_1,y_1)\ \ \ ,\ \ \ k\overrightarrow{a}=(kx_1,kx_2)\)
\(k\)可正可负可为零,实际上就是模长的变化,还有反向
向量乘法之点积
向量乘向量有两种,一个是点积,一个是叉积
点积表示为\(\overrightarrow{a}·\overrightarrow{b}=c\)
c是一个数,也就是说,两个向量的点积得到的是一个数,几何意义就是一个向量在另一个向量上的投影的模长乘积,\(\overrightarrow{a}·\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos\theta\),\(\theta\)是两个向量的夹角
因此点积可以用来求向量的投影或者夹角,而且点积具有交换律
在坐标系中表示为\(x_1x_2+y1y2\),还有一些关于点积的性质
若两个向量夹角是锐角,点积为正数
若两个向量互相垂直,点积为0
若两个向量夹角为钝角或180,点积为负数
若两个向量共线,则点积是两个向量的模的乘积
向量乘法之叉积
点积是\(\overrightarrow{a}·\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos\theta\)
那么\(|\overrightarrow{a}||\overrightarrow{b}|sin\theta\)就是另外一种乘法,也就是叉积,表示为\(\overrightarrow{a}\times\overrightarrow{b}\)
实际上叉积得到的是一个向量,这个向量方向符合右手法则,从a握向b,大拇指冲的方向就是向量的方向,大小是\(|\overrightarrow{a}||\overrightarrow{b}|sin\theta\),\(\theta\)是从a沿着逆时针方向旋转到b的旋转角,如果算出来是负数,就是反方向
而我们知道,\(|\overrightarrow{a}||\overrightarrow{b}||sin\theta|\)可以表示两个向量夹成的平行四边形的面积,所以这个叉积用来求面积十分的方便
在坐标系中,叉积同样可以直接用坐标乘积表示\(x_1y_2-x_2y_1\)
因为旋转方向固定,所以叉积与点积不同,叉积没有交换律,交换之后的结果就反向了
同样的分析一些性质,如果a与b平行那么叉积是0,如果b在a左侧(假设起点相同)那么叉积是正的,如果在右侧则是负的,所以这个东西也可以用来判断向量的位置
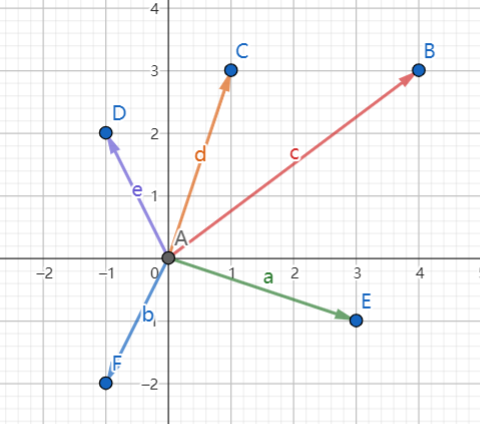
线段交点
这里给出5分钟思考一下,利用叉积也就是面积,怎么求出两条线段所在直线的交点
利用面积与相似就可以求出线段的交点,我们先考虑线段的情况
这里借用一下洛谷日报的图片
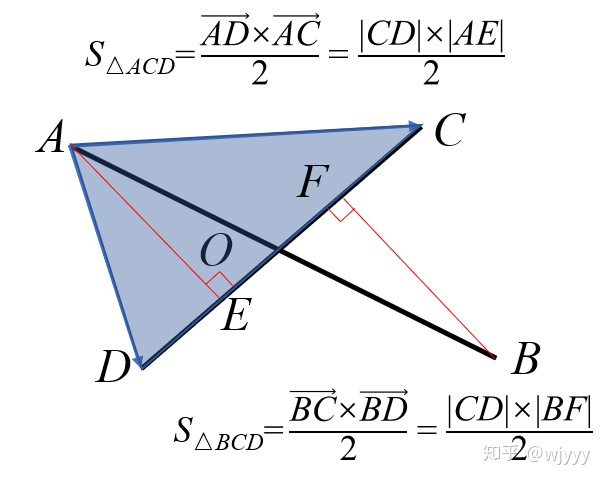
然后利用ACD和ABCD的面积之比就可以求得AO与AB的比值,由于已经有了A的位置和向量AB,就可以得到O的位置了
这个公式可以直接用叉积表示出来
\(\overrightarrow{AO}=\frac{S_{ACD}}{S_{ABCD}} *\overrightarrow{AB}=\frac{\frac{\overrightarrow{AC}\times\overrightarrow{AB}}{2}}{\frac{\overrightarrow{AB}\times\overrightarrow{CD}}{2}}*\overrightarrow{AB}\)
这里直接用就可以,即使是所在直线的交点,也可以求出来,因为面积求出来时候也带着正负,结合之后就恰好得到交点
多边形面积
我们利用三角剖分求多边形面积,首先是一种比较简单的凸多边形
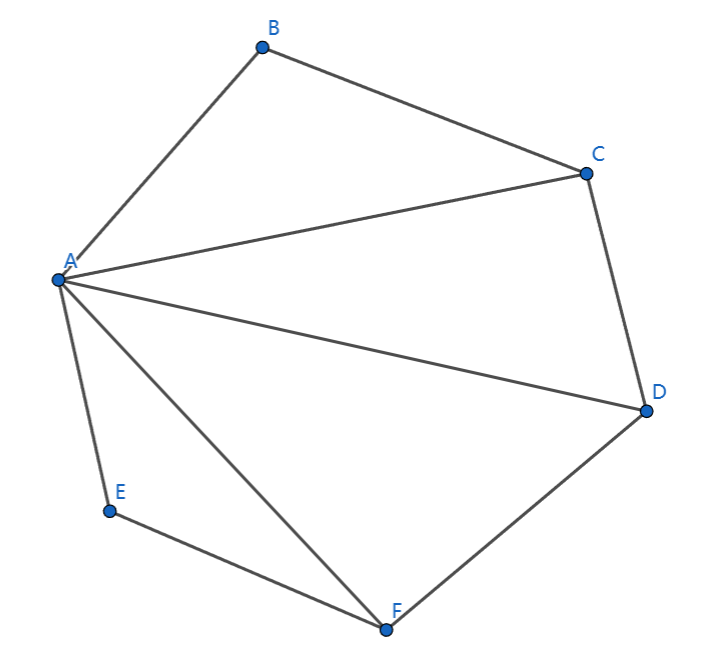
这样剖分可以实现求面积,但是有点不太通用
还有另外一种比较简单的
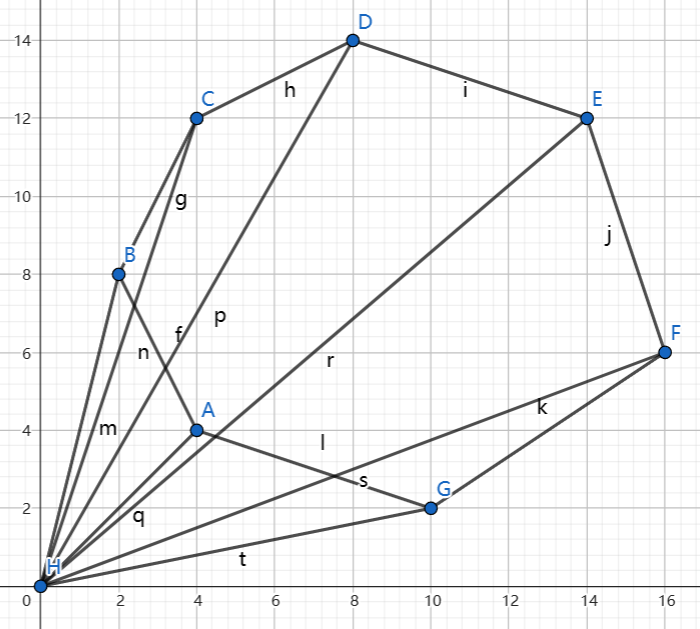
减去ABH和AHG的面积,再加上剩下的三角形的面积,发现正好绕这个凸多边形转一圈,相邻点与原点形成的向量两两求叉积再相加就行了,自己带着正负,最后取绝对值即可
然后,发现这玩意好像对非凸多边形也适用
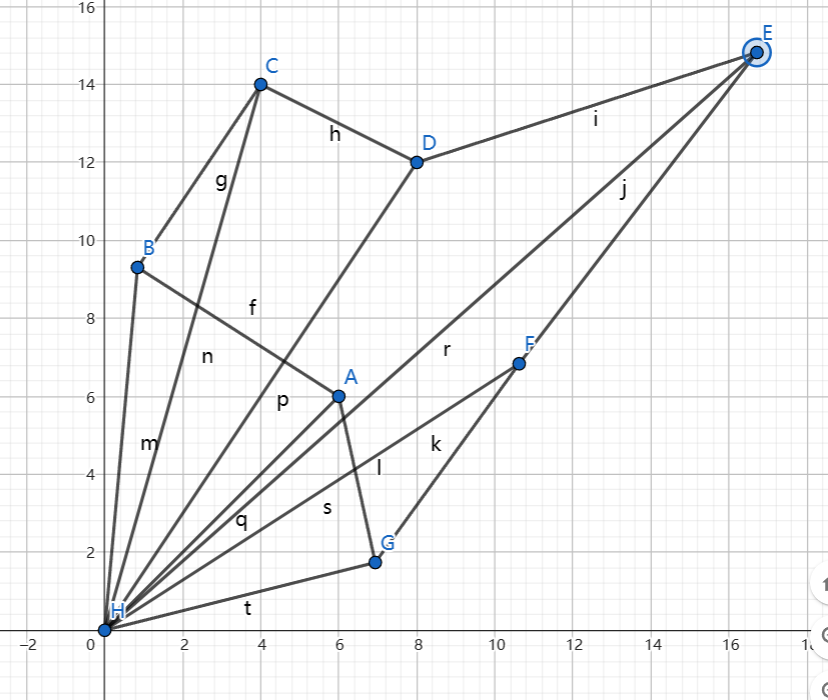
也可以直接按照点的顺序,绕一圈回来即可,但是一般来说,我们比较常用的是凸多边形的面积求解
凸包
定义不再细说,就是用周长最短的凸多边形把几个点框起来
这里只讲一种比较常用的求解凸包的做法,上下凸包分开求
离线的话,可以先按照横坐标排序,使用队列或者栈,一个一个从左往右往队列中加,加的时候判断一下这个点和队尾的点形成的向量与这个点和次尾的点形成的向量的关系,决定一下是不是要把队尾弹出
这样的过程
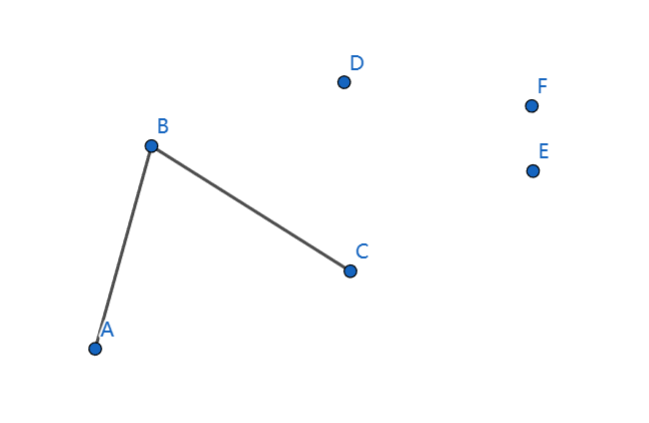
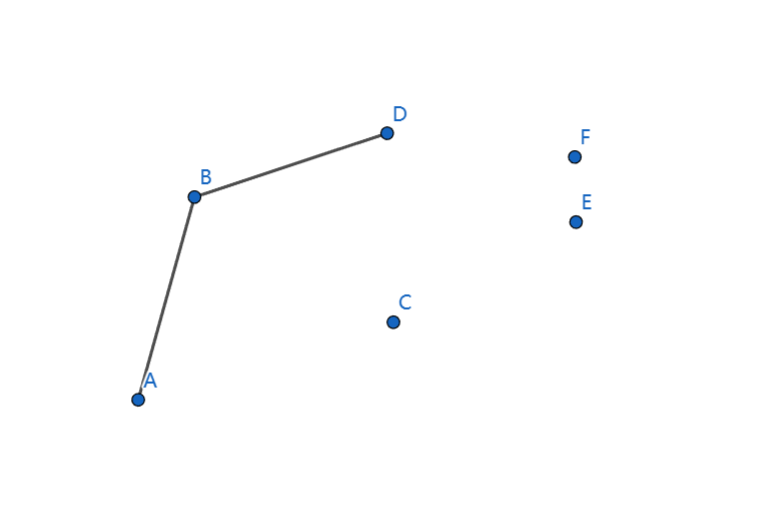
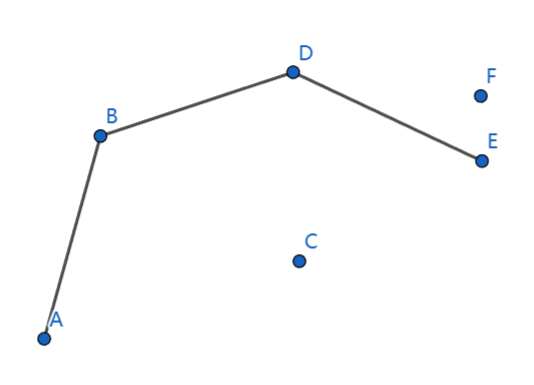
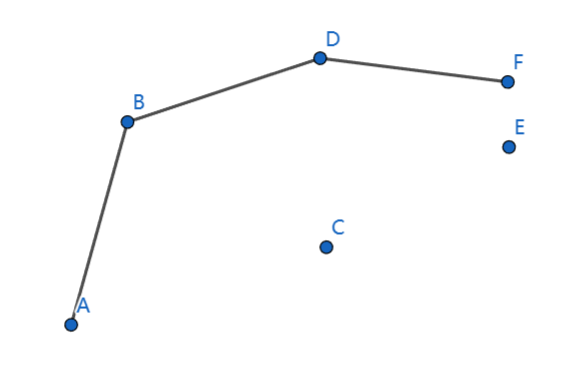
这个过程是上凸包,下凸包是一样的过程,最后两个凸包怼到一起就行了,注意下凸包要从右到左横坐标排序
在线做法和离线做法很相似,用set插入删除即可,前面后面都删一删就行了,常数比较大
code
struct node{
int x,y;
bool operator < (node a)const{return x<a.x;}
bool operator == (node a)const{return a.x==x&&a.y==y;}
};
double K(node a,node b){return 1.0*(b.y-a.y)/(b.x-a.x);}
bool comp(node a,node b,node c){return K(a,b)<=K(b,c);}
double D(node a,node b){double xx=a.x-b.x,yy=a.y-b.y;return sqrt(xx*xx+yy*yy);}
set<node> st;
double sum;
void erase(set<node>::iterator it){
set<node>::iterator i=next(it),j=prev(it);
sum-=D(*j,*it);sum-=D(*it,*i);sum+=D(*j,*i);
st.erase(it);
}
void ins(node a){
set<node>::iterator it=st.lower_bound(a);
if(it!=st.end()&&it->x==a.x){
if(it->y<=a.y)erase(it);
else return ;
}
while(true){
set<node>::iterator i=st.lower_bound(a);
if(i==st.begin())break;
i--;if(i==st.begin())break;
set<node>::iterator j=prev(i);
if(comp(*j,*i,a))erase(i);
else break;
}
while(true){
set<node>::iterator i=st.lower_bound(a);
if(i==st.end())break;
set<node>::iterator j=next(i);
if(j==st.end())break;
if(comp(a,*i,*j))erase(i);
else break;
}
it=st.lower_bound(a);
if(it==st.begin()){sum+=D(a,*it);st.insert(a);}
else if(it==st.end()){sum+=D(*prev(it),a);st.insert(a);}
else {
set<node>::iterator i=prev(it);
if(!comp(*i,a,*it)){
sum-=D(*i,*it);
sum+=D(*i,a);sum+=D(a,*it);
st.insert(a);
}
}
}
半平面交
半平面就是指一条直线的一侧的所有点构成的集合,半平面可以用向量来表示,向量所在直线就是割开平面的线,一般表示向量左侧的半平面
半平面交,字面意思,就是一堆半平面,一堆点的集合,这些集合求交,实际上就是所有半平面都包含的区域,我们就是要求解这一块区域,S&I算法
首先是极角排序,C++库函数中有一个\(atan2(y,x)\),可以直接计算一条直线的倾斜角,\(\theta=arctan\frac{y}{x}\),用它排序的话,就可以直接规范直线的方向了
如果排序的时候遇到平行向量,因为我们要用的是左半平面,所以平行向量用左边的就行了,判断左侧的时候,用用两个向量的起点相连,乘上另外一个向量,通过正负就能判断了
排完序之后,就使用一个队列,求交即可
求交的过程类似凸包,无用的向量可以删掉,手画一个....
注意用队列的时候,前后都得去检验一下,要不然求出来有可能是不对的,在快结束的时候,有可能会把队首的也排掉....继续手画
代码在这里
#include<bits/stdc++.h>
using namespace std;
#define fo(i,x,y) for(int i=(x);i<=(y);i++)
#define fu(i,x,y) for(int i=(x);i>=(y);i--)
int read(){
int s=0,t=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')t=-1;ch=getchar();}
while(isdigit(ch)){s=(s<<1)+(s<<3)+(ch^48);ch=getchar();}
return s*t;
}
const int N=1005;
struct VEC{
double x,y;
VEC(){}VEC(double a,double b){x=a;y=b;}
void rad(){x=read();y=read();}
VEC operator + (VEC a)const{return VEC(x+a.x,y+a.y);}
VEC operator - (VEC a)const{return VEC(x-a.x,y-a.y);}
VEC operator * (double a)const{return VEC(x*a,y*a);}
VEC operator / (double a)const{return VEC(x/a,y/a);}
double operator * (VEC a)const{return x*a.x+y*a.y;}
double operator ^ (VEC a)const{return x*a.y-y*a.x;}
};
struct LNE{
VEC o,v;double ang;
LNE(){}LNE(VEC a,VEC b){o=a;v=b;ang=atan2(v.y,v.x);}
}q[N],l[N];
VEC cro(LNE a,LNE b){return b.o+b.v*(((b.o-a.o)^a.v)/(a.v^b.v));}
bool left(LNE a,LNE b){return (a.v^(b.o-a.o))<0;}
bool com(LNE a,LNE b){
if(a.ang!=b.ang)return a.ang<b.ang;
return left(a,b);
}
bool jud(LNE a,LNE ltp,LNE top){
return (a.v^(cro(ltp,top)-a.o))<0;
}
int ql,qr,cnt;
double ans;
signed main(){
int n=read();
while(n--){
int m=read()-1;VEC fi,se,on;
fi.rad();on=fi;
while(m--){
se.rad();
l[++cnt]=LNE(fi,se-fi);
fi=se;
}
l[++cnt]=LNE(fi,on-fi);
}
sort(l+1,l+cnt+1,com);
ql=1;qr=0;
fo(i,1,cnt)if(l[i].ang!=l[i-1].ang){
while(ql<qr&&jud(l[i],q[qr-1],q[qr]))qr--;
while(ql<qr&&jud(l[i],q[ql],q[ql+1]))ql++;
q[++qr]=l[i];
}
while(ql<qr&&jud(q[ql],q[qr-1],q[qr]))qr--;
// while(ql<qr&&jud(q[qr],q[ql],q[ql+1]))ql++;
VEC beg=cro(q[ql],q[ql+1]);
fo(i,ql+1,qr-2)ans+=((cro(q[i],q[i+1])-beg)^(cro(q[i+1],q[i+2])-beg))/2;
ans+=((cro(q[qr-1],q[qr])-beg)^(cro(q[qr],q[ql])-beg))/2;
printf("%.3lf",ans);
}


