noip模拟49[不是为啥这么难啊]
noip模拟49 solutions
开学之后的第一次考试,一考就完蛋
65pts,心态炸了
时间分配这方面还是可以的,就是脑子不太听话,
所以以后要调整好状态再考
T1 Reverse
不过说实话这个题真的眼熟,一眼就是最短路,
然后看了看时间复杂度,好像不太对
dijkstra的复杂度里好像有一个m,
这里重申一下堆优化的dijkstra的时间复杂度是\(\mathcal{O(m+nlogn)}\)
所以这个题的边数最大是\(n^2\)所以你不炸谁炸
我们要找到一个去重的办法把走过的都删去
有很多种,可以用set,也可以用链表,前者是\(\mathcal{O(nlogn)}\),后者是\(\mathcal{O(n)}\)
因为懒所以直接用的set
AC_code
#include<bits/stdc++.h>
using namespace std;
#define re register int
const int N=1e5+5;
int n,k,m,s;
bool fl[N];
set<int> st[2];
queue<int> q;
int ans[N];
signed main(){
scanf("%d%d%d%d",&n,&k,&m,&s);
for(re i=1,x;i<=m;i++)scanf("%d",&x),fl[x]=true;
for(re i=1;i<=n;i++)if(i!=s&&!fl[i])st[i&1].insert(i);
memset(ans,-1,sizeof(ans));
q.push(s);ans[s]=0;
while(!q.empty()){
int x=q.front();q.pop();
//cout<<x<<endl;
int l=max((k>>1)-(x-(k+1>>1))+1,x-k+1);
int r=min((n-(k+1>>1))+(n-(k>>1)-x)+1,x+k-1);
int f=((k^1)&1)^(x&1);
set<int>::iterator it=st[f].lower_bound(l);
//int f=((k^1)&1)&(x&1);
while(*it>=l&&*it<=r&&it!=st[f].end()){
//cout<<*it<<endl;
q.push(*it);
ans[*it]=ans[x]+1;
st[f].erase(it);
it=st[f].lower_bound(l);
}
}
for(re i=1;i<=n;i++)printf("%d ",ans[i]);
}
T2 Silhouette
主要是观察,我倒是能想出来排序重组之后方案数是不变的
也能想到每一个格子都有一个最大值的限制
考场上也一直在想要如何把这个每一行和每一列必须含有一个最大值的限制给解决掉了
我一直在想容斥,想要分别容斥行和列的情况,最后再合并
但是我发现这样根本就做不出来,然后就弃掉了
看完题解后发现,我可以在计算方案数的时候保证列是全部合法的
然后去容斥出来行的情况
于是我们就得到了题解上那个计算矩形的式子的拓展形式,就是也可以计算L型的,
我们先设变量,然后直接把式子放在下面,挺好理解的,自己推一推
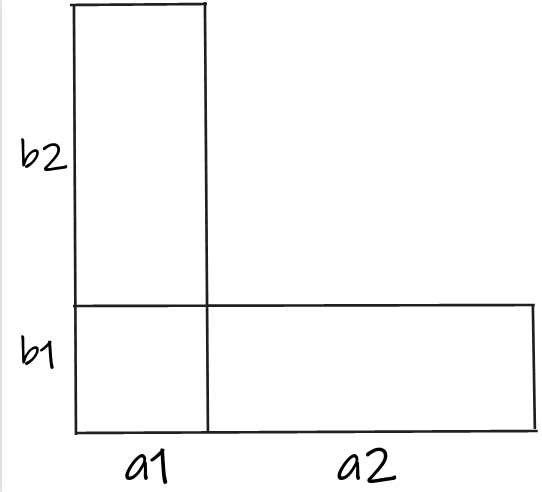
当前的L型内最大取值为s
AC_code
#include<bits/stdc++.h>
using namespace std;
#define re register int
const int N=1e5+5;
const int mod=1e9+7;
int n,a[N],b[N],c[N*2],cc,f[N],ans=1,jc[N];
int ksm(int x,int y){int ret=1;while(y){if(y&1)ret=1ll*ret*x%mod;x=1ll*x*x%mod;y>>=1;}return ret;}
int C(int x,int y){return 1ll*jc[x]*ksm(1ll*jc[y]*jc[x-y]%mod,mod-2)%mod;}
signed main(){
scanf("%d",&n);jc[0]=1;
for(re i=1;i<=n;i++)jc[i]=1ll*jc[i-1]*i%mod;
for(re i=1;i<=n;i++)scanf("%d",&a[i]),c[++cc]=a[i];
for(re i=1;i<=n;i++)scanf("%d",&b[i]),c[++cc]=b[i];
sort(a+1,a+n+1);sort(b+1,b+n+1);sort(c+1,c+cc+1);
cc=unique(c+1,c+cc+1)-c-1;
if(a[n]!=b[n]){printf("0");return 0;}
int ia=0,ib=0,ca,da,cb,db;
for(re i=1;i<=cc;i++){
ca=da=cb=db=0;
while(a[ia+1]<=c[i]&&ia+1<=n){ia++;if(a[ia]==c[i])ca++;}
while(b[ib+1]<=c[i]&&ib+1<=n){ib++;if(b[ib]==c[i])cb++;}
if(cb)da=n-ia;if(ca)db=n-ib;
for(re j=0;j<=ca;j++)f[j]=1ll*C(ca,j)*(1ll*ksm(1ll*ksm(c[i],j)*((1ll*ksm(c[i]+1,ca+da-j)+mod-ksm(c[i],ca+da-j))%mod)%mod,cb)*ksm(1ll*ksm(c[i],j)*ksm(c[i]+1,ca-j)%mod,db)%mod)%mod;
int xs=1,res=0;
for(re j=0;j<=ca;j++)res=(1ll*res+mod+xs*f[j]%mod)%mod,xs=-xs;
ans=1ll*ans*res%mod;
}
printf("%d",ans);
}
T3 Seat
显然这个题我不会,所以直接std了,难难难难难难难难难难
所以我思路半懂不懂吧,反正要让我考场上想到,不可能的
主要是两个结论,也就是题解上的那个、
对于任意一个人,他坐下时离最近的人的距离是固定的,不随前面的人的决策而改变。这样我们可以将所有人按坐下时的距离分成若干层
无论之前每一层如何决策,轮到这一层时逬空区间的长度构成的可重集也是固定的。
这两个结论也就告诉你,你可以通过其中一种情况知道其他所有情况的信息
那么我们只需要通过这一种情况来推得全部的概率
当然还有另外一个事情,在偶数长度的区间中,我们会有两种选择
考场上的时候我觉得这个完全处理不了
但是题解一句话点醒了我,
两种情况是完全对称的
所以我们也只需要选择一种,算出来所有的概率之后,再平均分给这两种对称的情况
所以代码细节十分的多。
总体思路:我们先找到其中一种合法的情况,也就找到了每一层的可选区间个数和偶数个数
然后我们根据这些信息来dp,dp[i][j]表示某一层选了i个,还剩下j个偶数长度的区间
dp完之后,我们对于每个偶数区间都做一下对称性的拆分,就是除以2
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define re register int
const int N=3e3+5;
int n,sum,mod,f[N][N],g[N][N],ans[N][N],pos[N],odd[N],cnt[N],inv[N];
bool vis[N];
signed main(){
scanf("%lld%lld",&n,&mod);sum=n;
vis[0]=vis[n+1]=true;
for(re i=1;i<=n;i++){
int ql=0,qr=0,mx;
for(re j=0;j<=n;j++){
int r=j+1;
while(!vis[r])r++;
if(r-j>qr-ql)ql=j,qr=r;
j=r-1;
}
mx=qr-ql>>1;vis[ql+mx]=true;
cnt[mx]++;odd[mx]+=(qr-ql)&1;
pos[i]=ql+mx;
}
inv[1]=1;for(re i=2;i<=n;i++)inv[i]=mod-mod/i*inv[mod%i]%mod;//cout<<inv[i]<<endl;
for(re i=1;i<=n;i++){
if(!cnt[i])continue;
int l=sum-cnt[i]+1,r=sum;
if(i==1){
for(re j=l;j<=r;j++)
for(re k=l;k<=r;k++)
ans[j][pos[k]]=inv[cnt[i]];
sum-=cnt[i];
continue;
}
for(re j=0;j<=cnt[i];j++)
for(re k=0;k<=odd[i];k++)
f[j][k]=0;
f[0][odd[i]]=1;
int p=l+odd[i]-1;
for(re j=1;j<=cnt[i];j++){
int oddw=0,evew=0;
for(re k=0;k<=odd[i];k++){
if(!f[j-1][k])continue;
int mu=cnt[i]-j+1+k;
if(k){
int tmp=f[j-1][k]*k*2%mod*inv[mu]%mod;
f[j][k-1]=(f[j][k-1]+tmp)%mod;
oddw=(oddw+tmp*inv[odd[i]*2])%mod;
}
if(cnt[i]-odd[i]){
int tmp=f[j-1][k]*(mu-2*k)%mod*inv[mu]%mod;
f[j][k]=(f[j][k]+tmp)%mod;
evew=(evew+tmp*inv[cnt[i]-odd[i]])%mod;
}
}
for(re k=l;k<=p;k++){
ans[l+j-1][pos[k]]=(ans[l+j-1][pos[k]]+oddw)%mod;
ans[l+j-1][pos[k]+1]=(ans[l+j-1][pos[k]+1]+oddw)%mod;
}
for(re k=p+1;k<=r;k++)ans[l+j-1][pos[k]]=(ans[l+j-1][pos[k]]+evew)%mod;
}
for(re j=l;j<=p;j++){
int ql=pos[j]-i+1,qr=pos[j]+i;
for(re k=ql;k<=qr;k++){
if(k==pos[j])continue;
for(re s=r+1;s<=n;s++){
int dc=k<pos[j]?k+i+1:k-i;
int tmp=ans[s][k]*inv[2]%mod;
g[s][k]=(g[s][k]+tmp)%mod;g[s][dc]=(g[s][dc]+tmp)%mod;
}
}
for(re s=r+1;s<=n;s++)
for(re k=ql;k<=qr;k++)
ans[s][k]=g[s][k],g[s][k]=0;
}
sum-=cnt[i];
}
for(re i=1;i<=n;i++){
for(re j=1;j<=n;j++)
printf("%lld ",ans[i][j]);
printf("\n");
}
}


