noip模拟45[真是啥也不会]
noip模拟45 solutions
真是一个题都不会了，然而考完试之后我在10min之内切掉了最后一个题
话说这是为什么呢，
因为最后一个是回滚莫队的大板子，然而我忘记了，不不不，是没有记起来过
T1 打表
好像还真的是一个打表题，找找规律就能过，真的
结论就是
\(\huge res=\frac{\sum\limits^{n}_{i=1}abs(x_i-x_{ans})}{2^k}\)
这个是可以证出来的，
首先对于只剩下一位没有选的时候，肯定是一个CPU选1，另外一个选0
我们考虑剩下更多的情况，可以知道每次两个CPU都会选择同一位进行操作，并选择不同的数
所以期望仍然是一半一半，所以还是剩下的数的差的平均数
AC_code
#include<bits/stdc++.h>
using namespace std;
#define re register int
#define ll long long
const int N=1<<18;
const ll mod=1e9+7;
ll k,ans,a[N],res;
ll ksm(ll x,ll y){
ll ret=1;
while(y){
if(y&1)ret=ret*x%mod;
x=x*x%mod;
y>>=1;
}
return ret;
}
signed main(){
scanf("%lld%lld",&k,&ans);
for(re i=0;i<(1<<k);i++)scanf("%lld",&a[i]);
ans=a[ans];
for(re i=0;i<(1<<k);i++)res=(res+abs(a[i]-ans))%mod;
printf("%lld",res*ksm(ksm(2ll,k),mod-2)%mod);
}
其实考场上没有看懂题，还找人讲了一下
T2 蛇
好象是CF的原题，我也没做过，暴搜还打错了，不知道为啥，不打了，直接正解
肯定是扭来扭去的走的，最后接上两个平着的
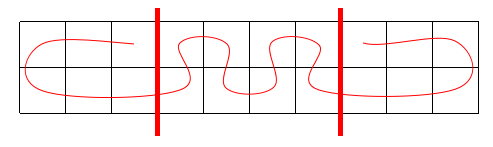
那我们就设dp[i][j][k][0/1]表示在第i行，第j列，匹配到了第k个字符
0表示可以竖着转移，1表示不可以
我们直接枚举下一个字符，转移就行了
前面的那个横着的直接预处理就好了，后面的等到dp完了之后再处理
这个处理就用hash就行了
AC_code
#include<bits/stdc++.h>
using namespace std;
#define re register int
#define ull unsigned long long
#define ll long long
const ull bas=131;
const int N=2005;
const ll mod=1e9+7;
ll n,m,dp[2][N][N][2],ans;
char ch[2][N],a[N];
ull hc[2][2][N],ha[N],ba[N];
ull get_hc0(int x,int l,int r){return hc[x][0][r]-hc[x][0][l-1]*ba[r-l+1];}
ull get_hc1(int x,int l,int r){return hc[x][1][l]-hc[x][1][r+1]*ba[r-l+1];}
ull get_ha(int l,int r){return ha[r]-ha[l-1]*ba[r-l+1];}
void get_ans(){
memset(dp,0,sizeof(dp));
for(re i=0;i<=1;i++)for(re j=1;j<=n;j++)hc[i][0][j]=hc[i][0][j-1]*bas+ch[i][j]-'a';
for(re i=0;i<=1;i++)for(re j=n;j>=1;j--)hc[i][1][j]=hc[i][1][j+1]*bas+ch[i][j]-'a';
for(re i=0;i<=1;i++)for(re j=1;j<=n;j++){
dp[i][j][1][0]=(ch[i][j]==a[1]);
for(re k=2;k<=j;k++)
if((k<<1)<=m)dp[i][j][k<<1][1]=(get_hc0(i,j-k+1,j)==get_ha(k+1,k<<1)&&get_hc1(i^1,j-k+1,j)==get_ha(1,k));
}
for(re k=1;k<=m;k++)for(re i=0;i<=1;i++)for(re j=1;j<=n;j++){
if(ch[i][j]!=a[k])continue;
dp[i][j][k][0]=(dp[i][j][k][0]+dp[i][j-1][k-1][0]+dp[i][j-1][k-1][1])%mod;
dp[i][j][k][1]=(dp[i][j][k][1]+dp[i^1][j][k-1][0])%mod;
}
for(re i=0;i<=1;i++)for(re j=1;j<=n;j++)for(re k=0;k<=m;k++){
if((m-k)&1)continue;
if(m-k==2)continue;
int mid=m-k>>1;
if(m!=k&&(j+mid>n||get_hc0(i,j+1,j+mid)!=get_ha(k+1,k+mid)||get_hc1(i^1,j+1,j+mid)!=get_ha(k+mid+1,m)))continue;
ans=(ans+dp[i][j][k][0]+dp[i][j][k][1])%mod;
}
}
signed main(){
scanf("%s",ch[0]+1);scanf("%s",ch[1]+1);n=strlen(ch[0]+1);
scanf("%s",a+1);m=strlen(a+1);ba[0]=1;
for(re i=1;i<=m;i++)ba[i]=ba[i-1]*bas,ha[i]=ha[i-1]*bas+a[i]-'a';
get_ans();
reverse(ch[0]+1,ch[0]+n+1);
reverse(ch[1]+1,ch[1]+n+1);
get_ans();
if(m==1)for(re i=0;i<=1;i++)for(re j=1;j<=n;j++)ans=(ans-(ch[i][j]==a[1])+mod)%mod;
if(m==2)for(re i=0;i<=1;i++)for(re j=1;j<=n;j++)ans=(ans+mod-(ch[i][j]==a[1]&&ch[i^1][j]==a[2]))%mod;
printf("%lld",ans);
}
T3 购物
这个说白了也是一个结论题，我还是不会
结论：我们在K的覆盖轴上，可能出现空缺的点一定在i-1的前缀和与\(\frac{x_i}{2}\)之间
我们证明这个结论：
我们现在不在乎i-1之前如何，我们之在乎i这个数，
设\(sum_i\)为前i个数的和，\(x_i\)为第i个数，我们按照\(x_i\)从小到大排序
如果在\(sum_{i-1}\)和\(\frac{x_i}{2}\)之间出现了没有覆盖的点，
因为后面的点都比\(x_i\)大，所以没有点可以填补这个空缺
还要证明\(\frac{x_i}{2}-sum_i\)这个区间是连续的
首先\(sum_i=sum_{i-1}+x_i\)那么\(\frac{sum_i}{2}\le\max(x_i,sum_{i-1})\)
所以这样的区间一定可以接上。
AC_code
#include<bits/stdc++.h>
using namespace std;
#define re register int
#define ll long long
const int N=1e5+5;
ll n,a[N],sum[N],rec;
signed main(){
scanf("%lld",&n);
for(re i=1;i<=n;i++)scanf("%lld",&a[i]);
sort(a+1,a+n+1);
for(re i=1;i<=n;i++){
rec+=((a[i]+1)/2-sum[i-1]-1>0?(a[i]+1)/2-sum[i-1]-1:0);
sum[i]=sum[i-1]+a[i];
}
printf("%lld",sum[n]-rec);
}
T4 ants
题面翻译：给定l,r，求[l,r]区间内的数的最长连续段
回滚莫队大板子。。。
AC_code
#include<bits/stdc++.h>
using namespace std;
#define re register int
const int N=100005;
int n,m;
int c[N],pos[N],di;
int ans[N];
int lb[N],rb[N];
struct query{
int l,r,id,p;
}qus[N];
struct front{
int typ,p,val;
}fro[N];
inline bool comp(query x,query y){
if(pos[x.l]==pos[y.l])
return x.r<y.r;
return x.l<y.l;
}
int main(){
scanf("%d%d",&n,&m);
di=sqrt(n);
for(re i=1;i<=n;i++){
scanf("%d",&c[i]);
pos[i]=i/di+1;
}
for(re i=1;i<=m;i++){
scanf("%d%d",&qus[i].l,&qus[i].r);
qus[i].id=i;
qus[i].p=pos[qus[i].l];
}
sort(qus+1,qus+m+1,comp);
int r,sum,res,tmp;
for(re i=1;i<=m;i++){
if(qus[i].p!=qus[i-1].p){
sum=0;
for(re j=1;j<=n;j++)
lb[j]=rb[j]=0;
r=qus[i].p*di;
}
while(r<qus[i].r){
r++;
lb[c[r]]=lb[c[r]-1]+1;
rb[c[r]]=rb[c[r]+1]+1;
tmp=lb[c[r]]+rb[c[r]]-1;
sum=max(sum,tmp);
lb[c[r]+rb[c[r]]-1]=tmp;
rb[c[r]-lb[c[r]]+1]=tmp;
}
res=sum;
int s=0;
for(re l=qus[i].l;l<=min(qus[i].r,qus[i].p*di);l++){
lb[c[l]]=lb[c[l]-1]+1;
rb[c[l]]=rb[c[l]+1]+1;
tmp=lb[c[l]]+rb[c[l]]-1;
res=max(res,tmp);
fro[++s].typ=1;fro[s].p=c[l]+rb[c[l]]-1;fro[s].val=lb[c[l]+rb[c[l]]-1];
fro[++s].typ=2;fro[s].p=c[l]-lb[c[l]]+1;fro[s].val=rb[c[l]-lb[c[l]]+1];
lb[c[l]+rb[c[l]]-1]=tmp;
rb[c[l]-lb[c[l]]+1]=tmp;
}
ans[qus[i].id]=res;
for(re j=s;j>=1;j--){
if(fro[j].typ==1)
lb[fro[j].p]=fro[j].val;
else
rb[fro[j].p]=fro[j].val;
}
for(re j=qus[i].l;j<=min(qus[i].r,qus[i].p*di);j++){
lb[c[j]]=rb[c[j]]=0;
}
}
for(re i=1;i<=m;i++){
printf("%d\n",ans[i]);
}
}
QQ:2953174821
