hall定理(霍尔定理)略解

扯淡

原名好像是叫hall婚姻定理，好象是用来配对的

然后现在被用来做二分图了

确实非常的好用，这里主要记一下定理的意义极其证明

方便复习

匹配

所谓二分图匹配，就是在二分图上找到一个没有交点的边集

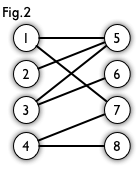
（图片转载自这里

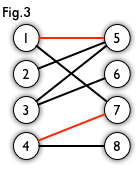
图3表示的就是一个二分图匹配

但是此时3与6的边也可以加入现在的边集

所以此时的匹配不是最大匹配，可是即使加上了也不是最大匹配

最大匹配的定义就是，能够覆盖的点集的大小最大

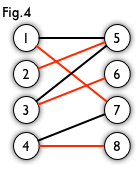
那图4就是最大匹配了，因为他是可以覆盖点集最大的边集，也就是边最多的边集

当然，此时这个匹配也是这个二分图的完美匹配

完美匹配的定义就是，能够覆盖所有的点的匹配

完美匹配：设 M 是二分图 G(V1,V2,E)(|V1|≤|V2|) 的一个匹配，若 ∀vi∈V1,∃k∈V2,(vi,k)∈M，则称 M 为 G 的一个完美匹配。

所以，完美匹配一定是最大匹配，但是最大匹配不一定是完美匹配

好像求二分图匹配的有一个叫做'匈牙利算法',但是我不会

hall 定理

显然

我真的觉得挺显然的，你既然要找到二分图的完美匹配

就要找到一个边集覆盖所有的点而且不能有交点，

边还只能连接两侧，所以，

二分图存在完美匹配的一个条件就是两侧点集大小相同

这很显然吧

定理内容

第二个条件就可以用hall定理来解释了

Hall 定理：对于一个二分图 \(G(V1,V2,E)(|V1|≤|V2|)\)，
对于\(∀X⊆V1\)，定义 \(N(X)={vj|(vi,vj)∈E,vj∈V2,vi∈X}\)。
其存在 \(V1\) 的完美匹配的充要条件为 \(∀X⊆V1,|X|≤|N(X)|\)。

简单来说，就是对于二分图其中一个点集的子集
向另外一个点集连边，任意这样的子集所能连到的对应的节点集合大小大于当前集合

证明

必要性的话，显然吧，如果连边比当前点集小的话，那就不够了，一定会有剩下的点，

充分性可以通过网络流的思想来证明

如果当前二分图满足hall定理，但是没有找到一个完美匹配

那么两侧分别会剩下一些点，此时我们拿出一个点来

这样的话，这个点一定会有一条连边连向对面，如果对面的点没有选那就直接选上

如果被选了，那也选上，然后它之前连的点就会剩下，那么我再次进行这个过程

然后就会出现一条增广路，最后找到完美匹配。。。

口胡证明，