noip模拟6[辣鸡·模板·大佬·宝藏]
这怕不是学长出的题吧
这题就很迷
这第一题吧,正解竟然是O(n2)的,我这是快气死了,考场上一直觉得aaaaa n2过不了过不了,
我就去枚举边了,然后调了两个小时,愣是没调出来,然后交了个暴力,就走了15pts
然后我就淦第二题,这第一眼扫过去,就觉得是树链剖分,然后连复杂度都没算,就生生的码了一个小时,
给我弄傻了,好像复杂度是(8n+?????nlogn)的,然后看了看最坏是(n2logn)的,不卡死你才怪!!!
然后这第三题吧,是这场考试中最让我后悔的一道题,看到概率期望就害怕,然后最后去干他,然后就没打完,然后还没思路
但是我总结到一个经验
有关有规律的随机数的问题,完全不需要考虑什么后效性,因为,是随机的,情况多去了
第四题,这是个非常非常狗的题,狗不狗先放一边,问题是他竟然是 李煜东蓝书上的原题,我没看到,但有人看过了。哇呜呜
还有一个事,这是我第一次在考场上用到对拍程序,还是有点小小的成就感的;
然后就是正解啦,这次改题非常顺利,没有浪费一丁点的时间
T1辣鸡
题目大意:给你张图,上面有好多为1的点,求这些点中,能够相邻并且利用对角线相连的边
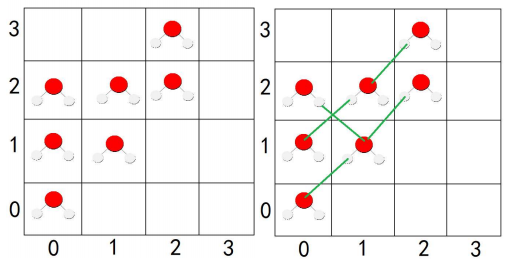 就这样连接
就这样连接
然后这些点是通过一个一个小矩形给出来的,每次给出左下角和右上角的坐标,然后就可以计算了
第一眼看到这个题,我就直接蒙了一会,因为题面给了一个“曼哈顿距离”,就把我弄傻了
然后就打了个枚举点的极其暴力的打法,验证了我的猜想是正确的
然后我就开始想正解,显然我意识到了先算自己矩形内部的连边,再算两两矩形之间的连边
然后我想到了可以一个矩形一个矩形的枚举,然而,我在两秒钟之后就否掉了这个想法,因为,我认为复杂度太高了
可是苍天不公,这竟然是正解!!!!
首先枚举每个矩形内部的连边,O(1)计算 (y2-y1)*(x2-x1);
在枚举矩形之间的连边之前要先排序,按照x1升序,y1升序,排列
然后再枚举,注意这时候的各种判断就来了
自己推吧,主要注意判断两个矩形对角的时候,这个要单独判断,而且,不能与其他情况混起来算
然后先i-n j=i+1~~n这样枚举,可以有减支的机会,如果向前枚举,那么只能不断continue,而不能break
这样时间就足以满足AC这道题了!!~~~
然后贴上代码,代码没有注释,自己看思路,然后理解代码,能不看就别就看

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define int long long 4 #define re register int 5 const int N=100005; 6 struct node{ 7 int xa,xb,ya,yb; 8 int zs,zx,ys,yx; 9 }pos[N]; 10 int n,ans; 11 bool com(node a,node b){ 12 if(a.xa==b.xa)return a.ya<b.ya; 13 return a.xa<b.xa; 14 } 15 signed main(){ 16 scanf("%lld",&n); 17 for(re i=1;i<=n;i++){ 18 scanf("%lld%lld%lld%lld",&pos[i].xa,&pos[i].ya,&pos[i].xb,&pos[i].yb); 19 } 20 sort(pos+1,pos+n+1,com); 21 for(re i=1;i<=n;i++){ 22 ans+=2*(pos[i].xb-pos[i].xa)*(pos[i].yb-pos[i].ya); 23 for(re j=i+1;j<=n;j++){ 24 if(pos[j].xa-1>pos[i].xb)break; 25 if(pos[i].ya-1>pos[j].yb)continue; 26 if(pos[j].ya-1>pos[i].yb)continue; 27 if(pos[j].xa-1==pos[i].xb&&(pos[i].ya-1==pos[j].yb||pos[j].ya-1==pos[i].yb)){ 28 ans++; 29 continue; 30 } 31 if(pos[j].xa-1==pos[i].xb){ 32 ans+=2*(min(pos[i].yb,pos[j].yb)-max(pos[i].ya,pos[j].ya)); 33 if(pos[i].ya!=pos[j].ya)ans++; 34 if(pos[i].yb!=pos[j].yb)ans++; 35 continue; 36 } 37 if(pos[j].ya-1==pos[i].yb||pos[i].ya-1==pos[j].yb){ 38 ans+=2*(min(pos[i].xb,pos[j].xb)-max(pos[i].xa,pos[j].xa)); 39 if(pos[i].xa!=pos[j].xa)ans++; 40 if(pos[i].xb!=pos[j].xb)ans++; 41 continue; 42 } 43 } 44 } 45 printf("%lld",ans); 46 }
T2模板
题目大意:给你一棵树,每次任选一个节点,将这个节点到根的路径上都添加一个颜色,当然,每个点最多添加k[i]个颜色,最后让你统计,每个点的颜色种类数
我第一眼:卧槽!!
我第二眼:这不是链!!??
我第三眼:剖分!!没的商量
然后我就风风火火的码了一个小时的树链剖分,然后信心满满的期待着满分,等来的却是0
对!他竟然管这题叫模板!!!怎么敢的
其实这个题的正解是线段树的启发式合并,其实也算是广义的线段树合并,因为他并没有直接去合并两颗线段树
而是不断的向其中一棵树插入另一棵树的节点,然后统计信息,因为这个题要统计的东西有点麻烦
既然每次向某一个节点插入颜色,那我们就先向这个节点插入,那么就“启发”你要向上合并了
好像我还想到了一点点正解,因为我读代码的时候不知道为什么要找到这个点的重儿子
后来才明白,因为这样的话可以尽量省去时间复杂度(这里的重儿子不是子树大小最大,而是子树中添加的颜色最多)时间就被省去好多
然后还要动态开点,因为这个空间复杂度实在是太高了,而且,对于每一次加颜色来说,只用到了线段树上的一条链,空间也大大优化了
还有就是统计颜色种类的问题
我们按照时间去建立一颗线段树,然后每个节点都要存放两个变量,颜色种类和所有颜色的数量
这样就符合了线段树的建立要求没可以进行上下转移,可以优化时间
同种颜色我们只能统计一次,按照常人的思路,都会去统计每种颜色第一次出现的时间,当然你要去统计最后一次也没人管你,就改个符号就好了
不对不对统计最后一次是不可以的,因为我们可以加的颜色数量是有限的,所以要统计第一次
然后每次合并的时候都把这个颜色的首次出现的时间更新;
这时候就和普通的线段树合并有不一样的了
普通的线段树合并,只是简单的将两颗子树的信息合并在一起,没有办法更新这颗树上原来最早的这个颜色的权值
所以我们带着要合并到的那个根去遍历另外一颗树,然后到了叶子节点,如果叶子节点存在,那就向我们带着的那个根中插入
在插入的过程中更新某种颜色的第一次出现的位置
这样就可以想普通线段树一样查询答案了;
代码(无注释)

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define re register int 4 const int N=100005; 5 int n,m; 6 int to[N*2],nxt[N*2],head[N],rp; 7 int k[N]; 8 struct node{ 9 int x,c; 10 }dem[N]; 11 int lsh[N],lh; 12 void add_edg(int x,int y){ 13 to[++rp]=y; 14 nxt[rp]=head[x]; 15 head[x]=rp; 16 } 17 vector<int> mp[N]; 18 int rt[N]; 19 struct noda{ 20 int num[N*80],kin[N*80]; 21 int ls[N*80],rs[N*80]; 22 int seg; 23 int pre[N],fro[N],tot; 24 void pushup(int x){ 25 num[x]=num[ls[x]]+num[rs[x]]; 26 kin[x]=kin[ls[x]]+kin[rs[x]]; 27 } 28 void ins(int &x,int l,int r,int pos,int ki,int nu){ 29 if(!x)x=++seg; 30 if(l==r){ 31 kin[x]=ki; 32 num[x]=nu; 33 return ; 34 } 35 int mid=l+r>>1; 36 if(pos<=mid) ins(ls[x],l,mid,pos,ki,nu); 37 else ins(rs[x],mid+1,r,pos,ki,nu); 38 pushup(x); 39 } 40 int query(int x,int l,int r,int siz){ 41 if(!x||!siz)return 0; 42 if(l==r)return kin[x]; 43 int mid=l+r>>1,res=0; 44 if(ls[x]&&siz<num[ls[x]])res+=query(ls[x],l,mid,siz); 45 else{ 46 res+=kin[ls[x]]; 47 res+=query(rs[x],mid+1,r,siz-num[ls[x]]); 48 } 49 return res; 50 } 51 void cns(int x,int t,int co){ 52 if(!pre[co]){ 53 fro[++tot]=co; 54 pre[co]=t; 55 ins(rt[x],1,m,t,1,1); 56 return ; 57 } 58 if(pre[co]<t){ 59 ins(rt[x],1,m,t,0,1); 60 return ; 61 } 62 if(pre[co]>t){ 63 ins(rt[x],1,m,pre[co],0,1); 64 ins(rt[x],1,m,t,1,1); 65 pre[co]=t; 66 return ; 67 } 68 } 69 void merge(int x,int l,int r,int p){ 70 if(!x)return ; 71 if(l==r){ 72 if(num[x])cns(p,l,dem[l].c); 73 return ; 74 } 75 int mid=l+r>>1; 76 merge(ls[x],l,mid,p); 77 merge(rs[x],mid+1,r,p); 78 } 79 void cl(){ 80 while(tot)pre[fro[tot--]]=0; 81 } 82 }xds; 83 int son[N],siz[N]; 84 int ans[N]; 85 void dfs1(int x,int f){ 86 siz[x]=mp[x].size()+1; 87 for(re i=head[x];i;i=nxt[i]){ 88 int y=to[i]; 89 if(y==f)continue; 90 dfs1(y,x); 91 siz[x]+=siz[y]; 92 if(siz[y]>=siz[son[x]])son[x]=y; 93 } 94 } 95 void dfs(int x,int f){ 96 //cout<<x<<" "<<"sb"<<endl; 97 for(re i=head[x];i;i=nxt[i]){ 98 int y=to[i]; 99 if(y==f||y==son[x])continue; 100 dfs(y,x);xds.cl(); 101 } 102 //cout<<"sb"<<endl; 103 if(son[x])dfs(son[x],x); 104 rt[x]=rt[son[x]]; 105 for(re i=0;i<mp[x].size();i++) 106 xds.cns(x,mp[x][i],dem[mp[x][i]].c); 107 for(re i=head[x];i;i=nxt[i]){ 108 int y=to[i]; 109 if(y==f||y==son[x])continue; 110 xds.merge(rt[y],1,m,x); 111 } 112 ans[x]=xds.query(rt[x],1,m,k[x]); 113 } 114 signed main(){ 115 scanf("%d",&n); 116 for(re i=1;i<n;i++){ 117 int x,y; 118 scanf("%d%d",&x,&y); 119 add_edg(x,y); 120 add_edg(y,x); 121 } 122 for(re i=1;i<=n;i++)scanf("%d",&k[i]); 123 scanf("%d",&m); 124 for(re i=1;i<=m;i++){ 125 scanf("%d%d",&dem[i].x,&dem[i].c); 126 lsh[i]=dem[i].c; 127 } 128 sort(lsh+1,lsh+m+1); 129 lh=unique(lsh+1,lsh+m+1)-lsh-1; 130 for(re i=1;i<=m;i++){ 131 dem[i].c=lower_bound(lsh+1,lsh+lh+1,dem[i].c)-lsh; 132 mp[dem[i].x].push_back(i); 133 } 134 //cout<<"sb"<<endl; 135 dfs1(1,0); 136 dfs(1,0); 137 int q; 138 scanf("%d",&q); 139 for(re i=1;i<=q;i++){ 140 int x; 141 scanf("%d",&x); 142 printf("%d\n",ans[x]); 143 } 144 }
然后就是
T3大佬
题面:辣鸡ljh NOI之后就退役了,然后就滚去学文化课了。
他发现katarina大佬真是太强了,于是就学习了一下katarina大佬的做题方法。
比如这是一本有n道题的练习册,katarina大佬每天都会做k道题。
第一天做第1~k题,第二天做第 2~k+1
题……第n-k+1天做第n-k+1~n
道题。
但是辣鸡 ljh 又不想太累,所以他想知道katarina大佬做完这本练习册的劳累度。
每道题有它的难度值,假设今天katarina大佬做的题目中最大难度为t,那么今天katarina大佬的劳累度就是w[t],做完这本书的劳累值就是每天的劳累值之和。
但是辣鸡ljh一道题都不会,自然也不知道题目有多难,他只知道题目的难度一定在1~m之间随机。
他想让即将参加 NOIP 的你帮他算算katarina大佬做完这本书的劳累值期望
这个题就很有意思,看上去哇塞,他好像有后效性诶,然后我就果断弃掉了,后来发现,以后不能随便放弃某个题
我们先只考虑考虑一天,每个题的难度取值都有m种可能性(先不考虑w)
那么最大值<=1的概率就是g[1]=(1/m)k
<=2的概率就是g[2]=(2/m)k
<=m的概率就是g[m]=1
这不相当于一个前缀和嘛,f[i]=g[i]-g[i-1]
然后我们就把概率求出来了,简单暴了,然后我们就可以直接拿概率*w[i]然后求和
然后再乘上一个(n-k+1)因为一共有这么多天
代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define re register int 4 const int N=505; 5 const int mod=1000000007; 6 int n,m,k; 7 int f[N],g[N],ink; 8 int w[N],ans; 9 int ksm(int x,int y){ 10 int ret=1; 11 while(y){ 12 if(y&1)ret=1ll*ret*x%mod; 13 x=1ll*x*x%mod; 14 y>>=1; 15 } 16 return ret; 17 } 18 signed main(){ 19 scanf("%d%d%d",&n,&m,&k); 20 ink=ksm(ksm(m,k),mod-2); 21 for(re i=1;i<=m;i++){ 22 g[i]=1ll*ksm(i,k)*ink%mod; 23 f[i]=(g[i]-g[i-1]+mod)%mod; 24 scanf("%d",&w[i]); 25 ans=(1ll*ans+1ll*w[i]*f[i]%mod)%mod; 26 } 27 if(k>n)ans=0; 28 ans=1ll*ans*(n-k+1)%mod; 29 printf("%d",ans); 30 }
然后就
T4宝藏
一眼就看出来这个题是状压,然后就不知道该怎么办了
毕竟这么小的数据范围,我还能想到啥
好像这个题暴搜/模拟退火都能过诶
然后我还是老老实实的去状压,
设dp[i][s]为目前最大深度为i,已经可以达到的点的状态为s
然后就有一个转移方程f[i][j]=min(f[i-1][k]+cos(k,j)*(i-1);
还有一些需要预处理的东西,比如由k能否转移到j,比如转移的最小花费是多少;
还有这个题最坑的地方------有重边!!!!
还好我机智,加了一个判断
然后关于为什么可以直接乘(i-1)而不需要考虑其他深度小于(i-1)的点,
因为如果他乘上(i-2)可以造成最优解,那么他一定不会停留在i-2这个点,就会向前转移
所以不需要考虑这些东西
代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 //#define int long long 4 #define re register int 5 const int N=1005; 6 const int S=(1<<12)+10; 7 int n,m; 8 int to[N*2],nxt[N*2],val[N*2],head[N],rp; 9 int edg[15][15]; 10 void add_edg(int x,int y,int z){ 11 to[++rp]=y; 12 val[rp]=z; 13 nxt[rp]=head[x]; 14 head[x]=rp; 15 if(edg[x][y]>z)edg[x][y]=z; 16 } 17 int dp[15][S],minn[S][15],can[S]; 18 void getmin(){ 19 int now[15],dre[15],dnt,cnt,x; 20 for(re i=1;i<(1<<n);++i){ 21 dnt=cnt=0;can[i]=i;x=i; 22 for(re j=1;j<=n;++j) 23 if((i>>(j-1))&1)now[++cnt]=j; 24 else dre[++dnt]=j; 25 for(re j=1;j<=dnt;++j){ 26 for(re k=1;k<=cnt;++k){ 27 if(edg[dre[j]][now[k]]!=0x3f3f3f3f){ 28 //if(edg[dre[j]][now[k]]>10000)cout<<edg[dre[j]][now[k]]<<endl; 29 can[i]|=(1<<(dre[j]-1)); 30 minn[i][dre[j]]=min(minn[i][dre[j]],edg[dre[j]][now[k]]); 31 } 32 } 33 } 34 } 35 } 36 int value(int x,int y){ 37 //cout<<x<<" "<<y<<endl; 38 int z=(y^x),ret=0; 39 //cout<<z<<" "<<endl; 40 for(re i=1;i<=n;++i) 41 if((1<<(i-1))&z){ 42 ret+=minn[x][i]; 43 //cout<<minn[x][i]<<endl; 44 } 45 return ret; 46 } 47 signed main(){ 48 scanf("%d%d",&n,&m); 49 memset(edg,0x3f,sizeof(edg)); 50 memset(minn,0x3f,sizeof(minn)); 51 for(re i=1;i<=m;++i){ 52 int x,y,z; 53 scanf("%d%d%d",&x,&y,&z); 54 add_edg(x,y,z); 55 add_edg(y,x,z); 56 //cout<<edg[x][y]<<" "<<edg[y][x]<<endl; 57 } 58 //cout<<(5^1)<<endl; 59 getmin(); 60 //cout<<can[1]<<endl; 61 memset(dp,0x3f,sizeof(dp)); 62 for(re i=1;i<=n;++i)dp[1][(1<<(i-1))]=0; 63 int ans=dp[1][(1<<n)-1]; 64 //cout<<0x3f3f3f3f<<endl;cout<<dp[1][0]<<endl; 65 for(re i=2;i<=n;++i){ 66 for(re j=1;j<(1<<n);++j){ 67 for(re k=1;k<(1<<n);++k){ 68 if((j&can[k])!=j)continue; 69 if((k&j)!=k)continue; 70 if(dp[i-1][k]==0x3f3f3f3f)continue; 71 dp[i][j]=min(dp[i][j],dp[i-1][k]+value(k,j)*(i-1)); 72 } 73 } 74 //cout<<ans<<endl; 75 ans=min(ans,dp[i][(1<<n)-1]); 76 } 77 printf("%d",ans); 78 }



