CodeTON Round 2/退役划水(18)
这一篇没什么意思,就是自己做了场CF的比赛玩玩
日常做点小水题 防止脑子生锈
不得不说还是CF题有意思
题面放上面,题解放下面,感兴趣的可以想一想
题意:给你一个起始01串和一个目标01串。你每次可以进行操作:取出目前串的前两个字符,然后把它们的或者放回去。问能否通过操作把起始串变成目标串。
复杂度要求
评价:纯纯吓唬人
题意:有道菜,每道菜有个属性。你有个容忍度和食物亲和度。你能吃一道菜当且仅当。你可以随时改变你的亲和度。
现在你要按顺序从号菜吃到号菜。但你懒,问你最少需要改变几次亲和度。
复杂度要求。再多个行不行我也不知道。
评价:有点无聊
C.Virus
题意:有个房子围城一个圈,依次编号到,其中有个房子里的人得了灰指甲,从第一天开始一个传染俩(相邻的两家)。
但是你每天可以选择一户尚未被感染的人,给他们用亮甲,这样他们以后就再也不会得灰指甲了。(已经感染的就摆烂了)
问如果你亮甲用的好的话最少有几户得了灰指甲的。
复杂度要求(n很大)
评价:你看我都这么翻译题面了这题能无聊吗
题意:有一个数列长为,有个人,其中有恰好一个人是笨比。
除了笨比以外,所有人可以按照这个方法操作数列:任选,使。每人至少操作一次
笨比也听了,但是笨比毕竟是笨比,他每次是使。他也至少操作了一次
现在给你个被操作后的数列,问哪个是笨比数列,同时还问这个数列被笨比操作了多少次。
复杂度要求
评价:尚且算有趣的脑洞题,但是脑洞并不大(感觉之前似乎见过)
题意:有一个,且只有恰好一个点其出度为。每个点都有一个非负权值(可以是)
在每一秒开始时,你都会记录下所有权值非的点,这些点构成的集合称为。
此后,对于中的每个点,你会先使减少,然后使的所有出边指向的点其增加
由于是所以这些数最后一定都会从出度为的那个点流出(消失)。问多少秒之后所有点的权值都变成了。
复杂度要求。初始权值可以很大。
评价:更无聊一些的脑洞题。要注意考虑到那唯一的出点可能有了一段时间的权值之后又没有了之后又有了。
题意:两个人在一个长度为的序列上博弈。最开始序列中每个位置要么是要么是。先手
每次轮到行动时,需要选择相邻的两个位置,且这两个位置中至少要有一个位置是,然后把这两个位置都变成空的
轮到时也类似,不过选的位置至少要包含一个。要注意,选择的位置可以包含空的,只要另一个格子有自己要的就行。
(如选择的位置可以是这几种,下划线表示空)
轮流来,谁不能行动了谁就输了。问最优策略下谁会赢
复杂度要求
评价:很不错的思维题。很有意思。很博弈。也很搞心态。
G.没看
H1.懒得写(似乎是个多项式的模板题)
H2.不会
题解区(我没看官方题解)
A.
你每次操作只能动最靠左的两个数,每次还会使长度缩短1。
那右边的字符肯定是没法改变的了,你只能操作恰好次(分别是起始和目标串长度)来决定操作结果的第一个字符。
剩下的个字符是固定的,如果目标串和起始串的最后个字符不一样那就直接
然后前面这个说得玄乎,但你可以自行决定的话那其实就相当于保留两个中你想要的一个
那肯定只要出现过就可以一直保留到最后了。没出现过那一定就不行
检查一下目标串的第一位在初始串的前位中是否出现过就好了
就这么简单个东西用了分钟,我好菜

1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m,t; 4 char s[1000],d[1000]; 5 int main(){ 6 cin>>t; 7 while(t--){ 8 cin>>n>>m>>s>>d; 9 for(int i=1;i<m;++i) if(s[n-i]!=d[m-i]) goto fail; 10 for(int i=0;i<=n-m;++i) if(s[i]==d[0]) goto succ; 11 puts("NO"); continue; 12 succ: puts("YES"); continue; 13 fail: puts("NO"); 14 } 15 }
B.
你要用最少的次数,那肯定就要每一次尽量多的吃。
想吃一个连续区间的食物,你需要这个区间里的所有食物的不超过,这样你就可以把你的调整成和的平均值了
每次最多能吃多少?单调性很明显。二分即可。每次检查一个区间能否一次吃完,写一个表来搞区间查极值即可
赛后发现可以写线段树上二分。复杂度一样,也一样的无聊
但是人菜手生,就俩的玩意写了分钟,我好菜

1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,v,t,mx[20][633333],mn[20][633333], hb[633333]; 4 int Max(int l, int r){return max(mx[hb[r-l+1]][l],mx[hb[r-l+1]][r-(1<<hb[r-l+1])+1]);} 5 int Min(int l, int r){return min(mn[hb[r-l+1]][l],mn[hb[r-l+1]][r-(1<<hb[r-l+1])+1]);} 6 int main(){ 7 cin>>t; 8 for(int i=0; i<19; ++i) for(int j=1<<i; j<1<<i+1; ++j) hb[j]=i; 9 while(t--){ 10 cin>>n>>v; 11 for(int i=1;i<=n;++i) scanf("%d",&mx[0][i]),mn[0][i]=mx[0][i]; 12 for(int i=1;i<19;++i) for(int j=1;j<=n;++j) mx[i][j]=max(mx[i-1][j],mx[i-1][j+(1<<i-1)]), mn[i][j]=min(mn[i-1][j],mn[i-1][j+(1<<i-1)]); 13 int p=1, c=0; 14 while(p<=n){ 15 //cerr<<p<<' '<<c<<endl; 16 int l=p, r=n, m, a=p; 17 while(m=l+r>>1,l<=r) if(Max(p,m)-Min(p,m)<=v+v) a=m, l=m+1; else r=m-1; 18 c++; p=a+1; 19 } 20 cout<<c-1<<endl; 21 } 22 }
C.
其实也并没有有趣到哪里去
你每次选择一个房子保护起来,你所选择的一定是已经感染和尚未感染的分界线上的房子
不然你留出若干空位第二天也一定会被感染了
这题从已感染的房子的角度出发并不方便,所以应该从 尚未被感染的连续区间考虑(区间个数也是个)
那么显而易见的,如果你什么也不做,那么每过去一天,所有区间的两端都会被感染,区间长度(直到为)
然后如果你去对一个区间保护了一次(也就是把病毒从一头堵上了)那么久只会从另一头传染,区间长度的缩短速率由变成
再操作一次那么中间这一段就被堵上了,速率降为。剩余的整段区间都被保护下来了。
决策也就比较明显了,把所有区间按照从长到短的顺序依次排序,然后画天时间去保护第一段,后天保护第二段…能保护下户(从开始给段编号)
最后边界情况是区间长度小于等于的时候,你再去保护也就能护下来恰好个了。和上面的情况用一样的公式会出问题
(这里还了一发,不过是样例所以没扣分)
思路上也不算难,但我脑子锈了,用了分钟,我好菜

1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m,t,a[233333],b[233333]; 4 int main(){ 5 cin>>t; 6 while(t--){ 7 cin>>n>>m; 8 for(int i=1;i<=m;++i) scanf("%d",&a[i]); 9 sort(a+1,a+1+m); 10 for(int i=1;i<m;++i) b[i]=a[i+1]-a[i]-1; 11 b[m]=n+a[1]-a[m]-1; 12 sort(b+1,b+1+m); 13 reverse(b+1,b+1+m); 14 int ans=0; 15 for(int i=1;i<=m;++i) ans+=b[i]-i-i-i-i+4==1?1:max(0,b[i]-i-i-i-i+3); 16 cout<<n-ans<<endl; 17 } 18 }
D.
那肯定是要找两种操作的区别了。
我们希望找到一种特征值,使得所有正常人的序列的特征值是一样的,笨比的特征值与众不同。
同时最好能通过笨比的特征值和普通人特征值的差距能反映出笨比的操作次数。
因为普通人操作次数彼此之间不一定相同,但是我们希望特征值相同,所以操作一次最好能不改变特征值
来看具体的操作,实际上就是把某一个数值所在的下标,把某个数值所在的下标,保证不越界
这样说的话就很自然了,我们定义特征值就是所有数值的下标和,那么操作的时候显然是不变的,也就是
然后再看笨比,实际上就是把某一个数值所在的下标,把某个数值所在的下标,同样不会越界
那么也就是每次操作特征值会.这样就完事了,找到特征值最大的那个,用他减掉普通人的特征值就是笨比的操作次数了
还挺有意思的,有点套路,但我还是用了分钟,我好菜

1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m,t; long long a[233333],x; 4 int main(){ 5 cin>>t; 6 while(t--){ 7 cin>>n>>m; 8 for(int i=1;i<=n;++i) a[i]=0; 9 for(int i=1;i<=n;++i) for(int j=0;j<m;++j) scanf("%lld",&x), a[i]+=j*x; 10 if(a[1]!=a[2]){if(a[3]==a[1]) cout<<"2 "<<a[2]-a[1]<<endl; else cout<<"1 "<<a[1]-a[2]<<endl;} 11 else for(int i=3;i<=n;++i) if(a[i]!=a[1]) cout<<i<<' '<<a[i]-a[1]<<endl; 12 } 13 }
E.
直接模拟肯定是不行的,权值一大直接起飞了
然后你可能就会考虑直接算出到达唯一没有出边的点的总流量是多少,再和最早到达这个点的流量到达所需要的时间加起来这类的
这种思路默认了一旦开始有流量,以后就都有了。但事实并不是这样
考虑一种情况
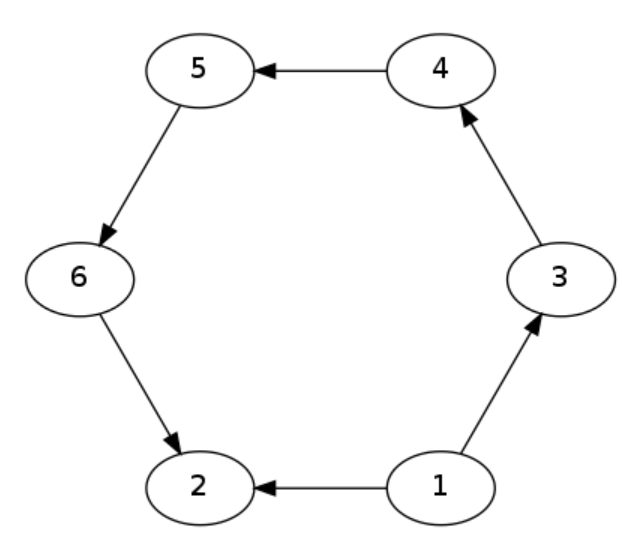
假如最开始只有号点有的权值。
它会在秒后和秒后分别给号点产生的流量。中间的几秒流量断掉了
然后就卡住了,我好菜
但没完全卡住。把上面的思路结合起来。由于中的最长路长度也只有
所以我们只要模拟前轮,此后所有流量到唯一无出度点的路径就都已经流通了
此后流量一断就说明全图已经没有流量了。在流了轮的图上直接算出此后到目标点的总量,加上即为答案
由于我是笨比,我以为拓扑之后入度就已经被清空了我就没再手动清空,但实际上如果模拟的轮数里就直接结束了就会直接跳过拓扑,怒一发交罚时
暴力简单,错解也简单。暴力+错解我就做了长达分钟,我好菜

1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m,t,a[1234],q[1234],ind[1234]; 4 vector<int>v[1222]; 5 #define mod 998244353 6 int main(){ 7 cin>>t; 8 while(t--){ 9 cin>>n>>m; 10 for(int i=1;i<=n;++i) scanf("%d",a+i); 11 for(int i=1,x,y;i<=m;++i) cin>>x>>y, v[x].push_back(y), ind[y]++; 12 int ans=0; 13 while(ans<n){ 14 int t=0; 15 for(int i=1;i<=n;++i) if(a[i]) q[++t]=i; 16 if(t==0) break; 17 for(int i=1;i<=t;++i){ 18 a[q[i]]--; 19 for(auto x:v[q[i]]) a[x]++; 20 } 21 ans++; 22 } 23 int t=0; 24 if(ans<n) {printf("%d\n",ans); goto xxx;} 25 for(int i=1;i<=n;++i) if(!ind[i]) q[++t]=i; 26 for(int h=1;h<=t;++h){ 27 //cerr<<"!!!"<<h<<endl; 28 int x=q[h]; 29 if(h==n) printf("%d\n", (a[x]+n)%mod); 30 for(auto y:v[x]){ 31 (a[y]+=a[x])%=mod; 32 ind[y]--; 33 if(!ind[y]) q[++t]=y; 34 } 35 } 36 xxx: 37 for(int i=1;i<=n;++i) v[i].clear(), ind[i]=0; 38 } 39 }
F.
只会知识的人做着费劲,只会乱搞的人做着费劲,就我这种一瓶子不满半瓶子晃的运气好搞出来了(?)
我游戏打多了。不妨认为序列上的数量就是玩家的血量。同理
按照题意,每次行动自己必定扣点血,如果选的是这样的,那么就会给对方也扣点血
讲道理选会给自己扣点血,但是显而易见的,他不会这么选
由于可以选空了的位置或者是,那么一定更乐意自己只扣点血
(除非全屏都是而没有,这种情况扣血就扣血吧,反正赢定了)
轮到谁的时候如果他没血了他就输了。
那么现在决策只有两种:同时扣双方点血,或者只有自己扣点血
那么显然前者更优。在所有的都被选完后,双方就只能每回合扣自己点血,直到一方没血
那么很明显了,最开始的阶段每回合双方都扣血,后来双方每回合都扣血
那么谁血多谁赢呗
好了,这题你已经完成了了(
血相同怎么办?
会发现,不同位置的选了之后的效果是不一样的
如对于串,如果吃掉中间的变成那么他就赢了,如果吃掉靠边的变成那么他就输了
只有这样的交替串会有这样不同的决策
我们认为有个字母的交替串的长度为(因为实际上可操作的方案数是,所以这样更方便)
那么长度为的交替串的所有决策就是,使长度变为(吃边缘),或者拆分成长度为和的两个串(吃中间)
味太重了。一看就是函数题。把所有的串异或起来就是最终的值
如果整个串就是一个交替串,那么直接取这个交替串的值就好了
如果不止是一个交替串,那么就把它划分成多个交替串。如拆分成也就是长度分别为的交替串
把它们的值异或起来,非就必胜。完结撒花
然而还没等你撒出去你就发现这算的复杂度是的
那就打个表看看有没有规律吧:
(这是我手动打表的范围)
嗯?看不出来吧?
(这是机器打表你有耐心看的范围)
如果你是正常人我估计你还是什么也看不出来。
事实上把表翻到后头会好看一些:(下面这是从第项开始)
现在能看出来了吗?
然而你们是在打,但我是在打网络线上赛。

然后结果属实是震惊到我了

周期长达的,前两个周期乱掉的一个周期序列
这能看出个毛线啊
反正最后我就抬走了
但这个题我居然用了分钟,我太菜了

1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m,t,a[1234],q[1234],ind[1234]; 4 char s[533333]; 5 int f[]={8, 1, 1, 2, 0, 3, 1, 1, 0, 3, 3, 2, 2, 4, 4, 5, 5, 9, 3, 3, 0, 1, 1, 3, 0, 2, 1, 1, 0, 4, 5, 3, 7, 4}; 6 int get(int x){ 7 switch(x){ 8 case 0:return 0; 9 case 14:return 0; 10 case 16:return 2; 11 case 17:return 2; 12 case 31:return 2; 13 case 34:return 0; 14 case 51:return 2; 15 default:return f[x%34]; 16 } 17 } 18 int main(){ 19 cin>>t; 20 while(t--){ 21 cin>>n>>s; 22 int ans=0; 23 for(int i=0;i<n;++i) ans+=s[i]=='R'?1:-1; 24 s[n]=s[n-1]; 25 if(ans>0)puts("Alice"); 26 else if(ans<0)puts("Bob"); 27 else{ 28 for(int i=1,c=0;i<=n;++i) if(s[i]!=s[i-1]) c++; else ans^=get(c),c=0; 29 puts(ans?"Alice":"Bob"); 30 } 31 } 32 }


好耶,变成深橙名了
看来红名真的是有手就行,即便是菜如我
算了还是别乱说了毕竟我还没红(((
DC老矣,尚能饭否 不能饭了 太下饭了
打什么算法竞赛,不如回家睡大觉
啊我就在家啊,那我睡觉了





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)