[考试反思]0613四校联考第三轮day2：生活

终于把博客补全了/px

然而这场考得也好不到哪里去，写了四篇博客然而四场都是炸的。怪自闭的

说实在的这场至少分数不算低，还是可以接受的（谁要你自己接受啊

$T1$几乎可以说是很套路的题了，但是花的时间还是有点长了

然后$T2$数据非常水导致我写的随机化过了子任务$1,9,10$而剩下的$PC$了

$T3$很早就想到了$O(n^3)$的做法，但是因为数据很有梯度于是一直执着于卡常。

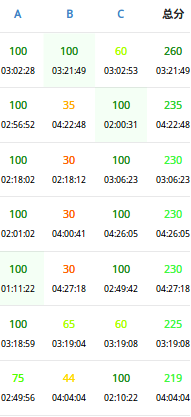
估分$64/68$那样，本机跑$64$的数据是$0.26s$交上去还是被卡了，我人都傻了

然而菜就是菜，搞得好像多$4pts$对我有什么影响一样

这一轮的两场下来，主要还是因为$day1$炸的太厉害了，所以总分依旧滚的有点远，貌似还是会被挤来挤去到退役线之外

教练说不要太看重模拟赛成绩所以其实我也没仔细研究。的确没必要

模拟赛只是在为以后各方面积累经验而已，在某些方面有提升这就足够了

 

T1：A

大意：$w\times h$的点阵，从中选取$n$个点在一条直线上的方案数。$w,h \le 10^5$

思路挺多的，比较可行的一个是枚举起点和终点然后在线段上的点中选取$n-2$。因为起点终点不同所以一定不重不漏。

然后发现其实我们只要枚举终点-起点这个向量就足够了。首先平行与坐标轴的特判掉，剩下的就是斜向左下或右下的两种。

等价的，只计数一种然后乘二就可以了。式子大约长这样：

$\sum\limits_{i=1}^{w} \sum\limits_{j=1}^{h} \binom{gcd(i,j)-1}{n-2} (w-i+1)(h-j+1)$

$=\sum\limits_{g=1}^{max(w,h)} \binom{g-1}{n-2} \sum\limits_{i=1}^{\frac{w}{g}} (w-ig+1) \sum\limits_{j=1}^{\frac{h}{g}} (h-jg+1) [gcd(i,j)=1]$

$=\sum\limits_{g=1}^{max(w,h)} \binom{g-1}{n-2}  \sum\limits_{i=1}^{\frac{w}{g}} \sum\limits_{j=1}^{\frac{h}{g}}  \sum\limits_{d|i,d|j} \mu(d) (w-ig+1) (h-jg+1)$

$=\sum\limits_{g=1}^{max(w,h)} \binom{g-1}{n-2}  \sum\limits_{d=1}^{\frac{max(w,h)}{g}} \mu(d) \sum\limits_{i=1}^{\frac{w}{gd}} \sum\limits_{j=1}^{\frac{h}{gd}}(w-igd+1) (h-jgd+1)$

$=\sum\limits_{gd=1}^{max(w,h)} \sum\limits_{g|dg} \binom{g-1}{n-2} \mu(\frac{gd}{g}) cal(w,gd) cal(h,gd)$

对于每种$gd$，$O(n\ ln\ n)$处理前半部分。后面的$cal$是$O(1)$的（等差数列求和），然后就可以直接做了。

#include<bits/stdc++.h>
using namespace std;
const int $=1e5+5,mod=323232323;
int fac[$],inv[$],mu[$],np[$],p[$],pc,F[$],ans,w,h,n;
int qp(int b,int t,int a=1){for(;t;t>>=1,b=1ll*b*b%mod)if(t&1)a=1ll*a*b%mod;return a;}
int C(int b,int t){return 1ll*fac[b]*inv[t]%mod*inv[b-t]%mod;}
int cal(int n,int d){int t=n/d;return (t*(n+1ll)-d*(t+1ll)*t/2)%mod;}
int main(){
    freopen("a.in","r",stdin); freopen("a.out","w",stdout);
    for(int i=fac[0]=1;i<$;++i)fac[i]=fac[i-1]*1ll*i%mod;
    inv[$-1]=qp(fac[$-1],mod-2);
    for(int i=$-2;~i;--i)inv[i]=inv[i+1]*(i+1ll)%mod;
    mu[1]=1;
    for(int i=2;i<$;++i){
        if(!np[i])mu[i]=-1,p[++pc]=i;
        for(int j=1,x;(x=i*p[j])<$;++j)
            if(i%p[j])mu[x]=-mu[i],np[x]=1;
            else{np[x]=1;break;}
    }
    scanf("%d%d%d",&w,&h,&n); if(w>h)swap(w,h); w--;h--;
    if(n==1)return printf("%lld",(w+1ll)*(h+1)%mod),0;
    for(int g=n-1;g<=h;++g)for(int x=g;x<=h;x+=g)F[x]=(F[x]+mu[x/g]*C(g-1,n-2))%mod;
    for(int g=1;g<=h;++g)ans=(ans+F[g]*1ll*cal(w,g)%mod*cal(h,g))%mod;ans=ans*2%mod;
    ans=(ans+(w+1ll)*C(h+1,n)+(h+1ll)*C(w+1,n))%mod;
    printf("%d",(ans+mod)%mod);
}

 

T2：B

大意：长为$n$的数轴上有$n$条线段，你要选择尽量少的点使得每条线段上都有点。你要把每条线段分配给在线段上的一个点。

代价是线段中点到你所选的点的距离的二倍。最小化点数的基础上最小化代价。$n \le 5 \times 10^5$

首先最小化点数还是比较简单的：直接贪心，一直咕咕咕，能不放点就不放点，也就是线段按照右端点排序，如果当前左端点已经被覆盖就没事，否则就在右端点放一个。

最小化代价就比较困难了：考虑$dp$

首先有一个结论：按照刚才贪心的过程按所有右端点把数轴砍成若干段。除了最后一段，每段中恰好选一个。

那么$O(n^2)dp$就可以随便写了。然后还有一个结论：决策单调性。

用那种$solve(l,r,L,R)$做就可以了。时间复杂度$O(n\ log\ n)$

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int $=1e6+5;
int n,mxl[$],p[$],ans; ll cnt[$],sum[$],dp[$],Ans=1e18;
struct L{int l,r;}_[$];
ll cal(int l,int r){int m=l+r>>1;return mxl[r-1]>l?1e17:r*(cnt[r]-cnt[m])-(sum[r]-sum[m])+(sum[m]-sum[l])-l*(cnt[m]-cnt[l])+dp[l];}
void solve(int l,int r,int L,int R){
    int m=L+R>>1,P; if(R<L)return;
    for(int i=l;i<=r;++i)if(cal(i,m)<dp[m])dp[m]=cal(P=i,m);
    solve(l,P,L,m-1);solve(P,r,m+1,R);
}
int main(){
    freopen("b.in","r",stdin); freopen("b.out","w",stdout);
    scanf("%d",&n); for(int i=1,l,r;i<=n;++i)scanf("%d%d",&l,&r),l<<=1,r<<=1,_[i]=(L){l,r},mxl[r]=max(mxl[r],l),cnt[l+r>>1]++,sum[l+r>>1]+=l+r>>1;
    sort(_+1,_+1+n,[](L x,L y){return x.r<y.r;});
    for(int i=1;i<=n;++i)if(_[i].l>p[ans])p[++ans]=_[i].r;
    n<<=1; memset(dp,63,sizeof dp);
    for(int i=1;i<=n;++i)cnt[i]+=cnt[i-1],sum[i]+=sum[i-1],mxl[i]=max(mxl[i],mxl[i-1]);
    for(int i=1;i<=p[1];++i)dp[i]=i*cnt[i]-sum[i];
    for(int i=2;i<=ans;++i)solve(p[i-2]+1,p[i-1],p[i-1]+1,p[i]);
    for(int i=p[ans-1]+1;i<=n;++i)if(mxl[n]<=i)Ans=min(Ans,dp[i]+sum[n]-sum[i]-(cnt[n]-cnt[i])*i);
    printf("%d %lld",ans,Ans);
}

 

T3：C

大意：求满足$dfs$序为$i$的点的子树大小$\ge A_i$的树的个数。$n \le 10^4$

首先子树中$dfs$序是连续的，那么如果有两条限制$[i,i+A_i)$和$[j,j+A_j)$是相交的，如若$i<j<i+A_i<j+A_j$。

那么对$i$的限制也可以调整为$[i,j+A_j)$。也就是说相交关系可以转化为包含。那么也就是说只剩下了不相交和包含两种关系。可以建树了。

具体的实现方法是：倒着扫一遍并且维护一个栈，每次尝试与栈顶合并即可。

建出树之后就是：一个点的所有儿子的确都是它的儿子，所有儿子之间不相交。

我们考虑合并两棵树并保证第一棵树的$dfs$序严格小于第二个，我们发现，第二棵树的根只能接在第一棵树的最右侧的一条链的最右侧那些点上。

我们称之为右链。设$dp[i][j]$表示当前在处理$i$的限制区间，当前右链长度为$j$。转移没啥问题。

链长的限制是子树大小，所以时间复杂度是子树合并。总时间复杂度是$O(n^2)$

#include<bits/stdc++.h>
using namespace std;
const int $=10001,mod=323232323;
int ans,n,a[$],f[$][$],st[$],tp,sz[$],g[$]; vector<int>E[$];
int mo(int x){return x>=mod?x-mod:x;}
void dfs(int p){
    f[p][0]=1; sz[p]=1;
    for(int y:E[p]){
        dfs(y);
        for(int i=sz[p]-1;~i;--i)f[p][i]=mo(f[p][i]+f[p][i+1]);
        for(int i=0;i<sz[p];++i)for(int j=0;j<sz[y];++j)g[i+j+1]=(g[i+j+1]+1ll*f[p][i]*f[y][j])%mod;
        sz[p]+=sz[y];
        for(int i=0;i<sz[p];++i)f[p][i]=g[i],g[i]=0;
    }
}
int main(){
    freopen("c.in","r",stdin); freopen("c.out","w",stdout);
    scanf("%d",&n); for(int i=1;i<=n;++i)scanf("%d",&a[i]),a[i]=i+a[i]-1; a[1]=n;
    for(int i=n;i;--i){
        while(tp&&st[tp]<=a[i])a[i]=max(a[i],a[st[tp]]),E[i].push_back(st[tp]),tp--;
        st[++tp]=i; if(a[i]>n)return puts("0"),0;
    }dfs(1);for(int i=0;i<n;++i)ans=mo(ans+f[1][i]); printf("%d",ans);
}