[考试反思]0418省选模拟74：杂枝

好像现在乱搞已经在心里扎根了。

三道题的暴力分给的都很足，暴力写满大约是$60+60+33=153$。思维难度都不大。

然而$T2$我是怎么判断这是否为一个菊花的呢？

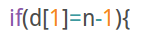
除非$n=1$，万物皆菊花。

然后就只得到了判菊花的$20$，链的$10$和纯暴力的$30$都没了。

无话可说，只能

然后是$T3$，这次的强制在线是$x=(x\xor lastans)\mod n +1$。

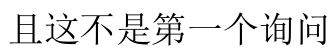
所以那个$+1$就炸掉了。还能有$25$实属不易。

反正就是极度弱智的一场，写了三个暴力挂了俩，想乱搞一分没多拿。

而且这次的正解貌似都不算难但是一个都没想（可能都没花多少时间思考。。

俩结论一分块（虚树什么的还是算了）

又开始了分数是黄色的时光。。。

 

T1：签到

大意：网格左上出发走到右下，可以重复经过一个点（包括右下），最大化 经过次数为奇数的点 的权值 的异或和。$n,m \le 500,w_i \le 10^9$

大约是结论题：只要任意选出的点个数与$n+m-1$奇偶性相同，那么这些点的异或和就是一种合法路径的权值。

大致理解就是：先随便走一条覆盖了所有点的路径（可覆盖多次），然后对于路径上任意点$A,B$我们可以在经过点$A$时，

沿任意路径$s$走到$B$后再沿路径$s$折返回$A$。中间所有点都往返共经过了$2$次，只有$A,B$恰好多经过了一次。

也就是说我们可以任选两个点将其取反。所以结论成立。

所以问题是：你可以在$nm$个值中任选奇数/偶数个，最大化异或和。

怎么限制选的个数的奇偶呢？我们把所有数的最高位赋为$1$。这样如果你选了奇数个，最高位就会是$1$否则为$0$

所以只要根据奇偶最开始查询线性基是否带有最高位的$1$就可以直接做了。

#include<bits/stdc++.h>
using namespace std;
#define S 13666663
int n,m,ans,b[32];
void ins(int x){for(int i=30;~i;--i)if(x&1<<i)if(b[i])x^=b[i];else b[i]=x,x=0;}
int main(){
    cin>>n>>m;
    for(int i=1,x;i<=n*m;++i)scanf("%d",&x),ins(x|1<<30);
    ans=(n+m&1)<<30;
    for(int i=30;~i;--i)if(!(ans&1<<i))ans^=b[i];
    cout<<ans-(1<<30)<<endl;
}

 

T2：树（tree）

大意：多次询问求$\min\limits_{i=l}^{r} dis(i,x)$。$n,q \le 10^5$

首先正解的做法就是，像线段树一样把询问离线下来撒在$log$个区间上。

然后对于每个区间，把区间内所有点和询问点一起拿出来建虚树

写的好的话是$O(n\ log\ n)$。

考虑另一个简单粗暴的分块做法：

求出$dp[i][j]$表示第$i$块内的所有点到$j$的最小距离。这个可以直接换根$dp$。对于每一个块$O(n)$得到

然后零散部分暴力查询（预处理，弄个$O(1)lca$就成）

思路非常简单粗暴。时间复杂度$O(n \sqrt{n})$。需要注意常数。代码比较好写。

一个显而易见的剪枝：先查询整块（更新答案的概率大）如果边缘块的最小值无法更新答案则直接跳出（$O(1)lca$常数不小）

#include<bits/stdc++.h>
using namespace std;
#define S 200002
#define L 800
int fir[S>>1],l[S],to[S],w[S],ec,n,q,ST[18][S],dfn[S>>1],tim,dep[S>>1],dp[S/2/L+1][S>>1],B,bit[S];
void link(int a,int b,int v){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;w[ec]=v;}
void pre(int p,int fa){
    ST[0][dfn[p]=++tim]=dep[p];
    for(int i=0;i<=B;++i)dp[i][p]=0x3fffffff; dp[p/L][p]=0;
    for(int i=fir[p];i;i=l[i])if(to[i]!=fa){
        dep[to[i]]=dep[p]+w[i],pre(to[i],p),ST[0][++tim]=dep[p];
        for(int j=0;j<=B;++j)if(dp[j][p])dp[j][p]=min(dp[j][p],dp[j][to[i]]+w[i]);
    }
}
int dis(int a,int b){
    a=dfn[a];b=dfn[b];if(a>b)swap(a,b); int B=bit[b-a+1];
    return -min(ST[B][a],ST[B][b-(1<<B)+1])<<1;
}
void dfs(int p,int fa){
    for(int i=fir[p];i;i=l[i])if(to[i]!=fa){
        for(int j=0;j<=B;++j)dp[j][to[i]]=min(dp[j][to[i]],dp[j][p]+w[i]);
        dfs(to[i],p);
    }
}
int in(){int p=0;char ch=getchar();
    for(;!isdigit(ch);ch=getchar());for(;isdigit(ch);ch=getchar())p=p*10+ch-48;
    return p;
}
int main(){//freopen("game10.in","r",stdin);freopen("0.out","w",stdout);
    n=in();
    for(int i=1,a,b,v;i<n;++i)a=in()-1,b=in()-1,v=in(),link(a,b,v),link(b,a,v);
    B=(n-1)/L; pre(0,-1); dfs(0,-1);// return 0;
    for(int i=1;i<18;++i)for(int j=1;j+(1<<i)-1<=tim;++j)ST[i][j]=min(ST[i-1][j],ST[i-1][j+(1<<i-1)]);
    for(int i=0;i<18;++i)for(int j=1<<i;j<1<<i+1&&j<=tim;++j)bit[j]=i;
    cin>>q; while(q--){
        int l=in()-1,r=in()-1,x=in()-1,ans=0x3fffffff;
        if(l<=x&&x<=r){puts("0");continue;}
        if(l/L==r/L)for(int i=l;i<=r;++i)ans=min(ans,dis(i,x)+dep[i]);
        else{
            for(int i=l/L+1;i<r/L;++i)ans=min(ans,dp[i][x]-dep[x]);
            if(dp[l/L][x]<ans+dep[x])for(int i=l/L*L+L-1;i>=l;--i)ans=min(ans,dis(i,x)+dep[i]);
            if(dp[r/L][x]<ans+dep[x])for(int i=r/L*L;i<=r;++i)ans=min(ans,dis(i,x)+dep[i]); r=r/L-1;
        }printf("%d\n",ans+dep[x]);
    }
}

 

T3：区间（interval）

大意：在线多区间并数颜色。$n ,\sum k \le 10^5$。空间限制$8MiB$

数颜色好像一直没什么好的方法，一在线做法就很少了，再卡一下空间主席树就死了。

好像就剩$O(n^2)$的做法了？那只能$bitset$了啊。

分块$bitset$看起来很优秀，然而合并代价过大，可能就是$O(n^{2.5})$的了。

然后听$dkk$大神讲了$Method\ of\ 4\ Russians$。名字挺神奇的，但是大概意思就是分块+数据结构维护块之间。

有什么优秀的数据结构，可以快速查询区间或和呢？$ST$表。

假如我们的块长为$L$，那么我们最终单次询问的复杂度是：

两侧暴力查询（单点修改$bitset$）：$O(L)$

中间$ST$表区间查询（需要$bitset$或）：$O(\frac{n}{64})$

预处理的复杂度是$O(\frac{n}{64} \times \frac{n}{L} log\frac{n}{L})$

总空间消耗与预处理的时间复杂度是相同的。

权衡之下，最优的块长是$\frac{n}{64}$。

所以只要手写个$bitset$就可以过去了。

也可以优化，把序列中只出现了一次的颜色提出去单独计算，那么剩余的值域范围至少减半。

#include<bits/stdc++.h>
using namespace std;
#define S 100005
int a[S],c[S],n,W,N,L,cb[65536],q,op,fi,la,rb[64],ans;
struct bit{
    unsigned long long b[782];
    void operator|=(bit&z){for(int i=(N-1>>6)+1;~i;--i)b[i]|=z.b[i];}
    int cnt(int a=0){for(int i=(N-1>>6)+1;~i;--i)a+=cb[b[i]&65535]+cb[b[i]>>16&65535]+cb[b[i]>>32&65535]+cb[b[i]>>48&65535];return a;}
}ST[7][64],Y,R;
struct qry{int l,r;friend bool operator<(qry a,qry b){return a.l<b.l;}}Q[S];
void cal(int l,int r){
    if(l/L==r/L){for(int i=r;i>=l;--i)if(~a[i])R.b[a[i]>>6]|=1ll<<(a[i]&63);else ans++;}
    else{
        for(int i=l/L*L+L-1;i>=l;--i)if(~a[i])R.b[a[i]>>6]|=1ll<<(a[i]&63);else ans++;
        for(int i=r/L*L;i<=r;++i)if(~a[i])R.b[a[i]>>6]|=1ll<<(a[i]&63);else ans++;
        l=l/L+1;r=r/L-1;
        if(l<=r){int z=rb[r-l+1];R|=ST[z][l];R|=ST[z][r-(1<<z)+1];}
        for(int i=l;i<=r;++i)ans+=c[i];
    }
}
int main(){
    //freopen("0.in","r",stdin);freopen("3.out","w",stdout);
    cin>>n>>q>>op;
    for(int i=0;i<n;++i)scanf("%d",&a[i]),c[a[i]]++;
    for(int i=0;i<n;++i)if(c[a[i]]==1)a[i]=-1;
    for(int i=0;i<n;++i)if(~a[i])c[++N]=a[i];
    sort(c+1,c+1+N); N=unique(c+1,c+1+N)-c;
    for(int i=0;i<n;++i)if(~a[i])a[i]=lower_bound(c+1,c+N,a[i])-c-1;
    L=(n-1>>6)+1;
    for(int i=0;i<64;++i)c[i]=0;
    for(int i=0;i<64;++i)for(int j=i*L;j<i*L+L&&j<n;++j)if(~a[j])ST[0][i].b[a[j]>>6]|=1ll<<(a[j]&63);else c[i]++;
    for(int i=1;i<7;++i)for(int j=0;j+(1<<i)<=64;++j)ST[i][j]=ST[i-1][j],ST[i][j]|=ST[i-1][j+(1<<i-1)];
    for(int i=1;i<65536;++i)cb[i]=cb[i^i&-i]+1;
    for(int i=0;i<7;++i)for(int j=1<<i;j<1<<i+1&&j<65;++j)rb[j]=i;
    for(int _=1;_<=q;++_){
        int k;ans=0;scanf("%d",&k);
        for(int i=1;i<=k;++i){
            int l,r;scanf("%d%d",&l,&r);
            if(op&&fi){l=(l^la)%n;r=(r^la)%n;if(l>r)swap(l,r);}else l--,r--;
            Q[i]=(qry){l,r};
        }
        sort(Q+1,Q+1+k);
        for(int i=2;i<=k;++i)if(Q[i].l<=Q[i-1].r+1)Q[i].r=max(Q[i-1].r,Q[i].r),Q[i].l=Q[i-1].l;else cal(Q[i-1].l,Q[i-1].r);
        cal(Q[k].l,Q[k].r);
        fi=1;printf("%d\n",la=ans+R.cnt());R=Y;
    }
}