[考试反思]0219省选模拟26:精准
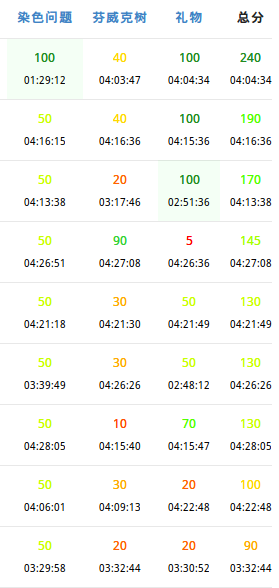

第一次精准估分。三道题和估分都完全一样。
如果说这是个好事的话。。。
那我未免估的太低了点
没丢冤枉分自然是好事,可是没丢冤枉分排名还这么低就有点说不过去了。
时间分配和难易度判断又有些失误,上来看$T1/3$都想多项式全家桶+生成函数。
然后把自己恶心到了。然后$T2$看起来像大数据结构也恶心,结果就不知道把时间用在哪里了。
相对简单的T3$基本没留时间想。整场的分也就没高的理由。
T1:染色问题
大意:$n$长序列,$m$种颜色依次染一个非空连续区间,求最后每个位置都有颜色的序列的不同的序列数。$n,m \le 10^6$
好题。
依次染有点麻烦,倒着想,每次是在未被染色的地方染一个连续可空区间,第一次不可空。
这很$dp$。设$i$轮后还有$j$位置未染的方案数,则$dp_{i,j}=dp_{i-1,j}+(j+1)\sum\limits_{k=j+1}$^{n} dp_{i-1,k}$
前缀和优化就可以拿到暴力分。
转移很奇怪。第一部分系数为$1$,是一个位置也没有染,类似于传递。
第二种是给所有染色的情况的方案数乘了$(j+1)$。也就是染色后剩余空白位置的个数$+1$,类似与传递过程中的落脚点。
也就是对于每个(出现了哪些颜色)的方案,其贡献是落脚点编号之积,且没有落脚次数限制。
于是我们枚举最后实际出现了$i$种颜色,是个组合数(注意最后一种一定出现),然后要得就是(任选$i$个落脚点的积)的和。
形式有点像背包。于是我们设计一个类似于生成函数的东西,把落脚点作为物品放进去
(只不过这次大小是1但是我们为了方便把方案放在了常数上,最后的指数也就反了过来)
也就是$\prod\limits_{i=2}^{n} (x+i)$。它的$i$次项系数就是$n-i$种颜色(落脚点)的方案数。
考虑怎么求这个东西。首先最简单粗暴的就是分治$FFT$。时间复杂度$O(nlog^2n)$。可以得到80分。
然而这是很多余的。。。你分治的时候,左边是$\prod\limits_{i=l}^{mid} (x+i)$右边是$\prod\limits_{i=mid+1}^{r} (x+i)$
发现如果项数一样,设前者为$F(x)$那后者就是$F(x+mid-l+1)$。设$u=mid-l+1,F(x)=\sum\limits_{t=0}^{c} a_t x^t$.
然后可以发现有点像二项式定理,化一化式子。
$F(x+u)=\sum\limits_{t=0}^{c} a_t (x+u)^t$.
$=\sum\limits_{t=0}^{c} a_t \sum\limits_{i=0}^{t} \binom{t}{i} x^i u^{t-i}$.
$=\sum\limits_{i=0}^{c} i! x^i \sum\limits_{t=i}^{c} \frac{u^{t-i}}{(t-i)!} t! $
显而易见的卷积形式。递归求解$F(x)$后,只要再做一次卷积就可以得到另一侧的系数。
特别的,如果项数是奇数,那么多出来的一项暴力乘上去就好了。
时间复杂度$T(n)=T(\frac{n}{2})+O(2n \ log \ n)=O(n \ log \ n)$

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define mod 998244353 4 #define S (1<<22) 5 int n,m,len=1,rev[S],r[S],ans[S],t[S],fac[S],inv[S],R[S]; 6 int mo(int x){return x>=mod?x-mod:x;} 7 int qp(int b,int t,int a=1){for(;t;t>>=1,b=1ll*b*b%mod)if(t&1)a=1ll*a*b%mod;return a;} 8 void NTT(int*a,int op=0){ 9 for(int i=0;i<len;++i)if(rev[i]>i)swap(a[rev[i]],a[i]); 10 for(int i=1;i<len;i<<=1)for(int j=0,w=qp(3,(mod-1)/2/i*(op?-1:1)+mod-1);j<len;j+=i<<1)for(int k=j,x,y,t=1;k<j+i;++k,t=1ll*t*w%mod) 11 x=a[k],y=1ll*a[k+i]*t%mod,a[k]=mo(x+y),a[k+i]=mo(x-y+mod); 12 if(op)for(int iv=qp(len,mod-2),i=0;i<len;++i)a[i]=1ll*a[i]*iv%mod; 13 } 14 void solve(int l,int r){ 15 if(l==r){ans[1]=1;ans[0]=2;return;} 16 int md=l+r>>1,Len=r-l+1;if(Len&1)md--; 17 solve(l,md); 18 len=1;while(len<=Len)len<<=1; 19 for(int i=0;i<len;++i)rev[i]=rev[i>>1]>>1|(i&1?len>>1:0); 20 int L=md-l+1;t[0]=1; 21 for(int i=1;i<=L;++i)t[i]=1ll*t[i-1]*L%mod; 22 for(int i=0;i<=L;++i)t[i]=1ll*t[i]*inv[i]%mod,R[i]=ans[i]*1ll*fac[i]%mod; 23 for(int i=L+1;i<len;++i)t[i]=R[i]=0; 24 reverse(t,t+L+2); 25 NTT(R);NTT(t); 26 for(int i=0;i<len;++i)t[i]=1ll*t[i]*R[i]%mod; 27 NTT(t,-1); 28 for(int i=0;i<=L;++i)t[i]=1ll*t[i+L+1]*inv[i]%mod; 29 for(int i=L+1;i<len;++i)t[i]=0; 30 NTT(t);NTT(ans); 31 for(int i=0;i<len;++i)ans[i]=1ll*ans[i]*t[i]%mod; 32 NTT(ans,-1); 33 if(Len&1){t[0]=0; 34 for(int i=0;i<Len;++i)t[i+1]=ans[i],t[i]=(t[i]+1ll*ans[i]*r)%mod; 35 for(int i=0;i<=Len;++i)ans[i]=t[i]; 36 } 37 } 38 int main(){ 39 cin>>n>>m;fac[0]=1; 40 for(int i=1;i<S;++i)fac[i]=1ll*fac[i-1]*i%mod; 41 inv[S-1]=qp(fac[S-1],mod-2); 42 for(int i=S-2;~i;--i)inv[i]=inv[i+1]*(i+1ll)%mod; 43 solve(2,n); 44 int tot=0; 45 for(int k=1;k<=m&&k<=n;++k)tot=(tot+1ll*ans[n-k]*fac[m-1]%mod*inv[k-1]%mod*inv[m-k])%mod; 46 cout<<tot<<endl; 47 }
T2:芬威克树
大意:$k$进制树状数组,单点加时错写成$x+=lowbit(x)$。(如$k=3$时$lowbit(15)=6$而正常的树状数组应该加$3$)。求其错误的输出。$n \le 10^9,m,k \le 2 \times 10^5$
发现错误的加法会使$lowbit$值成环。所有点$x$向$x+lowbit(x)$连边,那么形状会是一棵树。
如果最低位的位次(而不是值)不变,我们称这样的边是重边。
如果只考虑重边的话,最后构造出的是若干链,链首要么指向另一条链,要么指向大于$n$的位置。
这样我们对于重链用数据结构维护,其余暴跳即可。
重链维护的操作是后缀加,单点查。可以转化为单点加,前缀查。这样常数更小,也不再需要懒标记什么的。
若干动态开点线段树解决。下标都是$[1,n]$即可。
现在的问题是给出一个点,需要快速找到它的链首,以便找到对应线段树的根。
考虑倍增。设$st[i][j]$表示数$lowbit$值为$i$,在减法借位了$2^j$后对应的是几。也就是$x=x+lowbit(x)$的逆操作。
举例子:$10$进制下的数$127$。其$lowbit$为$7$,可以借位$\frac{127}{10}=12$次,那就是$st[3][st[2][7]]$。其中$12=2^3+2^2$
而如果要找根的数是进制的整倍数,那么提取出进制数单算就好了。也就是说$12700$找到的就是$100st[3][st[2][7]]$
对于不在链上的点(也就是链首指向并非大于n位置的链),这样的链没有进入循环,故链长不长,是$O(log)$级别的
也就是说,这样的点相较于$k$其实只是$2$的次数不够,$2$的次数够了当前位就会变成$0$从而进入其它链
所以判断一个点是否在链上的依据就是:比较它的$lowbit$和$k$的$2$的次数谁多,如果$k$的多就说明不在链上,暴力跳,否则就去找跟弄线段树就行。
所以暴跳的总次数是$log_k n \ log_2 k$。实际上并不大。
单独再开一个$map$之类的维护原值就好了。
求$lowbit$的复杂度是$O(log)$的
因为$k=2$时跳的次数较多,常数挺大,这时候$lowbit$用位运算比较好,不然可能被卡常。
时间复杂度大概是$O(m \ log \ n \ + \ m \ log_2 k \ log_k \ n)$

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define S 53333333 4 #define s 3333333 5 unordered_map<int,int>M,rt; 6 int lc[S],w[S],rc[S],pc,lcnt,n,p,k,m,iv[29][s],rm[s],crm[s]; 7 int lowbit(int x){if(k==2)return x&-x;int r=1;while(x%k==0)x/=k,r*=k;return x%k*r;} 8 int low(int x){if(k==2)return 1;while(x%k==0)x/=k;return x%k;} 9 void add(int&p,int pos,int v,int cl=1,int cr=n){ 10 if(!p)p=++pc; 11 if(cl==cr)return void(w[p]^=v); 12 if(pos<=cl+cr>>1)add(lc[p],pos,v,cl,cl+cr>>1); 13 else add(rc[p],pos,v,(cl+cr>>1)+1,cr); 14 w[p]=w[lc[p]]^w[rc[p]]; 15 } 16 int ask(int p,int r,int cl=1,int cr=n){ 17 if(!p)return 0; 18 if(cr<=r)return w[p]; 19 return ask(lc[p],r,cl,cl+cr>>1)^(r>cl+cr>>1?ask(rc[p],r,(cl+cr>>1)+1,cr):0); 20 } 21 int find(int x){ 22 int r=rm[low(x)],t=x,c=0;while(t%k==0)t/=k,c++;t/=k; 23 for(int i=28;~i;--i)if(t&1<<i)r=iv[i][r]; 24 while(c--)r*=k;return r; 25 } 26 int main(){ 27 cin>>n>>m>>k;n++; 28 int _=k;while(!(_&1))p++,_>>=1; 29 for(int i=1;i<k;++i)rm[i]=i&1?i:rm[i>>1],crm[i]=i&1?0:crm[i>>1]+1; 30 for(int i=1;i<k;++i)iv[0][i]=rm[rm[i]+_>>1]; 31 for(int i=1;i<29;++i)for(int j=1;j<k;++j)iv[i][j]=iv[i-1][iv[i-1][j]]; 32 for(int $=0,op,x,y;$<m;++$){ 33 scanf("%d%d",&op,&x); 34 if(op^1){ 35 int ans=0; 36 while(x)ans^=crm[low(x)]<p?M[x]:ask(rt[find(x)],x),x-=lowbit(x); 37 printf("%d\n",ans); 38 39 }else{ 40 scanf("%d",&y); 41 while(x<=n&&crm[low(x)]<p)M[x]^=y,x+=lowbit(x); 42 if(k^2)add(rt[find(x)],x,y); 43 } 44 } 45 }
T3:礼物
大意:$n$长的环,选出$m$位置,不得连续超过$k$个相邻的被选中。循环同构,方案数?$T \le 5,l \le m \le n \le 10^6$
循环同构还想不到群论,我大概是个傻子了。
$burnside$直接套。枚举(群论中)环的长度,求的是$\sum\limits_{i|gcd(n,m)} \varphi(i) F(\frac{n}{i},\frac{m}{i})$
$F(n,m)$表示$n$点的环选$m$个相邻不超过$k$个,循环不同构的方案数。
考虑怎么求。首尾相连不超过$k$这个限制挺恶心的,所以我们得钦定点东西让这条限制取消。
我们钦定第一个位置一定不被选,那么剩下的就是序列上的问题了。
枚举有几个超过$k$个的段进行容斥,插板法计算方案,是之前做过的原题了。
然后因为我们钦定了第一个点没有被选,而不被选的点是$n-m$个,在总方案中的占比就是$\frac{n-m}{n}$。所以算出的方案数还要乘$\frac{n}{n-m}$
时间复杂度$O(n \ log \ n)$的。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define mod 998244353 4 #define S 1111111 5 int n,m,k,t,g,ans,fac[S],inv[S]; 6 int gcd(int a,int b){return b?gcd(b,a%b):a;} 7 int qp(int b,int t,int a=1){for(;t;t>>=1,b=1ll*b*b%mod)if(t&1)a=1ll*a*b%mod;return a;} 8 int phi(int x){ 9 int a=x; 10 for(int i=2;i*i<=x;++i)if(x%i==0){ 11 a=a/i*(i-1); 12 while(x%i==0)x/=i; 13 }if(x^1)a=a/x*(x-1);return a; 14 } 15 int C(int b,int t){return b<t||t<0?0:1ll*fac[b]*inv[t]%mod*inv[b-t]%mod;} 16 int cal(int n,int m){n-=m;int a=0;for(int t=0;t*k<=m&&t<=n;++t)a=(a+(t&1?mod-1ll:1ll)*C(m-t*k+n-1,n-1)%mod*C(n,t))%mod;return 1ll*a*(n+m)%mod*qp(n,mod-2)%mod;} 17 int main(){ 18 fac[0]=1;for(int i=1;i<S;++i)fac[i]=1ll*fac[i-1]*i%mod; 19 inv[S-1]=qp(fac[S-1],mod-2); 20 for(int i=S-2;~i;--i)inv[i]=inv[i+1]*(i+1ll)%mod; 21 cin>>t;while(t--){cin>>n>>m>>k;g=gcd(n,m);ans=0;k++; 22 for(int d=1;d*d<=g;++d)if(g%d==0){ 23 ans=(ans+1ll*phi(d)*cal(n/d,m/d))%mod; 24 if(d*d^g)ans=(ans+1ll*phi(g/d)*cal(n*d/g,m*d/g))%mod; 25 }cout<<1ll*ans*qp(n,mod-2)%mod<<endl; 26 } 27 }


