[考试反思]0204省选模拟18:严苛
又是原题。。。又是4个半小时,也就又炸了A
每次考4道题整个人都不知道在干啥反正忙忙活活的4个半小时就过去了想到正解的基本都A不掉就指望着部分分。。。
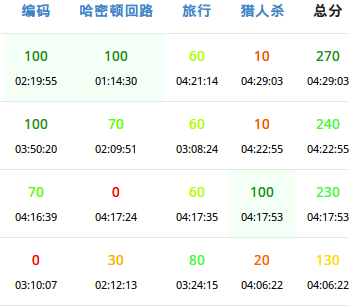
说好听点是rk4。然而这个分差也没啥好说的。后面的都差不多我这个分。
估分是0+30+30+40=100。
T1是原题。离考试结束还有5分钟时突然想起来自己有个地方写的不对,来不及改了。
还是个subtask。那个写伪的东西本来还有一定正确率结果就0了。
T2想到了正解的标签$meet\ in\ middle$然而因为是搜索所以没有细算复杂度,时空复杂度乘了个14再附加巨大常数,TLE+MLE,拿了个暴力分。
(还不如直接写暴力还费了我好长时间也不出个n=11/12什么的来一点梯度。。。)
T3的话考场上想到二分答案,然后不会算状态数所以就乱搞去了,随机化+贪心得了80分。
刚开始还在窃喜分怎么这么高,后来发现我和正解的差别就是正解不随机化而是直接暴力之后我就觉得,啊。。。。
还是不要总想着乱搞了,不一定比暴力好。。。
T4的话时间剩的不多,关键是有一道极其恶心的同名题,题意也有些相似于是这题就没好好想。
最后随便写了个高斯消元+状压想拿40结果没好好看题,输出错东西了丢了20。(剩下20纯粹撞上的n=2俩点。。。)
所以就又这么不明不白的想了仨正解然后炸成130分。。?
也不知道最近自己在干啥。。好像也不是很颓啊。。。反正每天改题倒挺快做题就不行(改题当然快考场上能想到正解就是写不对啊)
也许是不适应4道题4.5h的节奏。不想空题但是又没有对拍的时间。。。(如果一个正解都想不到可能反而没有这样的忧愁。。)
T1:编码
原题。当时的博客貌似也还能看。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define S 6666666 4 char s[S];int fir[S],l[S],to[S],bl[S],n,dfn[S],low[S],tim,sta[S],top,is[S],scc,pc,c[S][2],ec,h[S],rt,tp[S],PC,o[2][S]; 5 vector<int>v[S]; 6 void link(int a,int b){if(a>3&&b>3)l[++ec]=fir[a],fir[a]=ec,to[ec]=b;} 7 void tarjan(int p){ 8 dfn[p]=low[p]=++tim;sta[++top]=p;is[p]=1; 9 for(int i=fir[p];i;i=l[i])if(!dfn[to[i]])tarjan(to[i]),low[p]=min(low[p],low[to[i]]); 10 else if(is[to[i]])low[p]=min(low[p],dfn[to[i]]); 11 if(dfn[p]==low[p]){ 12 scc++; 13 while(is[p])bl[sta[top]]=scc,is[sta[top]]=0,top--; 14 } 15 } 16 void insert(int&p,int al,int o){ 17 if(!p)p=++pc; 18 if(!s[al])return v[p].push_back(o); 19 insert(c[p][s[al]-48],al+1,o); 20 } 21 void dfs(int p,int f){ 22 if(!p)return; 23 for(int i=0,P;i<v[p].size();++i){ 24 P=v[p][i];int x=o[P&1][P>>1],y=o[f&1][f>>1]; 25 link(P<<1|1,x^1),link(P<<1,x^1),link(P<<1,f<<1),link(f<<1|1,P<<1|1); 26 link(x,f<<1);link(y,P<<1|1); 27 f=P; 28 } 29 dfs(c[p][0],f);dfs(c[p][1],f); 30 } 31 int main(){//freopen("1.in","r",stdin); 32 cin>>n;PC=(n<<1|1)<<1|1; 33 for(int i=1;i<=n;++i)o[0][i]=++PC,o[1][i]=++PC; 34 for(int i=1;i<=n;++i){ 35 scanf("%s",s); 36 int qs=S-1; 37 for(int x=0;s[x];++x)if(s[x]=='?')qs=x; 38 s[qs]='0';insert(rt,0,i<<1); 39 s[qs]='1';insert(rt,0,i<<1|1); 40 } 41 dfs(rt,0);for(int i=4;i<=PC;++i)if(!dfn[i])tarjan(i); 42 for(int i=1;i<=n;++i)if(bl[o[0][i]]==bl[o[1][i]])return puts("NO"),0; 43 puts("YES"); 44 }
T2:哈密顿回路
大意:问图中是否存在长为$L$的哈密顿回路。$L \le 10^{13},n \le 14$
14这种数据范围不难想到$meet\ in\ middle$。钦定$n-1$为起点跑出所有长度为$7$的路径和长度为$n-8$的路径合并起来就行。(记录路径终点)
具体实现会卡常,STL只有vector能用剩下都被卡常。$sort$后$two \ pointers$判断答案即可。vector只存长度有用的路径就行不然可能会$MLE$

1 #include<bits/stdc++.h> 2 using namespace std; 3 vector<long long>S[14][1<<13]; 4 long long L,dt[14][14];int n,N,cntb[1<<14],rb[1<<14]; 5 void dfs(int p,int s,long long d){ 6 if(d>L)return; 7 if(cntb[s]==7||cntb[s]==n-8||cntb[s]==n-1)S[p][s].push_back(d); 8 if(cntb[s]==7)return; 9 for(int x=N-1^s,i;i=x&-x,i;x^=i)dfs(rb[i],s|i,d+dt[p][rb[i]]); 10 } 11 int main(){//freopen("1.in","r",stdin); 12 cin>>n>>L;N=1<<n-1; 13 for(int i=0;i<n;++i)for(int j=0;j<n;++j)cin>>dt[i][j]; 14 for(int i=0;i<n;++i)rb[1<<i]=i; 15 for(int i=1;i<N;++i)cntb[i]=cntb[i^i&-i]+1; 16 dfs(n-1,0,0); 17 for(int i=0;i<n;++i)for(int j=0;j<N;++j)sort(S[i][j].begin(),S[i][j].end()),S[i][j].push_back(L+1); 18 if(n<=7){ 19 for(int t=0;t<n-1;++t)if(*lower_bound(S[t][N-1].begin(),S[t][N-1].end(),L-dt[n-1][t])==L-dt[n-1][t])return puts("possible"),0; 20 return puts("impossible"),0; 21 } 22 for(int s=0;s<N;++s)if(cntb[s]==7) 23 for(int j=0;j<n;++j)if(s&1<<j) 24 for(int b=0;b<n;++b)if(!(s&1<<b)){ 25 int pt1=S[b][N-1^s].size()-1; 26 for(int i=0;i<S[j][s].size();++i){ 27 while(S[j][s][i]+S[b][N-1^s][pt1]+dt[b][j]>L)if(pt1)pt1--;else goto F; 28 if(S[j][s][i]+S[b][N-1^s][pt1]+dt[b][j]==L)return puts("possible"),0; 29 }F:; 30 } 31 puts("impossible"); 32 }
T3:旅行
大意:每个点只有$0$或$2$个儿子的边带权树。每条树边只能经过2次。从一个叶节点出发遍历所有叶节点。求相邻两个叶子节点最大距离的最小值。$n \le 200000$
每棵子树都是一进一出。对于有儿子的节点,它要在两个儿子的进出中分别选择一个进行合并更新答案,剩余两个加上边权后上传。
但是这里这个“更新答案”并没有一个明确的界,如果记录所有决策的话状态又太多。
所以考虑二分答案。我们把求解问题又转化成了判定合法。这样的话,合并时我们分情况讨论。
对于每个子树上下两条路径,较大的为a较小的为b。
如果$lc.a+rc.a \geq mid$那么就这么合并并且上传$\{lc.b+w,rc.b+w \}$。$w$为边权。
否则如果$lc.b+rc.b > mid$那么不存在合法配对方案。
否则如果$lc.b+rc.a > mid$且$lc.a+rc.b>mid$那么唯一的配对方案就是$lc.b+rc.b$。上传$\{ lc.a+w,rc.a+w\}$
否则你就有两种方案,a和b合并。
然后如果你像我一样弱智的话你就会想到随机化多做几次看看能不能撞上最优决策。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define S 666666 4 int n,lc[S],rc[S],a[S],b[S],w[S],lim,ok; 5 void dfs(int p){ 6 if(ok*lc[p]==0){a[p]=b[p]=w[p];return;} 7 dfs(lc[p]);dfs(rc[p]); 8 if(a[lc[p]]+a[rc[p]]<=lim)b[p]=b[lc[p]]+w[p],a[p]=b[rc[p]]+w[p]; 9 else if(b[lc[p]]+b[rc[p]]>lim)ok=0; 10 else if(a[lc[p]]+b[rc[p]]>lim&&a[rc[p]]+b[lc[p]]>lim)a[p]=a[lc[p]]+w[p],b[p]=a[rc[p]]+w[p]; 11 else if(a[lc[p]]+b[rc[p]]>lim)a[p]=a[lc[p]]+w[p],b[p]=b[rc[p]]+w[p]; 12 else if(a[rc[p]]+b[lc[p]]>lim)a[p]=a[rc[p]]+w[p],b[p]=b[lc[p]]+w[p]; 13 else if(rand()&1)a[p]=a[lc[p]]+w[p],b[p]=b[rc[p]]+w[p]; 14 else a[p]=a[rc[p]]+w[p],b[p]=b[lc[p]]+w[p];; 15 if(a[p]<b[p])swap(a[p],b[p]); 16 } 17 bool chk(int x){ 18 lim=x; 19 for(int i=1;i<=10;++i){ok=1;dfs(1);if(ok)return 1;} 20 return 0; 21 } 22 int main(){ 23 scanf("%d",&n); 24 for(int i=2,f;i<=n;++i){ 25 scanf("%d%d",&f,&w[i]); 26 if(lc[f])rc[f]=i;else lc[f]=i; 27 } 28 int l=0,r=0x3fffffff,ans; 29 while(l<=r)if(chk(l+r>>1))ans=r=l+r>>1,r--;else l=(l+r>>1)+1; 30 cout<<ans<<endl; 31 }
然而你们都没有我这么弱智。所以直接记录下所有方案就行了。对于两种方案$x,y$如果$x.a \le y.a$且$x.b \le y.b$那么$y$肯定就废了。
删除冗余状态之后状态数小于$n \ log \ n$。所以直接来就行。
然而因为状态数非常少所以没用单调指针。。。然而取出冗余状态之后肯定也构造不出能卡掉的数据。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define S 666666 4 struct P{ 5 int a,b; 6 friend bool operator<(P x,P y){return x.a<y.a||(x.a==y.a&&x.b<y.b);} 7 }; 8 P q(int A,int B){return (P){max(A,B),min(A,B)};} 9 int n,lc[S],rc[S],a[S],b[S],w[S],lim,ok;vector<P>x[S],R; 10 void dfs(int p){ 11 x[p].clear(); 12 if(ok*lc[p]==0){x[p].push_back(q(w[p],w[p]));return;} 13 dfs(lc[p]);dfs(rc[p]); 14 for(int i=0;i<x[lc[p]].size();++i)for(int j=0;j<x[rc[p]].size();++j){ 15 if(x[lc[p]][i].a+x[rc[p]][j].a<=lim)x[p].push_back(q(x[lc[p]][i].b+w[p],x[rc[p]][j].b+w[p])); 16 else if(x[lc[p]][i].a+x[rc[p]][j].b>lim&&x[lc[p]][i].b+x[rc[p]][j].a>lim) 17 {if(x[lc[p]][i].b+x[rc[p]][j].b<=lim)x[p].push_back(q(x[lc[p]][i].a+w[p],x[rc[p]][j].a+w[p]));} 18 else{ 19 if(x[lc[p]][i].a+x[rc[p]][j].b<=lim)x[p].push_back(q(x[lc[p]][i].b+w[p],x[rc[p]][j].a+w[p])); 20 if(x[lc[p]][i].b+x[rc[p]][j].a<=lim)x[p].push_back(q(x[lc[p]][i].a+w[p],x[rc[p]][j].b+w[p])); 21 } 22 } 23 if(x[p].empty()){ok=0;return;} 24 sort(x[p].begin(),x[p].end()); 25 int mnb=x[p][0].b;R.clear(); 26 R.push_back(x[p][0]); 27 for(int i=1;i<x[p].size();++i)if(x[p][i].b<mnb)R.push_back(x[p][i]),mnb=x[p][i].b; 28 swap(R,x[p]); 29 } 30 bool chk(int x){lim=x;ok=1;dfs(1);return ok;} 31 int main(){ 32 scanf("%d",&n); 33 for(int i=2,f;i<=n;++i){ 34 scanf("%d%d",&f,&w[i]); 35 if(lc[f])rc[f]=i;else lc[f]=i; 36 } 37 int l=0,r=0x3fffffff,ans; 38 while(l<=r)if(chk(l+r>>1))ans=r=l+r>>1,r--;else l=(l+r>>1)+1; 39 cout<<ans<<endl; 40 }
T4:猎人杀
大意:上来打(k-1)mod \ 一枪,每个人挨打之后会顺时针数$k$个活人朝他打一枪然后自己$50\%$死亡,求$0$号吃鸡的概率。$n \le 2000$
设$dp[i][j]$表示还有$i$个人现在$j$挨打了的情况下最后$0$号吃鸡的概率。
$dp[i][j]=\frac{dp[i][j+k]+dp[i-1][j-1+k]}{2}$。如果$j=0$则没有第二项。
转移明显分层,但是有环。发现环都是简单环,带入解就行了。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define mod 1000000007 4 #define i2 500000004ll 5 int n,k,f[2222][2222]; 6 int qp(int b,int t,int a=1){for(;t;t>>=1,b=1ll*b*b%mod)if(t&1)a=1ll*a*b%mod;return a;} 7 int main(){ 8 cin>>n>>k;f[1][0]=1; 9 for(int i=2;i<=n;++i){ 10 for(int j=0;j<i;++j)f[i][j]=-1; 11 int x=0,q=1,rt=1,v=-i2*f[i-1][(k-1)%(i-1)]%mod,l; 12 while(q+x)q=0,l=x,x=(l+k)%i,rt=rt*i2%mod,v=(v+1ll*rt*f[i-1][(l+k-1)%(i-1)])%mod; 13 f[i][0]=1ll*v*qp(mod+1-rt,mod-2)%mod; x=(-k%i+i)%i; 14 while(x)f[i][x]=(f[i][(x+k)%i]+f[i-1][(x+k-1)%(i-1)])*i2%mod,x=(x-k%i+i)%i; 15 for(int j=1;j<i;++j)if(f[i][j]==-1){ 16 int x=j,q=1,rt=1,v=0,l; 17 while(q+x!=j)q=0,l=x,x=(l+k)%i,rt=rt*i2%mod,v=(v+1ll*rt*f[i-1][(l+k-1)%(i-1)])%mod; 18 f[i][j]=1ll*v*qp(mod+1-rt,mod-2)%mod; x=((j-k)%i+i)%i; 19 while(x!=j)f[i][x]=(f[i][(x+k)%i]+f[i-1][(x+k-1)%(i-1)])*i2%mod,x=(x-k%i+i)%i; 20 } 21 }cout<<f[n][(k-1)%n]<<endl; 22 }


