[考试反思]0117省选模拟10：争夺

T3出了一点锅，于是按IOI赛制打的。

可能也是这辈子唯一一次好好打的IOI赛制了。

提答，又沉里面了，进去就出不来。莫名的虚荣让我根本没有回头看传统题。

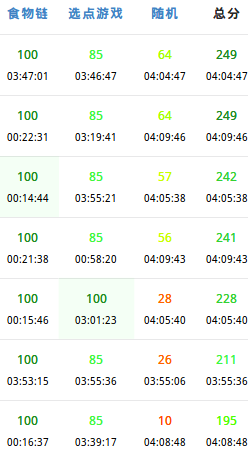
于是的确在T3的80%时间里一直单题rk1，然而其实很慌，剩下两道题又怎样？

运气好，T1特别水，T2数据水，T3用奇技淫巧多拿7分于是并列rk1了。

数组没清空丢了1分。。。

状态差的不行，一下午一道题都没改出来。。。咕到第二天也没改出来

于是在第二天考试的时候写完三个暴力之后终于把T2A了。。。

然后第二天考试就炸了，没什么好说的

 

T1：食物链

大意：就生物上那个。数条数。$n \le 100000,m\le 200000$

当成生物题做就行。拓扑。

#include<bits/stdc++.h>
using namespace std;
#define S 200005
int in[S],out[S],deg[S],l[S],fir[S],to[S],ec,n,m,q[S],t;long long dp[S],ans;
void link(int a,int b){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;in[b]++;out[a]++;}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1,a,b;i<=m;++i)scanf("%d%d",&a,&b),link(a,b);
    for(int i=1;i<=n;++i)if(!in[i])q[++t]=i,dp[i]=1;else deg[i]=in[i];
    for(int h=1;h<=t;++h)for(int i=fir[q[h]];i;i=l[i]){
        dp[to[i]]+=dp[q[h]];deg[to[i]]--;
        if(!deg[to[i]])q[++t]=to[i];
    }
    for(int i=1;i<=n;++i)if(in[i]&&!out[i])ans+=dp[i];
    cout<<ans<<endl;
}

 

T2：选点游戏

大意：支持连边，询问某个联通块中最大独立集。点权为1。保证最后是个树。$n\le 200000,m\le 800000$

维护子树信息的$LCT$。每个$splay$根维护的是一条实链，开四个变量维护这条链的顶端和底端分别选或不选的最优值。

比$ddp$和正解都要好理解，好写一些。。。但是常数巨大。

有一点小的分类讨论，其实代码非常好写。。。$1.6k$

#include<bits/stdc++.h>
using namespace std;
const int S=200005,inf=20040124;
int c[2][S],f[S],s[S],lz[S],dp0[S],dp1[S];
#define lc c[0][p]
#define rc c[1][p]
int Max(int a,int b,int c){return max(max(a,b),c);}
struct V{
    int __,_$,$_,$$;
    V(int a=0,int b=0,int c=0,int d=0){__=a,_$=b;$_=c;$$=d;}
    int val(){return Max(max(__,$_),_$,$$);}
    V operator+(V x){return V(Max(__+x.__,__+x.$_,_$+x.__),Max(__+x._$,__+x.$$,_$+x._$),Max($_+x.__,$_+x.$_,$$+x.__),Max($_+x._$,$$+x._$,$_+x.$$));}
}v[S];
bool nr(int p){return c[0][f[p]]==p||c[1][f[p]]==p;}
void rev(int p){lz[p]^=1,swap(lc,rc),swap(v[p].$_,v[p]._$);}
void up(int p){v[p]=V(dp0[p],-inf,-inf,dp1[p]+1);if(lc)v[p]=v[lc]+v[p];if(rc)v[p]=v[p]+v[rc];}
void down(int p){if(lz[p])rev(lc),rev(rc),lz[p]=0;}
void spin(int p){
    int F=f[p],G=f[F],D=c[1][F]==p,B=c[!D][p];
    if(nr(F))c[c[1][G]==F][G]=p; c[!D][p]=F; c[D][F]=B;
    if(B)f[B]=F; f[f[F]=p]=G; up(F);
}
void splay(int p){
    int tp=1,y=p,F;s[1]=p;
    while(nr(y))s[++tp]=y=f[y]; while(tp)down(s[tp--]);
    for(;F=f[p],nr(p);spin(p))if(nr(F))spin(c[1][F]==p^c[1][f[F]]==F?p:F); up(p);
}
void asas(int r){
    for(int y=0,p=r;p;p=f[y=p]){
        splay(p);
        dp0[p]+=v[rc].val()-v[y].val();
        dp1[p]+=max(v[rc].__,v[rc]._$)-max(v[y].__,v[y]._$);
        rc=y,up(p);
    }splay(r);
}
void make(int p){asas(p);rev(p);}
void link(int x,int y){make(x);make(y);f[x]=y;dp0[y]+=v[x].val();dp1[y]+=max(v[x].__,v[x]._$);}
int main(){//freopen("1.in","r",stdin);
    int n,m;cin>>n>>m;while(m-->0){
        int opt,x,y;scanf("%d",&opt);
        if(opt)scanf("%d%d",&x,&y),link(x,y);
        else scanf("%d",&x),make(x),printf("%d\n",v[x].val());
    }
}

 

T3：随机

大意：看代码求输出的期望。

$Test1:$随机返回$[1,n]$的随机数。

$\frac{1+n}{2}$

#include<bits/stdc++.h>
using namespace std;
const int data[]={1,10,100,1024,10000,20000,50000,100000,524288,1000000};
int main(){
    freopen("random1.out","w",stdout);
    for(int i=0;i<10;++i)printf("%.10Lf\n",(1.0L+data[i])/2);
}

$Test2:$$n$个$[1,1000000]$的随机变量的最小值。

《地震后的幻想乡》的结论，$n$个随机$[0,1]$变量的最小值期望是$\frac{1}{n+1}$

#include<bits/stdc++.h>
using namespace std;
const int data[]={1,10,100,1024,10000,20000,50000,100000,524288,1000000};
int main(){
    freopen("random2.out","w",stdout);
    for(int i=0;i<10;++i){
        __float128 ans=0;
        for(int x=1;x<=1000000;++x){
            ans+=pow(x/1000000.0L,data[i]);
        }printf("%.10Lf\n",(long double)ans);
    }
}

$Test3:$不断在$n$个变量中随机取值，求所有变量都被取过的期望步数。

求取到下一个没取过的变量的期望步数进行累加。

#include<bits/stdc++.h>
using namespace std;
const int data[]={1,10,100,1024,10000,20000,50000,100000,524288,1000000};
int sta[11111];
int main(){
    freopen("random3.out","w",stdout);
    for(int i=0;i<10;++i){
        __float128 ans=0;
        for(int j=1;j<=data[i];++j)ans+=1.0L/j;
        printf("%.10Lf\n",(long double)(ans*data[i]));
    }
}

$Test4:$不断在$n$个变量中随机取值，求某一个变量被取过两次的期望步数。

枚举步数，计算概率进行累加，概率很好算是个前缀积。

#include<bits/stdc++.h>
using namespace std;
const int data[]={1,10,100,1024,10000,20000,50000,100000,524288,1000000};
int main(){
    freopen("random4.out","w",stdout);
    for(int i=0;i<=9;++i){
        __float128 pre=1,ans=0;
        for(int t=1;t<=data[i];++t){
            ans+=pre*t/data[i]*(t+1);
            pre*=((__float128)data[i]-t+0.0L)/data[i];
        }printf("%.10Lf\n",(long double)ans);
    }
}

$Test5:$求线段树区间询问时期望涉及多少个节点。

考虑每个节点会在多少个方案中出现，当且仅当询问区间与当前节点区间相交且不包含父节点的完整区间。

#include<bits/stdc++.h>
using namespace std;
const int data[]={1,10,100,1024,10000,20000,50000,100000,524288,1000000};
__float128 ans,all;int I;
void build(int l,int r,int fl,int fr){
    int lp=l-1,rp=data[I]-r;
    ans+=all-(lp+1.0L)*lp/2-(rp+1.0L)*rp/2-1.0L*fl*(data[I]-fr+1);
    if(l==r)return;
    build(l,l+r>>1,l,r);build((l+r>>1)+1,r,l,r);
}
int main(){
    freopen("random5.out","w",stdout);
    for(int i=0;i<=9;++i){I=i;
        ans=0;all=(data[i]+1.0L)*data[i]/2;build(1,data[i],0,-1);
        printf("%.10Lf\n",(long double)(ans/all));
    }
}

$Test6:$求$Treap$期望深度和。

考虑加入一个节点的贡献，设$dp[n]$为$n$个节点的树的答案，那么$dp[n]=\frac{\sum\limits_{i=1}^{n} dp[i-1]+dp[n-i]}{n}$。

上边那个就是一个前缀和。

#include<bits/stdc++.h>
using namespace std;
long double dp[1000005],pre[1000005];
const int data[]={1,10,100,1024,10000,20000,50000,100000,524288,1000000};
int main(){
    freopen("random6.out","w",stdout);
    dp[1]=pre[1]=1;
    for(int i=2;i<=data[9];++i)dp[i]=2*pre[i-1]/i+i,pre[i]=pre[i-1]+dp[i];
    for(int i=0;i<=9;++i)printf("%.10Lf\n",dp[data[i]]);
}

$Test7:$不会。

$Test8:$不断在$n$个变量中随机取值，不会取到已经取过的，取到时它的所有倍数也被取到。求所有变量都被取过的期望步数。

每个节点被取到之可能是它的某个约数被取到，概率是均等的，所以答案是$\sum\limits_{i=1}^{n} \frac{1}{d(i)}$

#include<bits/stdc++.h>
using namespace std;
const int data[]={1,10,100,1024,10000,20000,50000,100000,524288,1000000};
__float128 ans;int I;
int main(){
    freopen("random8.out","w",stdout);
    for(int i=0;i<=9;++i){
        ans=0;
        for(int x=1;x<=data[i];++x){
            int cnt=0;
            for(int y=1;y*y<=x;++y)if(x%y==0){
                cnt++;if(y*y!=x)cnt++;
            }
            ans+=1.0L/cnt;
        }
        printf("%.10Lf\n",(long double)ans);
    }
}

$Test9:$值域为$10$，长度为$n$的随机序列的期望$LIS$。

当$n$很大时答案直接近似成$10$。小点十进制压状态记搜$0.05s$都跑不到。

$LIS$的转移只与前面每个值对应的最大$dp$值有关，压起来就搜就行了，实际上$1000$的点都跑不到$0.5s$

#include<bits/stdc++.h>
using namespace std;
const int data[]={1,10,100,1024,10000,20000,50000,100000,524288,1000000};
unordered_map<int,long double>M[101];
int I,a[11],dp[11];long long ans,tms;
int r[101][11],rr[101][11];
long double sch100(int stp,int st){
    if(M[stp].find(st)!=M[stp].end())return M[stp][st];
    if(stp>6)cerr<<stp<<' '<<st<<endl;
    if(!stp)return st%10;int rst=st;
    for(int i=10;i;--i)r[stp][i]=st%10,st/=10;
    long double tot=0;
    for(int c=1;c<=10;++c){
        for(int i=1;i<=10;++i)rr[stp][i]=r[stp][i];
        rr[stp][c]=max(rr[stp][c],rr[stp][c-1]+1);
        if(c==10&&rr[stp][10]==10){tot+=1;break;}
        for(int s=c+1;s<=10;++s)rr[stp][s]=max(rr[stp][s],rr[stp][s-1]);
        register int nst=0;
        for(int i=1;i<=10;++i)nst=(nst<<3)+(nst<<1)+rr[stp][i];
        tot+=0.1*sch100(stp-1,nst);
    }return M[stp][rst]=tot;
}
int main(){
    freopen("random9.out","w",stdout);
    printf("%.10Lf\n",sch100(100,0));
}

$Test10:$不会。