[专题总结]网络流初步(1)
总算A穿第一个专题。来屯思路的。
蜥蜴
没有比这个更板子的了。对于每个石柱拆点成两个,连边限制流量。

1 #include<bits/stdc++.h> 2 using namespace std; 3 int cnt=2,in[22][22],out[22][22],n,m,d,tms[22][22],ecnt=1,dep[1005]; 4 int fir[1005],l[50005],to[50005],v[50005],x,maxflow,q[1005],t,cntt; 5 int fab(int p){return p*p;} 6 void connect(int a,int b,int vv){ 7 l[++ecnt]=fir[a];fir[a]=ecnt;to[ecnt]=b;v[ecnt]=vv; 8 l[++ecnt]=fir[b];fir[b]=ecnt;to[ecnt]=a; 9 } 10 int read1(){ 11 register int ch=getchar(); 12 while(ch<'0'||ch>'3')ch=getchar(); 13 return ch-48; 14 } 15 int read2(){ 16 register int ch=getchar(); 17 while(ch!='L'&&ch!='.')ch=getchar(); 18 return ch=='L'; 19 } 20 int bfs(){ 21 memset(dep,0,sizeof(dep)); dep[1]=q[1]=1; t=1; 22 for(int h=1;h<=t;++h) for(int i=fir[q[h]];i;i=l[i]) 23 if(!dep[to[i]]&&v[i]){ 24 dep[to[i]]=dep[q[h]]+1; 25 q[++t]=to[i]; 26 if(to[i]==2)return 1; 27 } 28 return 0; 29 } 30 int dfs(int p,int flow){ 31 if(p==2)return flow;int res=flow; 32 for(int i=fir[p];i;i=l[i]) if(dep[to[i]]==dep[p]+1&&v[i]&&res){ 33 int q=dfs(to[i],min(res,v[i])); 34 if(!q)dep[to[i]]=0; 35 res-=q;v[i]-=q;v[i^1]+=q; 36 } 37 return flow-res; 38 } 39 int main(){ 40 scanf("%d%d%d",&n,&m,&d); 41 for(int i=1;i<=n;++i) for(int j=1;j<=m;++j){ 42 tms[i][j]=read1(); 43 if(tms[i][j]) connect(cnt+1,cnt+2,tms[i][j]), 44 in[i][j]=++cnt,out[i][j]=++cnt; 45 } 46 for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) 47 if(read2()) connect(1,in[i][j],1),cntt++; 48 for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) if(tms[i][j]) 49 for(int k=1;k<=n;++k) for(int l=1;l<=m;++l) if(tms[k][l]) 50 if(i!=k||j!=l) if(fab(i-k)+fab(j-l)<=fab(d)) 51 connect(out[i][j],in[k][l],1234567); 52 for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) if(tms[i][j]) 53 if(i<=d||n-i<d||j<=d||m-j<d) connect(out[i][j],2,7654321); 54 while(bfs())maxflow+=dfs(1,1234567); 55 printf("%d",cntt-maxflow); 56 }
星际战争
二分答案+最大流。检查是否满流即可。

1 #include<bits/stdc++.h> 2 using namespace std; 3 int ecnt,cnt,atk[55],def[55],can[55][55],fir[123],l[12345],to[12345]; 4 int totd,dep[123],q[123],t,n,m; 5 double max_flow,v[12345]; 6 #define eps 1e-6 7 void connect(int a,int b,double vv){ 8 l[++ecnt]=fir[a];fir[a]=ecnt;to[ecnt]=b;v[ecnt]=vv; 9 l[++ecnt]=fir[b];fir[b]=ecnt;to[ecnt]=a;v[ecnt]=0; 10 } 11 int bfs(){ 12 memset(dep,0,sizeof(dep));dep[1]=q[1]=t=1; 13 for(int h=1;h<=t;++h) for(int i=fir[q[h]];i;i=l[i]) 14 if(!dep[to[i]]&&v[i]>eps){ 15 q[++t]=to[i]; dep[to[i]]=dep[q[h]]+1; 16 if(to[i]==2)return 1; 17 } 18 return 0; 19 } 20 double dfs(int p,double flow){ 21 if(p==2)return flow;double res=flow; 22 for(int i=fir[p];i;i=l[i]) if(dep[to[i]]==dep[p]+1&&v[i]>eps&&res>eps){ 23 double succ=dfs(to[i],min(res,v[i])); 24 if(succ<eps)dep[to[i]]=0; 25 res-=succ;v[i]-=succ;v[i^1]+=succ; 26 } 27 return flow-res; 28 } 29 int main(){ 30 scanf("%d%d",&n,&m); 31 for(int i=1;i<=n;++i) scanf("%d",&def[i]),totd+=def[i]; 32 for(int i=1;i<=m;++i) scanf("%d",&atk[i]); 33 for(int i=1;i<=m;++i) for(int j=1;j<=n;++j) scanf("%d",&can[i][j]); 34 double l=0,r=100000,mid; 35 while(r-l>eps){ 36 mid=(l+r)/2;ecnt=1;max_flow=0; 37 memset(fir,0,sizeof(fir)); 38 for(int i=1;i<=m;++i) connect(1,2+i,mid*atk[i]); 39 for(int i=1;i<=n;++i) connect(2+n+i,2,def[i]); 40 for(int i=1;i<=m;++i) for(int j=1;j<=n;++j) if(can[i][j]) connect(2+i,2+n+j,1e9); 41 while(bfs())max_flow+=dfs(1,1e9); 42 if(totd-max_flow<eps)r=mid; else l=mid; 43 } 44 printf("%.5lf\n",l); 45 }
网络吞吐量
最短路。找出所有最短路上的边,然后还是拆点限制流量。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define inf 0x3f3f3f3f3f3f3f3f 4 #define int long long 5 priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >que; 6 int x[505][505],n,m,fir[1234],l[555555],to[555555],v[555555],ecnt=1; 7 int q[1234],t,dt[555],xx,max_flow,dep[1234]; 8 int _fir[1234],_l[555555],_to[555555],_v[555555],_ecnt=1; 9 void con(int a,int b,int vv){ 10 l[++ecnt]=fir[a];fir[a]=ecnt;to[ecnt]=b;v[ecnt]=vv; 11 l[++ecnt]=fir[b];fir[b]=ecnt;to[ecnt]=a;v[ecnt]=vv; 12 } 13 void _con(int a,int b,int vv){ 14 _l[++_ecnt]=_fir[a];_fir[a]=_ecnt;_to[_ecnt]=b;_v[_ecnt]=vv; 15 _l[++_ecnt]=_fir[b];_fir[b]=_ecnt;_to[_ecnt]=a; 16 } 17 int bfs(){ 18 memset(dep,0,sizeof dep);t=dep[q[1]=3]=1; 19 for(int h=1;h<=t;++h) for(int i=_fir[q[h]];i;i=_l[i]) if(_v[i]&&!dep[_to[i]]){ 20 dep[_to[i]]=dep[q[h]]+1;q[++t]=_to[i]; 21 if(_to[i]==n<<1)return 1; 22 } 23 return 0; 24 } 25 int dfs(int p,int flow){ 26 if(p==n<<1)return flow;int res=flow; 27 for(int i=_fir[p];i;i=_l[i])if(res&&_v[i]&&dep[_to[i]]==dep[p]+1){ 28 int q=dfs(_to[i],min(res,_v[i])); 29 if(!q)dep[_to[i]]=0; 30 res-=q;_v[i]-=q;_v[i^1]+=q; 31 } 32 return flow-res; 33 } 34 signed main(){ 35 scanf("%lld%lld",&n,&m);memset(x,0x3f,sizeof x);memset(dt,0x3f,sizeof dt); 36 for(int i=1,a,b,vx;i<=m;++i)scanf("%lld%lld%lld",&a,&b,&vx),x[a][b]=x[b][a]=min(x[a][b],vx); 37 for(int i=1;i<=n;++i) for(int j=i+1;j<=n;++j) if(x[i][j]!=inf) con(i,j,x[i][j]); 38 que.push(make_pair(0,1));dt[1]=0; 39 while(!que.empty()){ 40 int d=que.top().first,p=que.top().second;que.pop(); 41 if(p==n)break;if(d!=dt[p])continue; 42 for(int i=fir[p];i;i=l[i]) 43 if(dt[to[i]]>d+v[i])dt[to[i]]=d+v[i],que.push(make_pair(dt[to[i]],to[i])); 44 } 45 for(int i=1;i<n;++i)scanf("%lld",&xx),_con(i<<1,i<<1|1,xx); 46 for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) if(dt[i]==dt[j]+x[i][j]) _con(j<<1|1,i<<1,inf); 47 while(bfs())max_flow+=dfs(3,inf); 48 printf("%lld\n",max_flow); 49 }
奇怪的游戏
大型分类讨论。棋盘黑白染色。
如果总位置数是偶数,而黑白格子之和不同,无解。
如果黑白和一样,那么二分答案+网络流check。二分的是最后棋盘上都相同的数字是几。答案满足单调性。
如果你能制造出一种局面使棋盘上都是x,那么因为一共偶数个格子,两两配对+1就可以让他们全是x+1。
如果总位置数是奇数,那么如果有解,最终的值也是确定的,解方程。如一共有x个黑格子和x+1个白格子,每次操作黑白都+1。
那么就是$sum_{black}+x==sum_{white}+x+1$。用上面二分答案里的check去看一下x这个值是否合法就行了。
打着挺麻烦的。网络流要根据格子的黑白来分成二分图再跑。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define int long long 4 #define inf 1234567890123450ll 5 int n,m,T,x[42][42],tot[2],r[42][42],cnt,mx; 6 int ecnt,fir[2222],l[12345],to[12345],v[12345],q[2222],t,dep[2222]; 7 void connect(int a,int b,int vv){//printf("%lld %lld %lld\n",a,b,vv); 8 l[++ecnt]=fir[a];fir[a]=ecnt;to[ecnt]=b;v[ecnt]=vv; 9 l[++ecnt]=fir[b];fir[b]=ecnt;to[ecnt]=a;v[ecnt]=0; 10 } 11 int bfs(){ 12 memset(dep,0,sizeof dep); 13 q[1]=t=dep[1]=1; 14 for(int h=1;h<=t;++h) 15 for(int i=fir[q[h]];i;i=l[i]) 16 if(!dep[to[i]]&&v[i]) 17 dep[to[i]]=dep[q[h]]+1,q[++t]=to[i]; 18 return dep[2]; 19 } 20 int dfs(int p,int flow){ 21 if(p==2)return flow;int res=flow; 22 for(int i=fir[p];i;i=l[i]) 23 if(dep[to[i]]==dep[p]+1&&v[i]&&res){ 24 int q=dfs(to[i],min(res,v[i])); 25 if(!q)dep[to[i]]=0; 26 res-=q;v[i]-=q;v[i^1]+=q; 27 } 28 return flow-res; 29 } 30 bool check(int xx){ 31 memset(fir,0,sizeof fir); 32 ecnt=1;int max_flow=0,in=0; 33 for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) 34 if(i+j&1) connect(1,r[i][j],xx-x[i][j]),in+=xx-x[i][j]; 35 else connect(r[i][j],2,xx-x[i][j]); 36 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)if(i+j&1){ 37 if(i!=1)connect(r[i][j],r[i-1][j],inf); 38 if(i!=n)connect(r[i][j],r[i+1][j],inf); 39 if(j!=1)connect(r[i][j],r[i][j-1],inf); 40 if(j!=m)connect(r[i][j],r[i][j+1],inf); 41 } 42 while(bfs()) max_flow+=dfs(1,inf); 43 return in==max_flow; 44 } 45 signed main(){ 46 // freopen("game1.in","r",stdin); 47 scanf("%lld",&T); 48 while(T--){ 49 scanf("%lld%lld",&n,&m); tot[0]=tot[1]=mx=0; cnt=2; 50 for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) 51 scanf("%lld",&x[i][j]),tot[i+j&1]+=x[i][j],mx=max(mx,x[i][j]),r[i][j]=++cnt; 52 if(n*m&1){ 53 if(mx>tot[0]-tot[1])puts("-1"); 54 else if(check(tot[0]-tot[1])) printf("%lld\n",(tot[0]-tot[1])*m*n-tot[0]-tot[1]>>1); 55 else puts("-1"); 56 }else if(tot[0]!=tot[1])puts("-1"); 57 else{ 58 int l=mx,r=inf; 59 while(l<r-1) 60 if(check(l+r>>1))r=l+r>>1; 61 else l=(l+r>>1)+1; 62 if(check(l))printf("%lld\n",l*n*m-tot[0]-tot[1]>>1); 63 else printf("%lld\n",r*n*m-tot[0]-tot[1]>>1); 64 } 65 } 66 }
土兵占领
我写过题解。。。
紧急疏散evacuate
容易想到二分时间,每一个门都限制mid的流量,加一个最短路,距离小于时间的就连边,看是否能流满。
但是这是不对的。如果有两个人距离门都是2,而二分的时间也是2,判定为有解实际为无解。
具体数据我忘了,大概是这个意思。WA92。
另一个常用思想,还是拆点,不过是根据含义拆点。
把每一个们拆成mid个。表示这扇门在时间t时逃出的机会。那么流向汇点的流量就是1。
然后在每扇门的t到t+1连边,表示现在有人出去了的话就再等1单位时间。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define S 16666666 4 const int dx[]={1,-1,0,0},dy[]={0,0,1,-1}; 5 #define tx x+dx[i] 6 #define ty y+dy[i] 7 int fir[S],l[S],to[S],v[S],q[S],dep[S],n,m,E,cntp,cntd,dt[444][22][22]; 8 char s[22][22];int pc,ec,nord[444][444]; 9 void DFS(int fd,int x,int y,int stp){ 10 dt[fd][x][y]=stp; 11 for(int i=0;i<4;++i)if(dt[fd][tx][ty]>stp+1&&s[tx][ty]=='.')DFS(fd,tx,ty,stp+1); 12 } 13 void link(int a,int b,int V){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;v[ec]=V;} 14 void con(int a,int b,int V){link(a,b,V);link(b,a,0);} 15 bool bfs(){ 16 for(int i=1;i<=E;++i)dep[i]=0; 17 for(int h=1,t=1;h<=t;++h)for(int i=fir[q[h]];i;i=l[i])if(!dep[to[i]]&&v[i]) 18 dep[q[++t]=to[i]]=dep[q[h]]+1; 19 return dep[E]; 20 } 21 int dfs(int p,int flow){int r=flow; 22 if(p==E)return flow; 23 for(int i=fir[p];i;i=l[i])if(dep[to[i]]==dep[p]+1&&v[i]&&r){ 24 int x=dfs(to[i],min(r,v[i])); 25 if(!x)dep[to[i]]=0; 26 v[i]-=x;v[i^1]+=x;r-=x; 27 }return flow-r; 28 } 29 bool chk(int T){ 30 pc=0;ec=1;E=cntd*T+cntp+1; 31 for(int i=1;i<=cntd;++i)for(int j=1;j<=T;++j)nord[i][j]=++pc,con(pc,E,1); 32 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)if(s[i][j]=='.'){ 33 con(0,++pc,1); 34 for(int k=1;k<=cntd;++k)if(dt[k][i][j]<=T)con(pc,nord[k][dt[k][i][j]],1); 35 } 36 for(int i=1;i<=cntd;++i)for(int j=1;j<T;++j)con(nord[i][j],nord[i][j+1],444); 37 int maxflow=0;while(bfs())maxflow+=dfs(0,444); 38 for(int i=0;i<=E;++i)fir[i]=0; 39 return maxflow==cntp; 40 } 41 main(){dep[0]=1; 42 scanf("%d%d",&n,&m);for(int i=1;i<=n;++i)scanf("%s",s[i]+1); 43 memset(dt,0x3f,sizeof dt); 44 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j) 45 if(s[i][j]=='.')cntp++;else if(s[i][j]=='D')DFS(++cntd,i,j,0); 46 int l=0,r=n*m+1,ans=n*m+1; 47 while(l<=r)if(chk(l+r>>1))ans=r=l+r>>1,r--;else l=(l+r>>1)+1; 48 if(ans==n*m+1)return puts("impossible"),0;printf("%d\n",ans); 49 }
狼抓兔子
注意是双向边。
暴力建图跑最小割没什么问题。但是其实复杂度是不对的。
对付这一类问题有一个特殊方法:
适用条件:图可以花在二维平面(纸)上,而且所有边之间的交点都是原图中的结点。这样的话这种图就可以转化为对偶图。
在满足上述条件的图里,二维平面被边分割成了若干多边形。
假设源点S在图的左上角,汇点T在右下角。再连一条inf边从S指向T(从整个图的外围画一个大半圆),会把这个图的外部也分成两部分。简称内部和外部。
把平面上的多边形看作新图的节点(包括被inf边隔开的“内部”与“外部”),建边,边权就是两个多边形之间的公共边的边权。
现在我们求出一条从内部到外部的最短路,它的长度就是最小割。
从含义上理解,你所经过的路径上的边,就是原图中要被割掉的边。要最小,那么就是最短路。

1 #include<cstdio> 2 #include<iostream> 3 using namespace std; 4 #define S 1000005 5 int fir[S],l[S*6],to[S*6],v[S*6],q[S],n,m,o[1005][1005],ec=1,pc,dep[S],ans; 6 void link(int a,int b,int V){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;v[ec]=V;} 7 bool bfs(){ 8 for(int i=1;i<=pc;++i)dep[i]=0;dep[1]=q[1]=1; 9 for(int h=1,t=1;h<=t;++h)for(int i=fir[q[h]];i;i=l[i])if(!dep[to[i]]&&v[i]) 10 dep[q[++t]=to[i]]=dep[q[h]]+1; 11 return dep[pc]; 12 } 13 int dfs(int p,int flow){ 14 if(p==pc)return flow;int r=flow; 15 for(int i=fir[p];i;i=l[i])if(dep[to[i]]==dep[p]+1&&v[i]&&r){ 16 int M=dfs(to[i],min(v[i],r)); 17 if(!M)dep[to[i]]=0; 18 r-=M;v[i]-=M;v[i^1]+=M; 19 }return flow-r; 20 } 21 main(){ 22 scanf("%d%d",&n,&m); for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)o[i][j]=++pc; 23 for(int i=1;i<=n;++i)for(int j=1,x;j<m;++j)scanf("%d",&x),link(o[i][j],o[i][j+1],x),link(o[i][j+1],o[i][j],x); 24 for(int i=1;i<n;++i)for(int j=1,x;j<=m;++j)scanf("%d",&x),link(o[i][j],o[i+1][j],x),link(o[i+1][j],o[i][j],x); 25 for(int i=1;i<n;++i)for(int j=1,x;j<m;++j)scanf("%d",&x),link(o[i][j],o[i+1][j+1],x),link(o[i+1][j+1],o[i][j],x); 26 while(bfs())ans+=dfs(1,0x3fffffff);printf("%d\n",ans); 27 }
切糕
自己想了八百年系列。挺难的。险些颓题解。
最小代价,那么看着像是一个最小割了。
对于每一个纵轴,在上面你会且仅会取一个点,为了表示这种“或”的关系。我们把所有在同一条纵轴上的点“串联”起来。
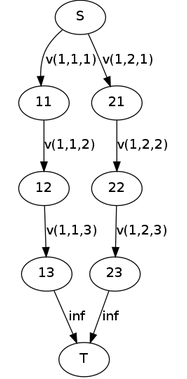
而相邻格子是有限制的,距离不超过D。即选了(i,j,f(i,j))就必须选(i,j+1,[f(i,j)-D,f(i,j)+D])。为了表示这种“且“的关系,将其并联。
注意到这里限制的区间是连续的一段,所以就像物理的什么导线上的试触法一样,把限制的那一段”接入电路”
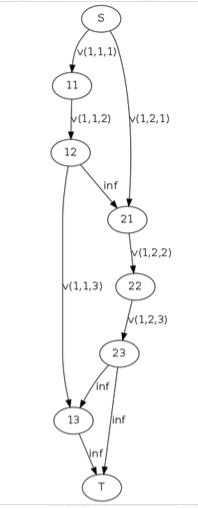
图中以“选了(1,1,3)就必须选(1,2,2~3)”为例。如果你割了v(1,1,3)这条边而不割断v(1,2,2),v(1,2,3)之一的话,那么“电流”就会绕着这条路走向终点,不满足最小割。
所以这样就限制住了“割掉这个边,那么就必须割掉另一条纵轴上连续的区间之一”这种条件。

1 #include<cstdio> 2 #include<iostream> 3 using namespace std; 4 #define rep() for(int i=1;i<=x;++i)for(int j=1;j<=y;++j) 5 #define I 0x3fffffff 6 int w[44][44][44],o[44][44][44],ec=1,pc,fir[66666],l[333333],to[333333],v[333333]; 7 int x,y,z,D,T,ans,q[66666],d[66666]; 8 void link(int a,int b,int V){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;v[ec]=V;} 9 void con(int a,int b,int V){link(a,b,V);link(b,a,0);} 10 int up(int x){return max(x,0);} 11 int down(int x){return min(x,z);} 12 bool bfs(){ 13 for(int i=1;i<=T;++i)d[i]=0; 14 for(int h=1,t=1;h<=t;++h)for(int i=fir[q[h]];i;i=l[i])if(v[i]&&!d[to[i]]) 15 d[q[++t]=to[i]]=d[q[h]]+1; 16 return d[T]; 17 } 18 int dfs(int p,int flow){ 19 if(p==T)return flow;int r=flow; 20 for(int i=fir[p];i;i=l[i])if(v[i]&&r&&d[to[i]]==d[p]+1){ 21 int x=dfs(to[i],min(v[i],r)); 22 if(!x)d[to[i]]=0; 23 v[i]-=x;v[i^1]+=x;r-=x; 24 }return flow-r; 25 } 26 int main(){ 27 scanf("%d%d%d%d",&x,&y,&z,&D);d[0]=1; 28 for(int k=1;k<=z;++k)rep()scanf("%d",&w[i][j][k]); 29 rep()for(int k=0;k<=z;++k)o[i][j][k]=++pc;T=++pc; 30 rep()con(0,o[i][j][0],I),con(o[i][j][z],T,I); 31 rep()for(int k=1;k<=z;++k)con(o[i][j][k-1],o[i][j][k],w[i][j][k]); 32 for(int i=1;i<x;++i)for(int j=1;j<=y;++j)for(int k=1;k<=z;++k) 33 con(o[i][j][k-1],o[i+1][j][up(k-D-1)],I),con(o[i+1][j][down(k+D)],o[i][j][k],I); 34 for(int i=1;i<=x;++i)for(int j=1;j<y;++j)for(int k=1;k<=z;++k) 35 con(o[i][j][k-1],o[i][j+1][up(k-D-1)],I),con(o[i][j+1][down(k+D)],o[i][j][k],I); 36 while(bfs())ans+=dfs(0,I);printf("%d\n",ans); 37 }
Figure Eight
反正不是网络流。。。瞎写。。。

1 #include<cstdio> 2 #include<iostream> 3 using namespace std; 4 #define e 333 5 char c[e][e];int s[e][e],n,mxsz[e][e][e];long long ans;short u[e][e][e],d[e][e][e]; 6 bool ask(int x,int l,int r){return s[x][r]-s[x-1][r]-s[x][l-1]+s[x-1][l-1]==r-l+1;} 7 int main(){ 8 scanf("%d",&n); 9 for(int i=1;i<=n;++i)scanf("%s",c[i]+1); 10 for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+(c[i][j]=='.'); 11 for(int l=1;l<=n;++l)for(int r=l+2;r<=n;++r){ 12 int lst=0; 13 for(int i=1;i<=n;++i) 14 if(ask(i,l,r)){if(lst)u[i][l][r]=i-lst-1;else lst=i;} 15 else if(c[i][l]=='*'||c[i][r]=='*')lst=0; 16 } 17 for(int len=2;len<=n;++len)for(int l=1,r=l+len;r<=n;++l,++r)for(int i=1;i<=n;++i) 18 mxsz[i][l][r]=max(max(mxsz[i][l+1][r],mxsz[i][l][r-1]),u[i][l][r]?(u[i][l][r]*(r-l-1)):0); 19 for(int l=1;l<=n;++l)for(int r=l+2;r<=n;++r){ 20 int lst=0; 21 for(int i=n;i;--i) 22 if(ask(i,l,r)){if(lst)ans=max(ans,(lst-i-1)*(r-l-1ll)*mxsz[i][l][r]);else lst=i;} 23 else if(c[i][l]=='*'||c[i][r]=='*')lst=0; 24 } 25 printf("%lld\n",ans?ans:-1); 26 }
最大获利
最常用的最小割模型之一:选点付出一定代价,两个点同时选获得一定收益。

网上有人管这个叫做三叉戟模型。我觉得不错。
上来把所有可能的收益都累加答案。然后求最小割的含义就是:
要么你同时付出A1,A2的代价(都买下来),否则你就会割舍W(1,2)的收益(没都买下来的话就不会获得收益)

1 #include<cstdio> 2 #include<iostream> 3 using namespace std; 4 #define S 3000005 5 #define M 100000000 6 int fir[S],l[S],to[S],ec=1,v[S],n,m,ans,dep[S],q[S]; 7 void link(int a,int b,int V){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;v[ec]=V;} 8 void con(int a,int b,int V){link(a,b,V);link(b,a,0);} 9 bool bfs(){ 10 for(int i=1;i<=n+m+1;++i)dep[i]=0; 11 for(int h=1,t=1;h<=t;++h)for(int i=fir[q[h]];i;i=l[i])if(v[i]&&!dep[to[i]]) 12 dep[q[++t]=to[i]]=dep[q[h]]+1; 13 return dep[n+m+1]; 14 } 15 int dfs(int p,int flow){ 16 if(p==n+m+1)return flow;int r=flow; 17 for(int i=fir[p];i;i=l[i])if(v[i]&&dep[to[i]]==dep[p]+1&&r){ 18 int x=dfs(to[i],min(r,v[i])); 19 if(!x)dep[to[i]]=0; 20 v[i]-=x;v[i^1]+=x;r-=x; 21 }return flow-r; 22 } 23 int main(){ 24 scanf("%d%d",&n,&m);dep[0]=1; 25 for(int i=1,x;i<=n;++i)scanf("%d",&x),con(0,i,x); 26 for(int i=1,a,b,c;i<=m;++i)scanf("%d%d%d",&a,&b,&c),ans+=c,con(a,i+n,M),con(b,i+n,M),con(i+n,m+n+1,c); 27 while(bfs())ans-=dfs(0,M);printf("%d\n",ans); 28 }
happiness
两个三叉戟完事。
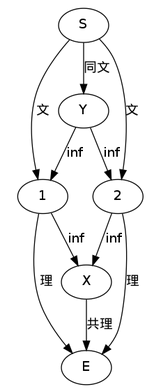
“文-文-X-共理”是一个三叉戟。“理-理-Y-同文”是另一个。含义不难理解。

1 #include<cstdio> 2 #define S 3000005 3 #define M 100000000 4 int n,m,fir[S],l[S],to[S],v[S],o[101][101],pc,ec=1,ans,E,q[S],dep[S]; 5 int min(int a,int b){return a<b?a:b;} 6 void link(int a,int b,int V){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;v[ec]=V;} 7 void con(int a,int b,int V){link(a,b,V);link(b,a,0);} 8 bool bfs(){ 9 for(int i=1;i<=pc;++i)dep[i]=0; 10 for(int h=1,t=1;h<=t;++h)for(int i=fir[q[h]];i;i=l[i])if(!dep[to[i]]&&v[i]) 11 dep[q[++t]=to[i]]=dep[q[h]]+1; 12 return dep[E]; 13 } 14 int dfs(int p,int flow){ 15 if(p==E)return flow;int r=flow; 16 for(int i=fir[p];i;i=l[i])if(r&&v[i]&&dep[to[i]]==dep[p]+1){ 17 int x=dfs(to[i],min(v[i],r)); 18 if(!x)dep[to[i]]=0; 19 v[i]-=x;v[i^1]+=x;r-=x; 20 }return flow-r; 21 } 22 main(){dep[0]=1; 23 scanf("%d%d",&n,&m); for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)o[i][j]=++pc;E=++pc; 24 for(int i=1;i<=n;++i)for(int j=1,x;j<=m;++j)scanf("%d",&x),con(o[i][j],E,x),ans+=x; 25 for(int i=1;i<=n;++i)for(int j=1,x;j<=m;++j)scanf("%d",&x),con(0,o[i][j],x),ans+=x; 26 for(int i=1;i<n;++i)for(int j=1,x;j<=m;++j)scanf("%d",&x),con(o[i][j],++pc,M),con(o[i+1][j],pc,M),con(pc,E,x),ans+=x; 27 for(int i=1;i<n;++i)for(int j=1,x;j<=m;++j)scanf("%d",&x),con(++pc,o[i][j],M),con(pc,o[i+1][j],M),con(0,pc,x),ans+=x; 28 for(int i=1;i<=n;++i)for(int j=1,x;j<m;++j)scanf("%d",&x),con(o[i][j],++pc,M),con(o[i][j+1],pc,M),con(pc,E,x),ans+=x; 29 for(int i=1;i<=n;++i)for(int j=1,x;j<m;++j)scanf("%d",&x),con(++pc,o[i][j],M),con(pc,o[i][j+1],M),con(0,pc,x),ans+=x; 30 while(bfs())ans-=dfs(0,M);printf("%d\n",ans); 31 }
employ人员雇佣
两人都雇+2w(i,j),雇一个-w(i,j),一个都不雇+0。建三叉戟。
可以认为:雇一个人需要额外付出w(i,j),而两个人同时雇会获得4w(i,j)。
怎么想到?解方程啊!

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define int long long 4 #define inf 12345678901234567ll 5 int fir[2000005],l[12000005],to[12000005],v[12000005],ecnt=1,cnt,ans; 6 int q[2000005],dep[2000005],n,t,cost[1005]; 7 void link(int a,int b,int vv){l[++ecnt]=fir[a];to[ecnt]=b;fir[a]=ecnt;v[ecnt]=vv;} 8 int bfs(){ 9 memset(dep,0,sizeof dep);dep[q[1]=t=1]=1; 10 for(int h=1;h<=t;++h)for(int i=fir[q[h]];i;i=l[i])if(v[i]&&!dep[to[i]]) 11 dep[q[++t]=to[i]]=dep[q[h]]+1; 12 return dep[2]; 13 } 14 int dfs(int p,int flow){ 15 int res=flow;if(p==2)return flow; 16 for(int i=fir[p];i;i=l[i])if(dep[to[i]]==dep[p]+1&&v[i]&&res){ 17 int q=dfs(to[i],min(v[i],res)); 18 if(!q)dep[to[i]]=0; 19 v[i]-=q;res-=q;v[i^1]+=q; 20 } 21 return flow-res; 22 } 23 signed main(){ 24 scanf("%lld",&n);cnt=2+n; 25 for(int i=1;i<=n;++i)scanf("%lld",&cost[i]); 26 for(int i=1,w;i<=n;++i)for(int j=1;j<=n;++j){ 27 scanf("%lld",&w);cost[i]+=w; 28 if(i<j)ans+=w<<2, 29 link(2+i,++cnt,inf),link(cnt,2+i,0), 30 link(2+j,cnt,inf),link(cnt,2+j,0), 31 link(cnt,2,w<<2),link(2,cnt,0); 32 } 33 for(int i=1;i<=n;++i)link(1,2+i,cost[i]),link(2+i,1,0);//printf("%lld\n",ans); 34 while(bfs())ans-=dfs(1,inf); 35 printf("%lld\n",ans); 36 }
关键在于对于每一对关系都新建了一个点,这样点的数量是$O(n^2)$的。
如果通过直接在两个点之间连边而不是三叉戟的话,就可以降为$O(n)$
解决方法是,雇佣每个人的代价还是$c_i+\sum\limits_{i=1}^{n} w(i,j)$
然后在两个人之间建边,即i向j连$2w(i,j)$。
当然还可以通过QJ数据A掉这道题,只要你不把w为0的边建出来就能没脸AC了。

1 #include<cstdio> 2 #define S 5000005 3 #define M 0x3ffffffffffff 4 #define int long long 5 int min(int a,int b){return a<b?a:b;} 6 int n,c[1001],w[1001][1001],fir[S],l[S],to[S],v[S],ec=1,pc,q[S],dep[S],ans,E; 7 void link(int a,int b,int V){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;v[ec]=V;} 8 void con(int a,int b,int V){link(a,b,V);link(b,a,0);} 9 bool bfs(){ 10 for(int i=1;i<=pc;++i)dep[i]=0; 11 for(int h=1,t=1;h<=t;++h)for(int i=fir[q[h]];i;i=l[i])if(!dep[to[i]]&&v[i]) 12 dep[q[++t]=to[i]]=dep[q[h]]+1; 13 return dep[E]; 14 } 15 int dfs(int p,int flow){ 16 if(p==E)return flow;int r=flow; 17 for(int i=fir[p];i;i=l[i])if(dep[to[i]]==dep[p]+1&&v[i]&&r){ 18 int x=dfs(to[i],min(r,v[i])); 19 if(!x)dep[to[i]]=0; 20 v[i]-=x;v[i^1]+=x;r-=x; 21 }return flow-r; 22 } 23 main(){ 24 scanf("%lld",&n);pc=E=n+1;dep[0]=1; 25 for(int i=1;i<=n;++i)scanf("%lld",&c[i]); 26 for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)scanf("%lld",&w[i][j]); 27 for(int i=1;i<=n;++i)for(int j=1+i;j<=n;++j)if(w[i][j]) 28 con(++pc,E,w[i][j]<<2),con(i,pc,M),con(j,pc,M),ans+=w[i][j]<<2,c[i]+=w[i][j],c[j]+=w[i][j]; 29 for(int i=1;i<=n;++i)con(0,i,c[i]); 30 while(bfs())ans-=dfs(0,M);printf("%lld\n",ans); 31 }
不同的最小割
最小割树的板子。
任选源汇求出最小割x,这个最小割会把集合划分为两个部分S与T。S内的点到T的点的最小割会对x取min。
再对两个集合分治下去,直到集合大小为1。过程中得到的所有最小割就是答案。
这样就只用做$O(n)$次网络流了。
至于怎么求出集合:就是从源点开始dfs,只走没有满流的边(即v还有值的边)所到达的点都属于S,没有dfs到的属于T。

1 #include<cstdio> 2 #include<iostream> 3 #include<set> 4 using namespace std; 5 set<int>ans; 6 int n,m,fir[888],l[18888],to[18888],v[18888],d[888],q[888],ec=1,S,E,cnt,a[888],al[888],t[888]; 7 void link(int a,int b,int V){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;v[ec]=V;} 8 bool bfs(){ 9 for(int i=1;i<=n;++i)d[i]=0;q[d[S]=1]=S; 10 for(int h=1,t=1;h<=t;++h)for(int i=fir[q[h]];i;i=l[i])if(v[i]&&!d[to[i]]) 11 d[q[++t]=to[i]]=d[q[h]]+1; 12 return d[E]; 13 } 14 int dfs(int p,int flow){int r=flow; 15 if(p==E)return flow; 16 for(int i=fir[p];i&&r;i=l[i])if(d[to[i]]==d[p]+1&&v[i]){ 17 int x=dfs(to[i],min(v[i],r)); 18 if(!x)d[to[i]]=0; 19 v[i]-=x;v[i^1]+=x;r-=x; 20 }return flow-r; 21 } 22 void DFS(int p){ 23 al[p]=1; 24 for(int i=fir[p];i;i=l[i])if(v[i]&&!al[to[i]])DFS(to[i]); 25 } 26 int dinic(int x=0){while(bfs())x+=dfs(S,0x3fffffff);return x;} 27 void Divide(int l,int r){ 28 if(l>=r)return; 29 for(int i=2;i<=ec;i+=2)v[i]=v[i^1]=v[i]+v[i^1]>>1; 30 S=a[l];E=a[r];ans.insert(dinic());DFS(S);int L=l-1,R=r+1; 31 for(int i=l;i<=r;++i)if(al[a[i]])t[++L]=a[i];else t[--R]=a[i]; 32 for(int i=1;i<=n;++i)al[i]=0; 33 for(int i=l;i<=r;++i)a[i]=t[i]; 34 Divide(l,L);Divide(R,r); 35 } 36 int main(){ 37 scanf("%d%d",&n,&m); 38 for(int i=1,x,y,V;i<=m;++i)scanf("%d%d%d",&x,&y,&V),link(x,y,V),link(y,x,V); 39 for(int i=1;i<=n;++i)a[i]=i; 40 Divide(1,n);printf("%u\n",ans.size()); 41 }
晨跑
最小费用最大流板子。要注意对于从1到n的直接连边只能走1次。所以边权(流量)不能是inf。

1 #include<cstdio> 2 int n,m,fir[444],l[44444],to[44444],pre[444],v[44444],w[44444],q[44444],d[444],iq[444],ec=1; 3 int day,ans; 4 void link(int a,int b,int V,int W){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;v[ec]=V;w[ec]=W;} 5 bool SPFA(){ 6 for(int i=1;i<=(n<<1|1);++i)d[i]=0x3fffffff;d[q[1]=3]=0; 7 for(int h=1,t=1;h<=t;iq[q[h]]=0,++h)for(int i=fir[q[h]];i;i=l[i])if(d[to[i]]>d[q[h]]+w[i]&&v[i]){ 8 pre[to[i]]=i;d[to[i]]=d[q[h]]+w[i]; 9 if(!iq[to[i]])iq[q[++t]=to[i]]=1; 10 }return d[n<<1]<0x3fffffff; 11 } 12 int main(){ 13 scanf("%d%d",&n,&m); 14 for(int i=1,x,y,W;i<=m;++i)scanf("%d%d%d",&x,&y,&W),link(x<<1|1,y<<1,1,W),link(y<<1,x<<1|1,0,-W); 15 for(int i=1;i<=n;++i)link(i<<1,i<<1|1,1,0),link(i<<1|1,i<<1,0,0); 16 while(SPFA()){day++;for(int i=pre[n<<1];i;i=pre[to[i^1]])ans+=w[i],v[i]--,v[i^1]++;} 17 printf("%d %d\n",day,ans); 18 }
80人环游世界
上下届无源汇最小费用可行流板子。
啊fixed by LNC:我写的是有源汇的但是我忘记为什么了

1 #include<cstdio> 2 int Ss=0,s=1,t=2,St=3,cn=3,n,m,dt[101][101],req[101],P[101][2]; 3 int fir[333],l[666666],to[666666],v[666666],c[666666],cnt=1,ans; 4 int pre[333],dep[333],q[66666],iq[333]; 5 void link(int a,int b,int w,int C){l[++cnt]=fir[a];fir[a]=cnt;to[cnt]=b;v[cnt]=w;c[cnt]=C;} 6 bool SPFA(){ 7 for(int i=1;i<=cn;++i)dep[i]=1234567890; 8 for(int h=1,t=1;h<=t;++h,iq[q[h]]=0)for(int i=fir[q[h]];i;i=l[i])if(v[i]&&dep[to[i]]>dep[q[h]]+c[i]){ 9 dep[to[i]]=dep[q[h]]+c[i];pre[to[i]]=i; 10 if(!iq[to[i]])q[++t]=to[i],iq[to[i]]=1; 11 } 12 return dep[St]!=1234567890; 13 } 14 int main(){ 15 scanf("%d%d",&n,&m); 16 for(int i=1;i<=n;++i)scanf("%d",&req[i]); 17 for(int i=1;i<n;++i)for(int j=i+1;j<=n;++j)scanf("%d",&dt[i][j]); 18 for(int i=1;i<=n;++i)P[i][0]=++cn,P[i][1]=++cn; 19 link(Ss,s,m,0);link(s,Ss,0,0); 20 link(t,St,m,0);link(St,t,0,0); 21 for(int i=1;i<=n;++i)link(s,P[i][0],1234567890,0),link(P[i][0],s,0,0); 22 for(int i=1;i<=n;++i)link(P[i][1],t,1234567890,0),link(t,P[i][1],0,0); 23 for(int i=1;i<=n;++i)link(Ss,P[i][1],req[i],0),link(P[i][1],Ss,0,0); 24 for(int i=1;i<=n;++i)link(P[i][0],St,req[i],0),link(St,P[i][0],0,0); 25 for(int i=1;i<=n;++i)for(int j=i+1;j<=n;++j)if(dt[i][j]!=-1) 26 link(P[i][1],P[j][0],1234567890,dt[i][j]),link(P[j][0],P[i][1],0,-dt[i][j]); 27 while(SPFA())for(int i=pre[St];i;i=pre[to[i^1]])v[i]--,v[i^1]++,ans+=c[i]; 28 printf("%d\n",ans); 29 }
修车
正难则反。还是拆点。把一个修车师傅拆成n个点,其中点d(i,j)表示第i个修车师傅修的倒数第j辆车。对于一辆时间为t的车,连向这个点的边权为t*j。
因为在它后面的所有车都需要等待t时间。因为它是倒数第j个,所以它后面有(j-1)个,算上他自己有j个,每个人都等t,所以是t×j。

1 #include<cstdio> 2 int n,m,t[666][100],num[100][666],cn,fir[6666],l[222222],to[222222],v[222222],c[222222],ans,cnt=1; 3 int iq[6666],q[222222],dt[6666],pre[6666]; 4 void con(int a,int b,int w,int C){l[++cnt]=fir[a];fir[a]=cnt;to[cnt]=b;v[cnt]=w;c[cnt]=C;} 5 void link(int a,int b,int C){con(a,b,1,C);con(b,a,0,-C);} 6 bool SPFA(){ 7 for(int i=1;i<=cn;++i)dt[i]=1234567890; 8 for(int h=1,t=1;h<=t;++h,iq[q[h]]=0)for(int i=fir[q[h]];i;i=l[i])if(v[i]&&dt[q[h]]+c[i]<dt[to[i]]){ 9 dt[to[i]]=dt[q[h]]+c[i];pre[to[i]]=i; 10 if(!iq[to[i]])iq[to[i]]=1,q[++t]=to[i]; 11 } 12 return dt[cn]!=1234567890; 13 } 14 int main(){ 15 scanf("%d%d",&m,&n);cn=n; 16 for(int i=1;i<=n;++i)link(0,i,0); 17 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)num[j][i]=++cn,scanf("%d",&t[i][j]); 18 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)for(int k=1;k<=n;++k)link(i,num[j][k],t[i][j]*k); 19 cn++; 20 for(int j=1;j<=m;++j)for(int k=1;k<=n;++k)link(num[j][k],cn,0); 21 while(SPFA())for(int i=pre[cn];i;i=pre[to[i^1]])ans+=c[i],v[i]--,v[i^1]++; 22 printf("%.2lf\n",ans*1.0/n); 23 }
数字配对
带权匹配问题。。。二分图才可做啊。
可以根据每个数分解质因数后质因子个数是奇偶数来分部。当然同部点不会连边,因为质数个数差为偶数的话就算能整除,商也是至少有2个质因子,是合数不连边。
但是我没有发现,我yy了一种联动边权。网络流在流经边A时也会使B的流量等量减少。
这样的话把每个点放在对偶图两边,一边消耗是另一边也消耗。
在不是二分图时会被hack。

1 #include<cstdio> 2 #include<iostream> 3 using namespace std; 4 #define M 10000005 5 #define E 2*n+1 6 int a[202],b[202],n,fir[405],l[M],to[M],v[M],ec=3,ans,iq[405],q[M],pre[M]; 7 long long w[M],dt[405],c[202],C; 8 void link(int a,int b,long long W,int V){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;w[ec]=W;v[ec]=V;} 9 bool isprime(int x){ 10 if(x==1)return 0; 11 for(int i=2;i*i<=x;++i)if(x%i==0)return 0; 12 return 1; 13 } 14 bool SPFA(){ 15 for(int i=1;i<=E;++i)dt[i]=0x3ffffffffffff; 16 for(int h=1,t=1;h<=t;iq[q[h]]=0,++h)for(int i=fir[q[h]];i;i=l[i]) 17 if(v[i]&&dt[to[i]]>dt[q[h]]+w[i]){ 18 dt[to[i]]=dt[q[h]]+w[i],pre[to[i]]=i; 19 if(!iq[to[i]])iq[q[++t]=to[i]]=1; 20 } 21 return dt[E]<0x3ffffffffffff; 22 } 23 main(){scanf("%d",&n); 24 for(int i=1;i<=n;++i)scanf("%d",&a[i]); 25 for(int i=1;i<=n;++i)scanf("%d",&b[i]); 26 for(int i=1;i<=n;++i)scanf("%lld",&c[i]); 27 for(int i=1;i<=n;++i)link(0,i,0,b[i]),link(i,0,0,0),link(i+n,E,0,b[i]),link(E,i+n,0,0); 28 for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)if(a[i]%a[j]==0&&isprime(a[i]/a[j])) 29 link(i,j+n,-c[i]*c[j],M),link(j+n,i,c[i]*c[j],0),link(j,i+n,-c[i]*c[j],M),link(i+n,j,c[i]*c[j],0); 30 while(SPFA()){ 31 int x=M;long long c=0; 32 for(int i=pre[E];i;i=pre[to[i^1]])x=min(x,v[i]),c+=w[i]; 33 if(C>=x*c){ans+=x,C-=x*c;for(int i=pre[E];i;i=pre[to[i^1]])v[i]-=x,v[i^1]+=x,v[i^2]-=x,v[i^3]+=x;} 34 else{ans+=C/c;break;} 35 }printf("%d\n",ans); 36 }
美食节
和《修车》一样。但是会T。
在跑增广路的时候,动态开点。不要都开出来,就可以了。

1 #include<cstdio> 2 int n,m,x[450],num[1005][8005],t[450][8005],cn,ans,tot; 3 int fir[222222],l[20000005],to[20000005],c[20000005],v[20000005],tt[20000005],cnt=1; 4 int iq[222222],q[222222],dt[222222],pre[222222],al[1005][8005]; 5 void link(int a,int b,int w,int C,int T){l[++cnt]=fir[a];fir[a]=cnt;to[cnt]=b;v[cnt]=w;c[cnt]=C;tt[cnt]=T;} 6 bool SPFA(){ 7 for(int i=1;i<=cn;++i)dt[i]=1234567890; 8 for(int h=1,t=1;h<=t;++h,iq[q[h]]=0)for(int i=fir[q[h]];i;i=l[i])if(dt[to[i]]>dt[q[h]]+c[i]&&v[i]){ 9 dt[to[i]]=dt[q[h]]+c[i];pre[to[i]]=i; 10 if(!iq[to[i]])q[++t]=to[i],iq[to[i]]=1; 11 } 12 return dt[cn]!=1234567890; 13 } 14 int main(){ 15 scanf("%d%d",&n,&m);cn=n; 16 for(int i=1;i<=n;++i)scanf("%d",&x[i]),link(0,i,x[i],0,0),link(i,0,0,0,0),tot+=x[i]; 17 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)scanf("%d",&t[i][j]); 18 for(int j=1;j<=m;++j)for(int k=1;k<=tot;++k)num[j][k]=++cn; 19 cn++; 20 for(int j=1;j<=m;++j)for(int k=1;k<=tot;++k)link(num[j][k],cn,1,0,0),link(cn,num[j][k],0,0,0); 21 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)for(int k=1;k<=1;++k) 22 link(i,num[j][k],1,t[i][j]*k,1),link(num[j][k],i,0,-t[i][j]*k,1); 23 while(SPFA()){ 24 for(int i=pre[cn];i;i=pre[to[i^1]]){ 25 v[i]--,v[i^1]++,ans+=c[i]; 26 int x=to[i],y=to[i^1],a; 27 if(!tt[i])continue; 28 if(x<y)continue;else x^=y^=x^=y; 29 for(int j=1;j<=m;++j)if(num[j][tt[i]]==y)a=j; 30 if(!al[a][tt[i]+1])for(int j=1;j<=n;++j)link(j,num[a][tt[i]+1],1,t[j][a]*(tt[i]+1),tt[i]+1),link(num[a][tt[i]+1],j,0,-t[j][a]*(tt[i]+1),tt[i]+1); 31 al[a][tt[i]+1]=1; 32 } 33 } 34 printf("%d\n",ans); 35 }



