[考试反思]1106csp-s模拟测试103: 渺茫
7点之前上不了博客,用gedit写的。谅解一下。
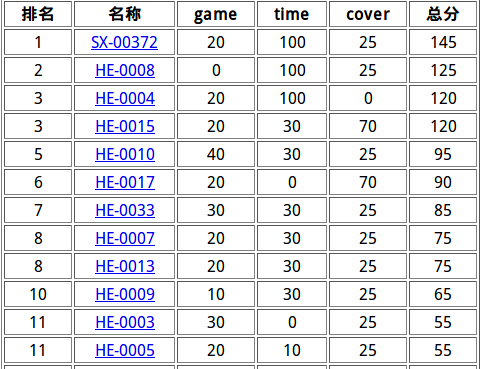

看起来不是特别惨?但是被sdfz爆踩了。。。
而且其实并不能说“不是特别惨”吧
90分算个啥啊?还凑不出个T2的AC
难易度评估错误,T2是最简单的没看出来。然后爆搜不够优秀TLE 0.
T1伪证的60分只有20,如果外层加一个clock就有40.。。
T3部分分打满,很明显了却没有想到启发式合并
说实在的还是经验不足实力不够,面对难题原型毕露(虽说相对于简单题稍微好一些)
T1:Game
先不考虑字典序,如何得到最高的积分?
贪心。这个好说。
但是在后面的操作中还需要修改牌序,导致局面变化,还要统计动态的积分。
就是说,你需要依次考虑每一位应该填什么,然后删除这张牌再check一下看积分变不变。
在积分不变的基础上,这一位越大越好。这满足单调性可以二分(稍后具体讲)
其实这类似于单点修改操作(挺抽象的)。
暴力贪心的话那么就需要从头再重新做一遍。
考虑如何优化?那只能是数据结构了。
线段树分治。(基于值域)
对于A和B有的牌都开一个权值线段树。考虑合并两个子树(即线段树update)操作。
右儿子的A和左儿子的B可以结合(满足大小关系),这些是可以获胜的局面,全局累加答案。
即设$win=min(A_{rc},B_{lc})$。那么在上传的时候,就有$ans+=win,A_p=A_{lc}+A_{rc}-win,B_p=B_{lc}+B_{rc}-win$
就是已经胜利的局面累加积分并且不再参与以后的运算。最后全局ans的值就是最大积分。
这就是最优决策。已经是用尽量小的A去战胜B了,等价于贪心。
单点修改的话直接重置某一个下标的AB值,整条链都修改一下就好。
在修改的时候要注意全局的ans应该要删除原来这个节点的贡献再修改并update,否则积分就会重复计算。
现在说明一下它的单调性(证明二分):其实并不是直接二分,也不是完全的单调性。
先考虑如果你赢了这一位,那么你用的值越大,得分可能越低(浪费了)
如果你输了这一位,那么你用的值大了,总得分可能也会降低(也是浪费)
如果你可以在赢下这一位的基础上保证总积分不变,那么你就会赢下这一位(因为这样的话字典序会更大)
所以二分的过程其实是:检查这一位能不能赢,如果可以就在$[b_i+1,max]$二分,如果不能赢就在$[1,b_i]$二分
找到最大取值,在线段树里删除,同时也要把B删除。逐位考虑即可。
可以拿multiset维护一下剩余A的最大值作为二分上届。不然有可能被卡常(只有我被卡了。。。)
复杂度$O(nlog^2n)$
%%%Rock_B教我看懂标程
%%%yxs暴力踩暴正解(比正解还难写还需要一大堆特殊性质,咱也不会打%%%就是了)
据说建树容易被卡常,传参好像比建树全局调用快一些。

1 #include<cstdio> 2 #include<set> 3 using namespace std; 4 multiset<int>S; 5 int n,a[100005],b[100005],cl[400005],cr[400005],A[400005],B[400005]; 6 int cnta[100005],cntb[100005],ans,rans; 7 void up(int p){ 8 int nw=min(B[p<<1],A[p<<1|1]); 9 ans+=nw;A[p]=A[p<<1]+A[p<<1|1]-nw;B[p]=B[p<<1]+B[p<<1|1]-nw; 10 } 11 void build(int p,int l,int r){ 12 cl[p]=l;cr[p]=r; 13 if(l==r){A[p]=cnta[l];B[p]=cntb[l];return;} 14 build(p<<1,l,l+r>>1);build(p<<1|1,(l+r>>1)+1,r); 15 up(p); 16 } 17 void modify(int p,int pos){ 18 if(cl[p]==cr[p]){A[p]=cnta[pos];B[p]=cntb[pos];return;} 19 ans-=min(B[p<<1],A[p<<1|1]); 20 if(pos<=cr[p<<1])modify(p<<1,pos); 21 else modify(p<<1|1,pos); 22 up(p); 23 } 24 bool chk(int x,int p,int de){ 25 cnta[x]--;modify(1,x); 26 int rA=ans+de; 27 cnta[x]++;modify(1,x); 28 return rA==rans; 29 } 30 int main(){ 31 freopen("game.in","r",stdin);freopen("game.out","w",stdout); 32 scanf("%d",&n); 33 for(int i=1;i<=n;++i)scanf("%d",&b[i]),cntb[b[i]]++; 34 for(int i=1;i<=n;++i)scanf("%d",&a[i]),cnta[a[i]]++,S.insert(a[i]); 35 build(1,1,*(--S.end()));rans=ans; 36 for(int i=1;i<=n;++i){ 37 cntb[b[i]]--;modify(1,b[i]); 38 int l=b[i]+1,r=*(--S.end()),ta=0; 39 while(l<=r)if(chk(l+r>>1,i,1))ta=l+r>>1,l=(l+r>>1)+1;else r=(l+r>>1)-1; 40 if(!ta){ 41 int L=1,R=b[i]; 42 while(L<=R)if(chk(L+R>>1,i,0))ta=L+R>>1,L=(L+R>>1)+1;else R=(L+R>>1)-1; 43 }else rans--; 44 cnta[ta]--,modify(1,ta);printf("%d ",ta);S.erase(S.find(ta)); 45 }puts(""); 46 }
T2:Time
贪心。不能直接做就要去发现特殊元素或特殊性质。
考场上一直以为最大值是特殊元素然后就卡死了。(因为会对其他元素产生影响)
实际上是要考虑最小值。它最后一定在两侧,考虑它是往左还是右移就好了。
如果一个数出现了多次,那么就依次考虑是最左边的数往左移还是最右边的数往右移就好了。

1 #include<cstdio> 2 #include<vector> 3 using namespace std; 4 vector<int>v[100005]; 5 int n,x[100005],t[100005];long long ans; 6 void add(int p,int w){for(;p<=n;p+=p&-p)t[p]+=w;} 7 int ask(int p,int a=0){for(;p;p^=p&-p)a+=t[p];return a;} 8 main(){ 9 freopen("time.in","r",stdin);freopen("time.out","w",stdout); 10 scanf("%d",&n); 11 for(int i=1;i<=n;++i)scanf("%d",&x[i]),v[x[i]].push_back(i),add(i,1); 12 for(int i=1;i<=100000;++i){ 13 int h=0,t=v[i].size()-1; 14 while(h<=t){ 15 int l=ask(v[i][h]-1),r=ask(n)-ask(v[i][t]); 16 if(l<r)ans+=l,add(v[i][h],-1),h++; 17 else ans+=r,add(v[i][t],-1),t--; 18 } 19 }printf("%lld\n",ans); 20 }
T3:Cover
首先看到“包含或不相交”就知道要建树,有父子关系。建一个超级父节点控制[1,n]避免它是森林。
因为我脑子很清奇所以我的建树比较诡异,所有区间(包括超级根节点)按照l为第一关键字从小到大,r为第二关键字从大到小排序。
这样排序之后,你就得到了这棵树的dfs序,然后根据“dfs序下一个点的子树是一段连续的区间”,用全局的单调指针递归建树即可(详见代码,这个讲不好)
然后尝试dp。
因为我脑子比较清奇所以我并没有像题解一样设出那个dp然后再差分。
我的dp定义是f[i][j]表示对于i这个点,你给它「第」j次覆盖的机会时所得到的「额外」收益。
所以我的dp一设出来就是题解里那个数组的差分。
考虑转移,我给这个点一次覆盖机会,那么它的决策要么是把机会下传给所有儿子,要么是就用来覆盖自己这个区间
那么$f[i][j]=\sum f[son][j]$。在这样得到f数组之后它是单调的(你会采取最优决策来让它收益最大化,最优决策一定会在第一次被取出,以此类推)
所以f[p][1]>=f[p][2]>=f[p][3]...然而这样并没有考虑这个点本身。
所以在这个本身已经有序的数组里插入$w_p$就好了。然后超级根节点的f数组前缀和一下就是答案。
那25的部分分就不需要维护有序数组,而是直接开桶,把“倒深度”放进去再做前缀和就好了。
因为除了叶节点以外,一个点的子树大小一定大于自身大小,所以有覆盖机会就下传就好了。
给出暴力代码。

1 #include<cstdio> 2 #include<algorithm> 3 #include<vector> 4 using namespace std; 5 vector<long long>v[300005]; 6 struct P{ 7 int l,r,w,o; 8 friend bool operator<(P a,P b){ 9 return a.l<b.l||(a.l==b.l&&a.r>b.r)||(a.l==b.l&&a.r==b.r&&a.o>b.o); 10 } 11 }ps[300005]; 12 long long ans,Ans[300005];int n,m,sz[300005],l[300005],to[300005],cnt,fir[300005],ald=2,spj=1; 13 void link(int a,int b){l[++cnt]=fir[a];fir[a]=cnt;to[cnt]=b;} 14 void dfs(int p){ 15 for(int i=fir[p];i;i=l[i])dfs(to[i]),sz[p]=max(sz[p],sz[to[i]]); 16 sz[p]++;v[p].resize(sz[p]); 17 for(int i=fir[p];i;i=l[i])for(int j=0;j<sz[to[i]];++j)v[p][j]+=v[to[i]][j]; 18 v[p][sz[p]-1]=ps[p].w; 19 sort(v[p].begin(),v[p].end());reverse(v[p].begin(),v[p].end()); 20 } 21 void build(int p){while(ps[p].l<=ps[ald].l&&ps[ald].r<=ps[p].r)link(p,ald),ald++,build(ald-1);} 22 int DFS(int p){ 23 int dep=1; 24 for(int i=fir[p];i;i=l[i])dep=max(dep,DFS(to[i])+1); 25 Ans[dep]+=ps[p].w; 26 return dep; 27 } 28 int main(){freopen("cover.in","r",stdin);freopen("cover.out","w",stdout); 29 scanf("%d%d",&n,&m); 30 for(int i=1;i<=m;++i)scanf("%d%d%d",&ps[i].l,&ps[i].r,&ps[i].w),ps[i].o=i,ps[i].r--; 31 m++;ps[m]=(P){1,n,0,m}; 32 for(int i=2;i<m;++i)if(ps[i].w!=ps[1].w)spj=0; 33 sort(ps+1,ps+1+m);build(1); 34 if(spj){DFS(1);for(int i=1;i<m;++i)Ans[i]+=Ans[i-1],printf("%lld ",Ans[i]);return 0;} 35 dfs(1); 36 v[1].resize(m); 37 for(int i=1;i<m;++i)ans+=v[1][i-1],printf("%lld ",ans);puts(""); 38 }
如果用数组维护,时空都无法接受,考虑用数据结构。
需要支持的操作:插入一个值,不断取出最大值。(然后删除,这样次大值就变成了最大值,就可以依次取出并加和了)
大根堆。优先队列。
然而就这样空间对了时间复杂度还是有问题。
启发式合并,把重儿子的队列直接接过来,然后再与其它儿子合并。
复杂度$O(nlog^2n)$,并不知道是不是正解复杂度(为什么出了300000?)
update:我又害人了我写挂了,复杂度写成$O(n^2logn)$了。

1 #include<cstdio> 2 #include<algorithm> 3 #include<queue> 4 using namespace std; 5 priority_queue<long long>v[300005],r; 6 struct P{ 7 int l,r,w; 8 friend bool operator<(P a,P b){ 9 return a.l<b.l||(a.l==b.l&&a.r>b.r); 10 } 11 }ps[300005]; 12 long long ans,Ans[300005];int n,m,sz[300005],l[300005],to[300005],cnt,fir[300005],ald=2,spj=1; 13 void link(int a,int b){l[++cnt]=fir[a];fir[a]=cnt;to[cnt]=b;} 14 void dfs(int p){ 15 for(int i=fir[p];i;i=l[i])dfs(to[i]),sz[p]=max(sz[p],sz[to[i]]); 16 sz[p]++; 17 for(int i=fir[p];i;i=l[i])if(sz[to[i]]+1==sz[p]){swap(v[p],v[to[i]]);to[i]=0;break;} 18 for(int i=fir[p];i;i=l[i])if(to[i]){ 19 while(!v[to[i]].empty())r.push(v[p].top()+v[to[i]].top()),v[p].pop(),v[to[i]].pop(); 20 swap(r,v[p]);while(!r.empty())v[p].push(r.top()),r.pop(); 21 }v[p].push(ps[p].w); 22 } 23 void build(int p){while(ps[p].l<=ps[ald].l&&ps[ald].r<=ps[p].r)link(p,ald),ald++,build(ald-1);} 24 int main(){freopen("cover.in","r",stdin);freopen("cover.out","w",stdout); 25 scanf("%d%d",&n,&m); 26 for(int i=1;i<=m;++i)scanf("%d%d%d",&ps[i].l,&ps[i].r,&ps[i].w),ps[i].r--; 27 m++;ps[m]=(P){1,n,0}; 28 sort(ps+1,ps+1+m);build(1); 29 dfs(1); 30 for(int i=1;i<=m;++i)v[1].push(0); 31 for(int i=1;i<m;++i)ans+=v[1].top(),v[1].pop(),printf("%lld ",ans); 32 }

1 #include<cstdio> 2 #include<algorithm> 3 #include<queue> 4 using namespace std; 5 priority_queue<long long>v[300005],r; 6 struct P{ 7 int l,r,w; 8 friend bool operator<(P a,P b){ 9 return a.l<b.l||(a.l==b.l&&a.r>b.r); 10 } 11 }ps[300005]; 12 long long ans,Ans[300005];int n,m,sz[300005],l[300005],to[300005],cnt,fir[300005],ald=2,spj=1; 13 void link(int a,int b){l[++cnt]=fir[a];fir[a]=cnt;to[cnt]=b;} 14 void dfs(int p){ 15 for(int i=fir[p];i;i=l[i])dfs(to[i]),sz[p]=max(sz[p],sz[to[i]]); 16 sz[p]++; 17 for(int i=fir[p];i;i=l[i])if(sz[to[i]]+1==sz[p]){swap(v[p],v[to[i]]);to[i]=0;break;} 18 for(int i=fir[p];i;i=l[i])if(to[i]){ 19 while(!v[to[i]].empty())r.push(v[p].top()+v[to[i]].top()),v[p].pop(),v[to[i]].pop(); 20 while(!r.empty())v[p].push(r.top()),r.pop(); 21 }v[p].push(ps[p].w); 22 } 23 void build(int p){while(ps[p].l<=ps[ald].l&&ps[ald].r<=ps[p].r)link(p,ald),ald++,build(ald-1);} 24 int main(){freopen("cover.in","r",stdin);freopen("cover.out","w",stdout); 25 scanf("%d%d",&n,&m); 26 for(int i=1;i<=m;++i)scanf("%d%d%d",&ps[i].l,&ps[i].r,&ps[i].w),ps[i].r--; 27 m++;ps[m]=(P){1,n,0}; 28 sort(ps+1,ps+1+m);build(1); 29 dfs(1); 30 for(int i=1;i<=m;++i)v[1].push(0); 31 for(int i=1;i<m;++i)ans+=v[1].top(),v[1].pop(),printf("%lld ",ans); 32 }



