[考试反思]1031csp-s模拟测试96:常态
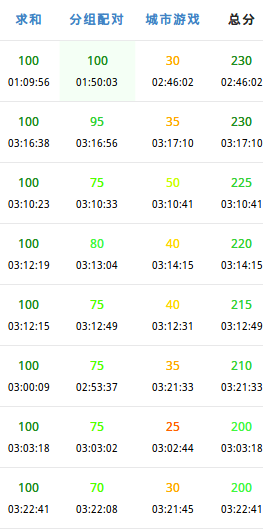

按照smily的说法这一场的大众分暴力分是不是265啊QwQ那我可真是个大垃圾
总算还是回归了常态。
T3文件名写错,把“city.in”写成“city,in”
还好,只丢了20分。
T2乱打$O(n^2 \ log^2n)$数据水拿了$95pts$
T1慢速乘yy一下就没了。
然后其实很垃圾。特别困,状态很差,脑子也动不起来了。
于是一直在打。打完暴力打对拍,偶尔停下来想一想。
T2想到了正解但是不会证复杂度所以没有打(这个倍增思路被我在考场上YY出来很多次但是一直觉得它的复杂度不对所以没打过。。。)
但是当我在9:35挂上T2的对拍发现我RE不输出的时候我就是到事情不太妙。(考后看到交上去的代码WA 0了)
这次考试不是210分钟而是205分钟所以更加紧迫。赶忙gdb发现是剪枝挂了,干掉剪枝就没事了。
对拍很重要啊!
T1:求和
算是个慢速乘板子。快速乘据说会炸精。

1 #include<cstdio> 2 #define LL long long 3 LL mod,a,b,c,d; 4 LL mult(LL b,LL t,LL a=0){ 5 b%=mod; 6 for(;t;t>>=1,b+=b){ 7 if(b>=mod)b-=mod; 8 if(t&1)a+=b; 9 if(a>=mod)a-=mod; 10 } 11 return a; 12 } 13 int main(){ 14 freopen("sum.in","r",stdin); 15 freopen("sum.out","w",stdout); 16 scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&mod); 17 LL X=c-a+1,Y=d-b+1,x=a+c,y=b+d,ans=0; 18 if(X&1)ans+=mult(mult(X,x>>1),Y); 19 else ans+=mult(mult(X>>1,x),Y); 20 if(Y&1)ans+=mult(mult(Y,y>>1),X); 21 else ans+=mult(mult(Y>>1,y),X); 22 ans-=mult(X,Y); 23 if(ans<0)ans+=mod; 24 if(ans>mod)ans-=mod; 25 printf("%lld\n",ans); 26 }
T2:分组配对
最有配对方案一定是最大的与最大的配,第二与第二配。
应该不需要证明吧,简单的数学推导。
然后这是$O(n^2 \ log^2n)$的暴力

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 int n,a[500005],b[500005],ra[500005],rb[500005],ans,high[500005]; 5 long long M,sum[500005]; 6 bool chk(int l,int r){ 7 if(sum[r]-sum[l-1]>M)return false; 8 for(int i=l;i<=r;++i)ra[i]=a[i],rb[i]=b[i]; 9 sort(ra+l,ra+r+1);sort(rb+l,rb+r+1); 10 long long A=0; 11 for(int i=l;i<=r;++i)A+=1ll*ra[i]*rb[i]; 12 return A<=M; 13 } 14 int main(){ 15 freopen("pair.in","r",stdin); 16 freopen("pair.out","w",stdout); 17 scanf("%d%lld",&n,&M); 18 for(int i=1;i<=n;++i)scanf("%d",&a[i]); 19 for(int i=1;i<=n;++i)scanf("%d",&b[i]); 20 for(int i=1;i<=n;++i)sum[i]=sum[i-1]+1ll*a[i]*b[i]; 21 for(int i=0;i<20;++i)for(int j=1<<i;j<1<<i+1&&j<=n;++j)high[j]=i; 22 for(int i=1;i<=n;){ 23 int l=i,r=n;ans++; 24 while(l<r-1)if(chk(i,l+r>>1))l=l+r>>1;else r=(l+r>>1)-1; 25 if(chk(i,r))i=r+1;else i=l+1; 26 }printf("%d\n",ans); 27 }
实际上套一个先倍增后二分就能解决二分界过大的问题。
进阶指南的原题,不细说(之前没好好看书。。。)

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 int n,a[500005],b[500005],ra[500005],rb[500005],ans,high[500005]; 5 long long M,sum[500005]; 6 bool chk(int l,int r){ 7 if(sum[r]-sum[l-1]>M)return false; 8 for(int i=l;i<=r;++i)ra[i]=a[i],rb[i]=b[i]; 9 sort(ra+l,ra+r+1);sort(rb+l,rb+r+1); 10 long long A=0; 11 for(int i=l;i<=r;++i)A+=1ll*ra[i]*rb[i]; 12 return A<=M; 13 } 14 int main(){ 15 freopen("pair.in","r",stdin); 16 freopen("pair.out","w",stdout); 17 scanf("%d%lld",&n,&M); 18 for(int i=1;i<=n;++i)scanf("%d",&a[i]); 19 for(int i=1;i<=n;++i)scanf("%d",&b[i]); 20 for(int i=1;i<=n;++i)sum[i]=sum[i-1]+1ll*a[i]*b[i]; 21 for(int i=1;i<=n;){ 22 int l,r,j;ans++; 23 for(j=0;i+(1<<j)-1<=n;++j)if(!chk(i,i+(1<<j)-1)){l=i+(1<<j-1)-1;r=i+(1<<j)-2;break;} 24 if(i+(1<<j)-1>n)l=i+(1<<j-1)-1,r=n; 25 while(l<r-1)if(chk(i,l+r>>1))l=l+r>>1;else r=(l+r>>1)-1; 26 if(chk(i,r))i=r+1;else i=l+1; 27 }printf("%d\n",ans); 28 }
T3:城市游戏
神仙。难想。
抄题解就好了。
设$f_i$表示现在小B还没有封路过,这时候小A在最优决策下走到n号点的距离。
考虑转移,设$d_{i,j}$表示$i - j$这条路径被封上之后,从i到n的最短路。
那么转移的方程就是$f_i=min(max(f_j+dis_{i,j},d_{i,j}))$。$dis$是边的长度。
注意这个$min$和$max$的嵌套,它的具体含义就是小B会在里面的两种决策里选择最优的,而小A在考虑所有小B的可能的决策后选择最优的。
内层的具体含义就是如果现在立刻封路,那么现在小A的剩余距离就是$d_{i,j}$。剩下的一种决策就是不拦着小A让他随便继续走,以后再封路。
$f_n=0$。倒着推回去就好了。具体做法就是$Dijkstra$。把$max$里面的东西当做边权跑最短路。
因为是倒推,所以对$f$定义的理解也要倒着想。
现在没有封路的话,那么就可以选择两种:
一种是立刻封掉下一条路,然后不再封路,一种是先不动让小A继续走,然后以后再封,取以后的最优决策$f_j$。
构造以n为根的最短路径树,这样就能得到每个点到他的祖先点的距离。同时也就能得到每个点到n的距离。
所以就是从n号点再跑一个$Dijkstra$得到最短路,记录前驱边,用前驱边建树。
如果小B不封最短路树上的边,那么小A就会直接按照最短路树上的边走到n。
所以必须封一条最短路径树上的边$(u,v)$。这么一封,树就断成了两个联通块。
如果$u$是父亲的话,那么两个联通块一个是以$v$为根的子树,另一个是原树的剩余部分。
想要替代这条被封的边的话,那么一定会走一条边$(a,b)$且$a,b$分别属于两个联通块。
比较明显啊,如果属于同一个联通块那么$u,v$还是不联通啊没有替代原边的效果。
替代之后,从$v$到$n$的最短距离就是$dt[a]+dt[b]+dis_{a,b}-dt[v]$。
其中$dt$表示每个节点到n号点的最短路。画个图就明白了不细说。
这样的话我们就能得到$d$数组了。但是复杂度还是不对的。
换一个思路,我们考虑每一条树外边的贡献。
它能让什么样的树边所断开的联通块重新联通呢?条件是$a \in subtree(v) \ and \ b \notin subtree(v)$
再进一步,当且仅当$v$在$a$或$b$的祖先链上(那么一个在$v$子树里一个在子树外)。
但又不能同时在$a,b$的祖先链上(那么就都在子树外了)。
那么就是$lca$以下的祖先链部分了。
边权下放到儿子,那么用儿子的权值代表父边的话,就是$a$到$lca$和$b$到$lca$,不含$lca$
最后得到的就是$w_i=d_{fa_i,i}$
链上更新取$min$。可以用题解里说的神仙的并查集,但树链剖分貌似更加显然(复杂度都多了一个$log$)
然而复杂度什么的并不是问题,其实爆跳父亲跳到$lca$不断更新即可。
俩$Dijkstra$一个$dfs$。代码还是挺好写的。

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define LL long long 4 #define S 100005 5 #define inf 100000000000000000 6 priority_queue<pair<LL,int>,vector<pair<LL,int> >,greater<pair<LL,int> > >q; 7 int fir[S],l[S<<2],to[S<<2],ec=1,n,m,Q[S],pre[S],FIR[S],L[S],TO[S],EC,f[18][S],dep[S]; 8 char al[S],iq[S],nt[S<<2],AL[S],it[S<<2];LL dt[S],ans,DT[S],w[S<<2],dp[S]; 9 void link(int a,int b,int v){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;w[ec]=v;} 10 void LINK(int a,int b){L[++EC]=FIR[a];FIR[a]=EC;TO[EC]=b;} 11 void dfs(int p){ 12 for(int i=1;i<18;++i)f[i][p]=f[i-1][f[i-1][p]];dep[p]=dep[f[0][p]]+1; 13 for(int i=FIR[p];i;i=L[i])f[0][TO[i]]=p,dfs(TO[i]); 14 } 15 int lca(int a,int b){ 16 int subdep=dep[a]-dep[b]; 17 if(subdep<0)subdep*=-1,a^=b^=a^=b; 18 for(int i=17;~i;--i)if(subdep&1<<i)a=f[i][a]; 19 if(a==b)return a; 20 for(int i=17;~i;--i)if(f[i][a]!=f[i][b])a=f[i][a],b=f[i][b]; 21 return f[0][a]; 22 } 23 int main(){ 24 freopen("city.in","r",stdin);freopen("city.out","w",stdout); 25 scanf("%d%d",&n,&m); 26 for(int i=1,x,y,v;i<=m;++i)scanf("%d%d%d",&x,&y,&v),link(x,y,v),link(y,x,v); 27 for(int i=1;i<n;++i)DT[i]=dt[i]=dp[i]=inf; 28 q.push(make_pair(0,n)); 29 while(!q.empty()){ 30 int p=q.top().second; q.pop(); 31 if(AL[p])continue;AL[p]=1; 32 for(int i=fir[p];i;i=l[i])if(DT[to[i]]>DT[p]+w[i]) 33 pre[to[i]]=i,q.push(make_pair(DT[to[i]]=DT[p]+w[i],to[i])); 34 } 35 for(int i=1;i<n;++i)LINK(to[pre[i]^1],i),it[pre[i]]=it[pre[i]^1]=1; 36 dfs(n); 37 for(int i=1;i<=m;++i)if(!it[i<<1]){ 38 int a=to[i<<1],b=to[i<<1|1],LCA=lca(a,b);LL val=DT[a]+DT[b]+w[i<<1]; 39 while(a!=LCA)dp[a]=min(dp[a],val-DT[a]),a=f[0][a]; 40 while(b!=LCA)dp[b]=min(dp[b],val-DT[b]),b=f[0][b]; 41 } 42 q.push(make_pair(0,n)); 43 while(!q.empty()){ 44 int p=q.top().second; q.pop(); 45 if(al[p])continue;al[p]=1; 46 for(int i=fir[p];i;i=l[i])if(dt[to[i]]>max(dt[p]+w[i],it[i]?dp[to[i]]:DT[to[i]])) 47 q.push(make_pair(dt[to[i]]=max(dt[p]+w[i],it[i]?dp[to[i]]:DT[to[i]]),to[i])); 48 }printf("%lld\n",dt[1]>=inf?-1:dt[1]); 49 }



