[考试反思]1030csp-s模拟测试94:未知
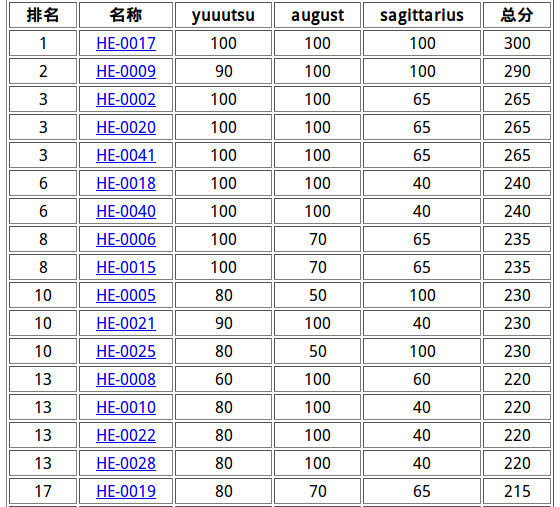
排名也未知。第1或第5。
分数也未知,300或260。
人生真是大起大落。。。

啊啊啊啊啊我好感动啊竟然重测了一次~~~~~
评测机怎么测怎么RE,本机怎么测怎么AC(任意编译指令,任意评测平台)
结果原来是系统栈空间开小了导致递归爆栈了啊。
重测就是把栈空间开到内存限制的大小然后我的代码就没锅了。
然后去隔壁用评测机调了一个小时也找不到RE的原因。。。
也许是对考场上全程无摸鱼一直在思考的奖励吧。。。
然而B哥又被防AK了也是稍惨。
人生第一次AK非B组题,还是有一点激动。。。
出题人部分分给的很好,难得有提示意义。
好事就是让我这个傻子也想出来了,坏事就是所有人的分数都很高%%%。
所以想在总分上凭这一场来翻身还是妄想。
继续加油,没有懈怠的机会。
毕竟又不是谁都像skyh一样两场不考都对排名没影响。。。
upd:人生真是大起大落我又260了没AK我感觉我在farting。。。为什么要这么调戏我的感情啊。。。
T1:凉宫春日的忧郁
写高精就好了,留300位精度绝对炸不了。
其实double就够了。求log精度更高。(好像并没有300位+比较位数的精度高)

1 //remember to submit 2 #include<cstdio> 3 int max(int a,int b){return a>b?a:b;} 4 struct Int{ 5 long long a[50005];int ws; 6 #define mod 1000000000000 7 friend void operator*=(Int &x,int p){ 8 int W=max(x.ws-25,0); 9 for(int i=x.ws;i>=W;--i)x.a[i]*=p; 10 for(int i=W;i<=x.ws;++i)x.a[i+1]+=x.a[i]/mod,x.a[i]%=mod; 11 if(x.a[x.ws+1])x.ws++; 12 } 13 friend bool operator<=(Int x,Int y){ 14 if(x.ws!=y.ws)return x.ws<y.ws; 15 for(int i=x.ws;~i;--i)if(x.a[i]!=y.a[i])return x.a[i]<y.a[i]; 16 return true; 17 } 18 void reset(){ 19 for(int i=ws;~i;--i)a[i]=0; 20 ws=0;a[0]=1; 21 } 22 }fc,pw; 23 int main(){ 24 freopen("yuuutsu.in","r",stdin); 25 freopen("yuuutsu.out","w",stdout); 26 int t,x,y;scanf("%d",&t); 27 while(t--){ 28 scanf("%d%d",&x,&y); 29 fc.reset();pw.reset(); 30 while(y--)fc*=y+1,pw*=x; 31 puts(pw<=fc?"Yes":"No"); 32 } 33 }
T2:漫无止境的八月
差分。之后操作就是在相距k的位置上一加一减。
其它位互不影响。所以把数组下标直接对k取模即可。
差分的特殊之处在于如果你对序列末尾操作的话会在位置n+1进行加减,而这个位置是几其实是没有关系的。
所以同余于n+1的位置是否为0不会对答案产生影响。特判。
修改的话差分数组只改变了两个位置,判断是否有新的0出现或消失即可。

1 //remember to submit 2 #include<cstdio> 3 int n,k,q,cnt,p;long long x[2000005]; 4 int read(){ 5 register int p=0,nt=0;register char ch=getchar(); 6 while(ch<'0'||ch>'9')nt=ch=='-',ch=getchar(); 7 while(ch<='9'&&ch>='0')p=(p<<3)+(p<<1)+ch-48,ch=getchar(); 8 return nt?-p:p; 9 } 10 int main(){ 11 freopen("august.in","r",stdin); 12 freopen("august.out","w",stdout); 13 n=read();k=read();q=read(); 14 for(int i=1;i<=n;++i)x[i]=read(); 15 for(int i=n;i;--i)x[i]=x[i]-x[i-1]; 16 for(int i=k;i<=n;++i)x[i%k]+=x[i]; 17 for(int i=0;i<k;++i)if(x[i])cnt++; 18 p=(n+1)%k; 19 if(x[p])cnt--; 20 puts(cnt?"No":"Yes"); 21 for(int i=1,a,b,p1,p2;i<=q;++i){ 22 a=read(),b=read(); 23 p1=a%k;p2=(a+1)%k; 24 if(p1!=p&&x[p1])cnt--; 25 if(p2!=p&&x[p2])cnt--; 26 x[p1]+=b;x[p2]-=b; 27 if(p1!=p&&x[p1])cnt++; 28 if(p2!=p&&x[p2])cnt++; 29 puts(cnt?"No":"Yes"); 30 } 31 }
T3:射手座之日
我复杂度是错的,极端情况下是$O(\frac{n^2}{k})$,其中k是一个基于数据的常数
具体范围我也不知道,我只知道$4 \leq k \leq n$
但是可以优化到稳定的$O(nlogn)$,常数会很大,和B哥一样。
看特殊性质部分分,a序列就是dfs序。
那么问题就是对于每一个子区间[l,r]找到最大的p满足$dfn[p]<=l$且$r<=dfr[p]$
其中$dfn/dfr$表示p子树的dfs序区间。
而“最大这个限制不好处理,我们把权值做一遍树上差分,这样的话问题就转化成了:对于每一个子区间[l,r]找到所有的p满足$dfn[p]<=l$且$r<=dfr[p]$
枚举p,它的控制区间内的所有子区间都满足条件,那么答案就是
$\sum\limits_{i=1}^{n} \frac{y[i] \times (dfr[i]-dfn[i]+1) \times (dfr[i]-dfn[i]+2)}{2}$
其中$y$就是$x$数组在树上差分之后的数组,即$y[i]=x[i]-x[f_i]$
而没有了特殊性质之后怎么做?
外层还是枚举p的话,内层的式子就不一样了,是满足上面条件的子区间数。
其实不考虑有包含关系的子区间,那么答案就是$y[i] \times \sum \frac{(r-l+1)\times(r-l+2)}{2}$
问题在于求出所有极长子区间。(极长是指不被包含的区间,如[l,r]存在时[l,r-1]不可能存在,而[1,4][7,9]可以共存)
把问题带到树上,考虑一个叶子节点,它的合法区间就是一个点。
其实对于每一个点它最开始的合法区间都是自己那一个点,后面还要合并上子树内的所有点。
考虑怎么合并。
因为a是一个排列,所以这些区间当然不会有交集,那么我们可以用一个类似与归并排序的过程来合并区间。
合并的过程中如果遇到$[L,p]+[p+1,R]$这样的两个区间,那么就把它合并成一个。
在回溯的同时统计$vector$里面的所有极长区间累加答案即可。
当然这个复杂度不对,虽然也不是很好卡(出题人想不到有这种打法)
然而正解的一种是不再用$vector$归并,而是直接用树上线段树启发式合并来维护极长区间。
时间复杂度是$O(nlogn)$的。
因为LNC说我数据结构必挂所以考场上还真的没有打数据结构2333

1 //remember to submit 2 #include<cstdio> 3 #include<vector> 4 #include<algorithm> 5 using namespace std; 6 vector<int>L[200005],R[200005],reL,reR; 7 int ec,fir[200005],l[200005],to[200005],x[200005],y[200005],dfn[200005],dfr[200005]; 8 int a[200005],tim,n,pos[200005];long long ans; 9 void link(int a,int b){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;} 10 void dfs(int p,int fa){ 11 y[p]=x[p]-x[fa]; dfn[p]=++tim; 12 for(int i=fir[p];i;i=l[i])if(to[i]!=fa)dfs(to[i],p); 13 dfr[p]=tim; 14 } 15 void pushin(int l,int r){ 16 if(reL.empty()||reR[reR.size()-1]!=l-1)return reL.push_back(l),reR.push_back(r),(void)0; 17 reR[reR.size()-1]=r; 18 } 19 void DFS(int p,int fa){ 20 L[p].push_back(pos[dfn[p]]);R[p].push_back(pos[dfn[p]]); 21 for(int i=fir[p];i;i=l[i])if(to[i]!=fa){ 22 DFS(to[i],p); 23 int p1=0,p2=0,e1=L[p].size(),e2=L[to[i]].size(); 24 while(p1<e1&&p2<e2)if(L[p][p1]<L[to[i]][p2])pushin(L[p][p1],R[p][p1]),p1++; 25 else pushin(L[to[i]][p2],R[to[i]][p2]),p2++; 26 while(p1<e1)pushin(L[p][p1],R[p][p1]),p1++; 27 while(p2<e2)pushin(L[to[i]][p2],R[to[i]][p2]),p2++; 28 swap(reL,L[p]);swap(reR,R[p]); 29 reL.clear();reR.clear();L[to[i]].clear();R[to[i]].clear(); 30 }int sz=L[p].size(); 31 for(int i=0;i<sz;++i)ans+=(R[p][i]-L[p][i]+1ll)*(R[p][i]-L[p][i]+2ll)/2*y[p]; 32 } 33 int main(){ 34 freopen("sagittarius.in","r",stdin); 35 freopen("sagittarius.out","w",stdout); 36 scanf("%d",&n); 37 for(int i=2,f;i<=n;++i)scanf("%d",&f),link(f,i); 38 for(int i=1;i<=n;++i)scanf("%d",&a[i]); 39 for(int i=1;i<=n;++i)scanf("%d",&x[i]); 40 dfs(1,0); 41 for(int i=1;i<=n;++i)a[i]=dfn[a[i]],pos[a[i]]=i; 42 DFS(1,0); 43 printf("%lld\n",ans); 44 }


