[考试反思]1028csp-s模拟测试91:预估
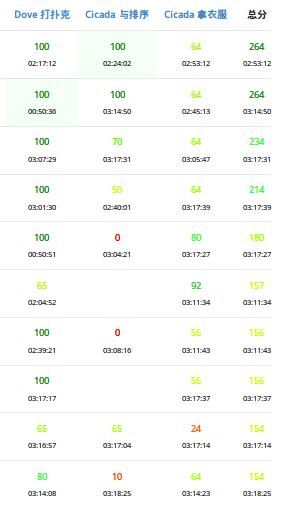

这一轮是要闹哪样啊???前十都死活进不去???
能不能不要到联赛前突然连续掉链子啊!!!
总算难得的切掉了T1。然后又一次把T2和T3的难度估反了
结果给T2剩下了30分钟,想到正解来不及打了。
然后T3没有乱搞丢了很多分。(循环不用跑满,上限能到80。。。考后还有AC的)
联赛题目的难度基本是升序。。。
学会乱搞,要有信仰。。。
T1必须占用更少的时间,想到并证明正确之后就快速打出来
T1:Dave打扑克
可以证明,数量本质不同的堆数至多为根号个。
所以并查集维护,用unordered_set迭代器遍历,用树状数组计数询问即可。

1 #include<cstdio> 2 #include<unordered_set> 3 using namespace std; 4 unordered_set<int>S; 5 int n,m,t[200005],buc[200005],siz[100005],f[100005]; 6 void add(int p,int w){for(;p<=200000;p+=p&-p)t[p]+=w;} 7 int ask(int p,int a=0){for(;p;p^=p&-p)a+=t[p];return a;} 8 int find(int p){return f[p]==p?p:f[p]=find(f[p]);} 9 int main(){//freopen("cards105.in","r",stdin);freopen("my.out","w",stdout); 10 scanf("%d%d",&n,&m); 11 buc[1]=n;S.insert(1);add(1,n); 12 for(int i=1;i<=n;++i)f[i]=i,siz[i]=1; 13 for(int i=1,opt,x,y;i<=m;++i){ 14 scanf("%d",&opt); 15 if(opt==1){ 16 scanf("%d%d",&x,&y); 17 x=find(x);y=find(y); 18 if(x==y)continue; 19 add(siz[x],-1);add(siz[y],-1);add(siz[x]+siz[y],1); 20 buc[siz[x]]--;buc[siz[y]]--;buc[siz[x]+siz[y]]++; 21 if(!buc[siz[x]])S.erase(siz[x]); 22 if(!buc[siz[y]])S.erase(siz[y]); 23 if(buc[siz[x]+siz[y]]==1)S.insert(siz[x]+siz[y]); 24 siz[y]+=siz[x];f[x]=y;n--; 25 }else{ 26 scanf("%d",&x);long long ans=n*(n-1ll)>>1; 27 if(!x){printf("%lld\n",ans);continue;} 28 unordered_set<int>::iterator it=S.begin(); 29 while(it!=S.end()){ 30 y=*it; 31 ans-=1ll*buc[y]*(ask(y+x-1)-ask(y)); 32 ans-=1ll*buc[y]*(buc[y]-1)>>1; 33 it++; 34 }printf("%lld\n",ans); 35 } 36 } 37 }
T2:Cicada与排序
归并排序每个数也就会递归下去log层。
所以我们不断考虑每个数在参与一次归并后的相对排名就好了。
当然数字不一样的最后排名肯定好说,现在只考虑每个数在所有与它相同的数里的相对排名(以下简称“位置”)
设rk[i][j]表示最开始位置在i的数在归并后所在的位置。
然后我们考虑如何转移,我们需要的其实就是一个“两个数组归并,其中第一个数组的第p位在归并后的数组排第q位的概率”
这个可以dp求出。dp[i][j][0/1]表示归并排序时第一个数组弹掉了i个,第二个数组弹掉了j个,最后一次弹的来自于第一组还是第二组。
这样的话最后弹掉的元素就是排名第i+j的元素了,而在归并之前的排名就是i或j(取决于来源)
具体的转移其实就是考虑两个数组是不是已经被弹干净了,弹干净了一个那就只能弹另一个,否则就随机弹一个
转移比较简单,自己想比较好(这个已经比题解的那个简单很多了)实在不行再颓码
这个dp数组当然与两个原数组的长度有关,所以要放在merge_sort里面处理,而非全局预处理(这不是题解思路)
然后rk也就可以转移了,枚举归并前后的排名即可。
不要memset。跑的很快的。
复杂度的证明可能要等到学积分?极端数据是所有数都相同。
并不是积分,是主定理啦!
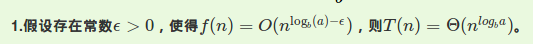
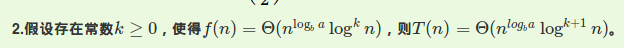
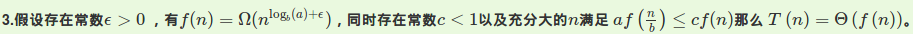
这道题满足第三条。$f(n)=\Omega (n^3)$,
这样的话$\epsilon =2>0$
此时c取$\frac{1}{4}$时满足后者条件即
$2f(\frac{n}{2})<=\frac{1}{4}f(n)$,其中$a=b=2$
所以总复杂度$O(n^3)$

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define mod 998244353 4 #define inv 499122177 5 #define int long long 6 vector<int>lv[1005],rv[1005]; 7 int n,x[505],rk[505][505],Rcnt[1005],Lcnt[1005],tem[505],dp[505][505][2]; 8 void merge_sort(int l,int r){ 9 if(l==r)return; int M=l+r>>1; 10 merge_sort(l,M); merge_sort(M+1,r); 11 for(int i=l;i<=M;++i)Lcnt[x[i]]++,lv[x[i]].push_back(i); 12 for(int i=M+1;i<=r;++i)Rcnt[x[i]]++,rv[x[i]].push_back(i); 13 for(int i=1;i<=1000;++i){ 14 for(int L=0;L<=Lcnt[i];++L)for(int R=0;R<=Rcnt[i];++R)dp[L][R][0]=dp[L][R][1]=0; 15 dp[0][0][0]=1; 16 for(int L=0;L<=Lcnt[i];++L)for(int R=0;R<=Rcnt[i];++R) 17 if(L!=Lcnt[i]&&R!=Rcnt[i]) 18 dp[L+1][R][0]=(dp[L+1][R][0]+(dp[L][R][0]+dp[L][R][1])*inv)%mod, 19 dp[L][R+1][1]=(dp[L][R+1][1]+(dp[L][R][0]+dp[L][R][1])*inv)%mod; 20 else if(L!=Lcnt[i])dp[L+1][R][0]=(dp[L+1][R][0]+dp[L][R][0]+dp[L][R][1])%mod; 21 else if(R!=Rcnt[i])dp[L][R+1][1]=(dp[L][R+1][1]+dp[L][R][0]+dp[L][R][1])%mod; 22 for(int j=0;j<Lcnt[i];++j){ 23 for(int k=1;k<=Lcnt[i];++k)for(int rp=0;rp<=Rcnt[i];++rp) 24 tem[k+rp]=(tem[k+rp]+rk[lv[i][j]][k]*dp[k][rp][0])%mod; 25 for(int nrk=1;nrk<=Lcnt[i]+Rcnt[i];++nrk)rk[lv[i][j]][nrk]=tem[nrk],tem[nrk]=0; 26 } 27 for(int j=0;j<Rcnt[i];++j){ 28 for(int k=1;k<=Rcnt[i];++k)for(int lp=0;lp<=Lcnt[i];++lp) 29 tem[k+lp]=(tem[k+lp]+rk[rv[i][j]][k]*dp[lp][k][1])%mod; 30 for(int nrk=1;nrk<=Lcnt[i]+Rcnt[i];++nrk)rk[rv[i][j]][nrk]=tem[nrk],tem[nrk]=0; 31 } 32 lv[i].clear();rv[i].clear();Lcnt[i]=Rcnt[i]=0; 33 } 34 } 35 main(){//freopen("sort103.in","r",stdin); 36 scanf("%lld",&n); 37 for(int i=1;i<=n;++i)scanf("%lld",&x[i]); 38 for(int i=1;i<=n;++i)rk[i][1]=1; 39 merge_sort(1,n); 40 for(int i=1;i<=n;++i)Lcnt[x[i]]++; 41 for(int i=1;i<=1000;++i)Lcnt[i]+=Lcnt[i-1]; 42 for(int i=1;i<=n;++i){ 43 int ans=0; 44 for(int j=1;j<=Lcnt[x[i]]-Lcnt[x[i]-1];++j)ans=(ans+1ll*rk[i][j]*j)%mod;//,printf("%lld %lld\n",j,rk[i][j]); 45 printf("%lld ",ans+Lcnt[x[i]-1]); 46 }puts(""); 47 }
T3:Cicada拿衣服
英文题目名为什么叫naive??拿(na)衣(i)服(ve)???
看到这个题目名我还以为这道题真的很naive
其实只是比较好打,但是思路不是很好想
首先你需要打一个暴力,需要一个ST表来O(1)查询区间的那四个函数。
发现Dybala的ST表还是O(log)的。。。奉劝各位好好学学ST表。。。
highbit操作是要预处理的!!!不要现算!!!
然后最粗暴的就是枚举左右端点,check它的excited值,如果合法就区间取max。我是用线段树维护的。
到这里为止如果你不乱搞你能有36分。
然后正解的80%就已经打完了。
首先我们固定右端点,不断左移左端点。
对于OR,最多只会变化log次,即每一位从0变成1。
对于AND,最多也只会变化log次,每一位从1到0。
所以其实OR-AND只会变化2log次。
那么问题就是MIN-MAX了。MIN越来越小MAX越来越大所以MIN-MAX会越来越小。
所以在由OR-AND分割出的2log段里,每一段内部的excited值都满足单调性。
所以我们只要考虑在每一段里找到最靠左的excited值的合法位置,然后就线段树区间赋取max就好了。
然后怎么找到这2log个段呢?
用链表记录下每个段的右端点就好了,然后跳链表就可以。
因为右端点右移的时候,链表内部只会合并段而不会新增段,所以是可以用链表的。
所以代码其实只是多了一个链表,然后爆扫改成跳链表而已。
复杂度是$O(nlogn)$
这题数据很难造,所以乱搞可过。然而打正解需要优化常数不然容易T92什么的。。。
记得及时跳出不然还是$nlog^2$。。。我就是hanpi

1 #include<bits/stdc++.h> 2 using namespace std; 3 int mx[20][1000005],mn[20][1000005],Or[20][1000005],And[20][1000005]; 4 int ans[1000005],n,x[1000005],hi[1000005],k,t[4000005],cl[4000005],cr[4000005]; 5 int lst[1000005],nxt[1000005]; 6 void del(int p){lst[nxt[p]]=lst[p];nxt[lst[p]]=nxt[p];} 7 const int N=1e6+10; 8 const int Ls=1<<23|1; 9 char buffer[Ls],*Ss,*Ts; 10 #define getchar() ((Ss==Ts&&(Ts=(Ss=buffer)+fread(buffer,1,Ls,stdin),Ss==Ts))?EOF:*Ss++) 11 int read(register int p=0,register char ch=getchar()){ 12 while(ch<'0'||ch>'9')ch=getchar(); 13 while(ch>='0'&&ch<='9')p=(p<<3)+(p<<1)+ch-'0',ch=getchar(); 14 return p; 15 } 16 #define Max(a,b) ((a)>(b)?(a):(b)) 17 #define Min(a,b) ((a)<(b)?(a):(b)) 18 int _max(int l,int r){ 19 int x=hi[r-l+1]; 20 return Max(mx[x][l],mx[x][r-(1<<x)+1]); 21 } 22 int _min(int l,int r){ 23 int x=hi[r-l+1]; 24 return Min(mn[x][l],mn[x][r-(1<<x)+1]); 25 } 26 int _or(int l,int r){ 27 int x=hi[r-l+1]; 28 return Or[x][l]|Or[x][r-(1<<x)+1]; 29 } 30 int _and(int l,int r){ 31 int x=hi[r-l+1]; 32 return And[x][l]&And[x][r-(1<<x)+1]; 33 } 34 int excited(int l,int r){ 35 return _or(l,r)-_max(l,r)+_min(l,r)-_and(l,r); 36 } 37 void build(int p,int l,int r){ 38 cl[p]=l;cr[p]=r;t[p]=-1; 39 if(l==r)return; 40 build(p<<1,l,l+r>>1); 41 build(p<<1|1,(l+r>>1)+1,r); 42 } 43 void modify(int p,int l,int r,int w){ 44 if(l<=cl[p]&&cr[p]<=r)return t[p]=Max(t[p],w),(void)0; 45 if(l<=cr[p<<1]) modify(p<<1,l,r,w); 46 if(r>cr[p<<1]) modify(p<<1|1,l,r,w); 47 } 48 void dfs(int p,int w){ 49 w=Max(w,t[p]); 50 if(cl[p]==cr[p])return printf("%d ",w),(void)0; 51 dfs(p<<1,w); dfs(p<<1|1,w); 52 } 53 int chk(int l,int r,int R){ 54 while(l<r-1)if(excited(l+r>>1,R)>=k)r=l+r>>1;else l=(l+r>>1)+1; 55 if(excited(l,R)>=k)return l;return r; 56 } 57 int main(){//freopen("naive105.in","r",stdin);freopen("my.out","w",stdout); 58 scanf("%d%d",&n,&k);build(1,1,n); 59 for(int i=1;i<=n;++i)x[i]=read(),lst[i]=i-1,nxt[i]=i+1; 60 nxt[0]=1; 61 for(int i=1;i<=n;++i) mx[0][i]=mn[0][i]=Or[0][i]=And[0][i]=x[i]; 62 for(int j=1;j<20;++j)for(int i=1;i+(1<<j)-1<=n;++i) 63 mx[j][i]=Max(mx[j-1][i],mx[j-1][i+(1<<j-1)]), 64 mn[j][i]=Min(mn[j-1][i],mn[j-1][i+(1<<j-1)]), 65 Or[j][i]=Or[j-1][i]|Or[j-1][i+(1<<j-1)], 66 And[j][i]=And[j-1][i]&And[j-1][i+(1<<j-1)]; 67 for(int j=0;j<20;++j)for(int i=1<<j;i<1<<j+1&&i<=n;++i)hi[i]=j; 68 for(int r=1;r<=n;++r){ 69 for(int i=lst[r];i;i=lst[i])if(_or(nxt[i],r)==_or(i,r)&&_and(nxt[i],r)==_and(i,r))del(i); 70 for(int i=nxt[0],p;i<=r;i=nxt[i])if(excited(i,r)>=k){p=chk(lst[i]+1,i,r),modify(1,p,r,r-p+1);break;} 71 } 72 dfs(1,-1);puts(""); 73 }



