[ bzoj2820] YY的GCD

[ bzoj2820] YY的GCD

Time Limit : 3000 ms

Description

神犇YY虐完数论后给傻×kAc出了一题给定N, M,求1<=x<=N, 1<=y<=M且gcd(x, y)为质数的(x, y)有多少对kAc这种傻×必然不会了，于是向你来请教……

多组输入

Input

第一行一个整数T 表述数据组数接下来T行，每行两个正整数，表示N, M

Output

T行，每行一个整数表示第i组数据的结果

Sample Input

2

10 10

100 100

Sample Output

30

2791

Hint

T = 10000    N, M <= 10000000

前置知识：

　　莫比乌斯函数，莫比乌斯反演，欧拉线性筛，数论分块（分段），约数个数

　　大概说一说吧我也是第一次做这种题，会的跳过直接进正题

　　　　莫比乌斯函数：k分解质因数为a₁^b₁a₂^b₂...a_m^b_m  (a₁,a₂...a_m为彼此不同的质数)

　　　　　　　　　　　　若b₁,b₂...b_n中有大于1的项，则μ(k)=0

　　　　　　　　　　　　否则μ(k)=(-1)^m

 

　　　　莫比乌斯反演：对于已知函数f和g，若满足

　　　　　　　　　　　　　　f(n)=Σ g(d)  (其中d是n的约数)

　　　　　　　　　　　　则有
　　　　　　　　　　　　　　g(n)=Σ μ(d)*f(n/d) (其中d是n的约数)

　　　　　　　　　　　　常见形式为Σ μ(d)= [n] (其中d是n的约数，[n]等同于代码中的（n==1?1:0）)

　　　　欧拉线性筛：可以在线性复杂度内求出素数，欧拉函数，莫比乌斯函数，详见代码

 

　　　　约数个数：n的约数最多只有2√n个。

　　　　　　　　　　对于一个约数a，p/a也是它的约数，除恰好为√n外成对存在。

　　　　　　　　　　如果a<√n，那么p/a>√n。小于√n的显然最多有√n个，那么最多就有√n对即2√n个。

 

　　　　数论分块:求和Σ时,随着参数递增而函数值变化频率很低时,直接求每个函数值的出现次数×函数值。

　　　　　　　　　　如：给出k，求Σ(k/i) (/为整除，i<=k)。

　　　　　　　　　　k=135时，只要68<=i<=135，(k/i)就是1，每次都除显然浪费时间，故求出68与135这两个端点，乘以(k/i)的值1即可。

　　　　　　　　　　　　结合约数个数那一条，这个问题可以从O(n)降低为O(2√n)求解

正题：

话说这个题目名竟然没有被和谐

首先，并不难列出最基础的式子：

其中p为质数，那么我们可以通过枚举质数来求解，假设n<=m，否则swap。

将p提出，同时x和y的含义发生变化，变为（是p的几倍），这样x和y的枚举上界就缩小了p倍。

根据莫比乌斯反演：Σ μ(d)= [n] (其中d是n的约数，[n]等同于代码中的（n==1?1:0）)

x和y能整除gcd(x,y)，而gcd(x,y)能整除d，则x和y都能整除d。

改变枚举顺序，先枚举d,那么x，y都是d的倍数，则再次改变x,y的含义(pd的倍数)。

d的范围自然是min(n/p,m/p),这样就可以把μ(d)提到外层。

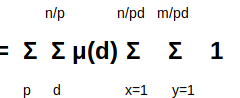
里面两层的Σ的累加值既然是1，那么就是枚举几次就是几咯(|_ a_|表示a向下取整)

可以发现Σ后面的式子与p*d关联挺大，所以转换思路枚举k=p*d

(不要问我是怎么想到的，不然我也不会是一个在这里写博客的蒟蒻了)

(从这个式子往下省略下取整符号，我太弱了找不到它！所有除号都表示整除，为了方便区分加上了括号)

其中(n/k)*(m/k)项与p无关，可以提出来。

看起来好像化简到头了，为了放松放松脑子，我们先不推公式了，我们来初始化它。

Σ μ(k/p)只与k有关而与m，n无关，可以预处理出来，设它是f(k)=Σ μ(k/p),其中p是小于等于k的质数。

看起来通过枚举k及k以下的p，复杂度是O(n²)级别，难以接受。

转换思路，k不能枚举那就枚举p呗。

通过枚举每个质数p，累加对其他数的贡献，实际复杂度会下降不少。

讲不明白，上代码，还是直接颓代码比较直接痛快。

for(int i=1,j=prime[1];i<=nop;j=prime[++i])
        for(int k=j;k<=maxn;k+=j)
            f[k]+=miu[k/j];

实际复杂度是O(n log n),可以接受。

 那么f函数就搞定了，原算式更简单了。

 这样我们就可以O(n)处理每个询问了，可是面对数据范围还是只有部分分。

内心：就这样算了，考场上肯定就码暴力了。

不行，不屈的衡中学子我们要追求卓越。

我们可以发现当k趋近于n时，(n/k)与(m/k)两项变化很慢,k增大1时这两项很可能都不变,考虑分段处理。

而每次都在变化的f(k),我们可以用前缀和来求区间和,存在totf里，即totf(k)=Σf(i)   (i<=k)

(n/k)最多2√n段，(m/k)也是这个级别，所以一共最多4√n段。

每次询问的复杂度为√n级别，可以接受。

呼，完成啦！

最终10个测试点8900ms，比较充裕。

附码量很小（脑量很大）的AC代码。

ps：分段那部分打麻烦了，其实码量可以更小，详见其他神犇

（我这个蒟蒻总不能比他们打的好吧，其实是我故意的）

ps：本人码风自带防抄，对拍等等可以，提交请谨慎。

#include<cstdio>
#include<cmath>
using namespace std;
const int maxn=1e7;
int prime[maxn],notprime[maxn+5],nop,n,m,miu[maxn+5],t,enda[6666],endb[6666],ca[6666],cb[6666],sda,sdb,sqr;long long f[maxn+5],qz[maxn+5],ans;
int main(){
    for(int i=1;i<=maxn;++i)miu[i]=1;
    for(int i=2;i<=maxn;++i){
        if(!notprime[i]){nop++;prime[nop]=i;miu[i]=-1;}
        for(int j=1;j<=nop&&i*prime[j]<=maxn;++j){
            notprime[i*prime[j]]=1;
            if(i%prime[j]){miu[i*prime[j]]=-miu[i];continue;}
            miu[i*prime[j]]=0;
            break;
        }
    }
    for(int i=1,j=prime[1];i<=nop;j=prime[++i])
        for(int k=j;k<=maxn;k+=j)
            f[k]+=miu[k/j];
    for(int i=1;i<=maxn;++i)qz[i]=qz[i-1]+f[i];
    scanf("%d",&t);
    while(t--){
        scanf("%d%d",&m,&n);sda=0;sdb=0;if(m>n)sqr=m,m=n,n=sqr;
        sqr=sqrt(n);ans=0;
        for(int i=1;i<=sqr;++i)ca[++sda]=n/i,enda[sda]=i;
        for(int i=sqr;i;--i)ca[++sda]=i,enda[sda]=n/i;
        sqr=sqrt(m);
        for(int i=1;i<=sqr;++i)cb[++sdb]=m/i,endb[sdb]=i;
        for(int i=sqr;i;--i)cb[++sdb]=i,endb[sdb]=m/i;
        while(enda[sda-1]>=m)sda--;enda[sda]=sqr=m;
        while(sda&&sdb){
            if(enda[sda-1]==endb[sdb-1])ans+=(qz[sqr]-qz[endb[sdb-1]])*ca[sda]*cb[sdb],sqr=endb[sdb-1],sdb--,sda--;
            else if(enda[sda-1]<endb[sdb-1])ans+=(qz[sqr]-qz[endb[sdb-1]])*ca[sda]*cb[sdb],sqr=endb[sdb-1],sdb--;
            else ans+=(qz[sqr]-qz[enda[sda-1]])*ca[sda]*cb[sdb],sqr=enda[sda-1],sda--;
        }
        printf("%lld\n",ans);
    }
}

 update 6/13:依据Dybala_zdy大神的优化.

先读入全部询问，根据其最大值确定线性筛等预处理的范围，优化至5700ms。

#include<cstdio>
#include<cmath>
using namespace std;
#define maxnnn 10000000
inline int max(int a,int b){return a>b?a:b;}
int maxn=0,tm[10005],tn[10005];
int prime[maxnnn],notprime[maxnnn+5],nop,n,m,miu[maxnnn+5],t,enda[6666],endb[6666],ca[6666],cb[6666],sda,sdb,sqr;long long f[maxnnn+5],qz[maxnnn+5],ans;
int main(){scanf("%d",&t);
    for(int i=1;i<=t;++i){
        scanf("%d%d",&tm[i],&tn[i]);
        maxn=max(maxn,max(tm[i],tn[i]));
    }
    for(int i=1;i<=maxn;++i)miu[i]=1;
    for(int i=2;i<=maxn;++i){
        if(!notprime[i]){nop++;prime[nop]=i;miu[i]=-1;}
        for(int j=1;j<=nop&&i*prime[j]<=maxn;++j){
            notprime[i*prime[j]]=1;
            if(i%prime[j]){miu[i*prime[j]]=-miu[i];continue;}
            miu[i*prime[j]]=0;
            break;
        }
    }
    for(int i=1,j=prime[1];i<=nop;j=prime[++i])
        for(int k=j;k<=maxn;k+=j)
            f[k]+=miu[k/j];
    for(int i=1;i<=maxn;++i)qz[i]=qz[i-1]+f[i];
    for(int ii=1;ii<=t;++ii){
        m=tm[ii];n=tn[ii];sda=0;sdb=0;if(m>n)sqr=m,m=n,n=sqr;
        sqr=sqrt(n);ans=0;
        for(int i=1;i<=sqr;++i)ca[++sda]=n/i,enda[sda]=i;
        for(int i=sqr;i;--i)ca[++sda]=i,enda[sda]=n/i;
        sqr=sqrt(m);
        for(int i=1;i<=sqr;++i)cb[++sdb]=m/i,endb[sdb]=i;
        for(int i=sqr;i;--i)cb[++sdb]=i,endb[sdb]=m/i;
        while(enda[sda-1]>=m)sda--;enda[sda]=sqr=m;
        while(sda&&sdb){
            if(enda[sda-1]==endb[sdb-1])ans+=(qz[sqr]-qz[endb[sdb-1]])*ca[sda]*cb[sdb],sqr=endb[sdb-1],sdb--,sda--;
            else if(enda[sda-1]<endb[sdb-1])ans+=(qz[sqr]-qz[endb[sdb-1]])*ca[sda]*cb[sdb],sqr=endb[sdb-1],sdb--;
            else ans+=(qz[sqr]-qz[enda[sda-1]])*ca[sda]*cb[sdb],sqr=enda[sda-1],sda--;
        }
        printf("%lld\n",ans);
    }
}