2024.11.5 闲话

别人的闲话都推图or歌，我的鲜花啥也没有。我也没啥可推的啊，求图or歌

高维前缀和

常见的柿子是\(s_{i,j} = s_{i-1,j} + s_{i,j-1}-s_{i-1,j-1}+a_{i,j}\)。

但是还可以一维一维求。

点此查看代码

rep(i,1,n,1) rep(j,1,m,1) a[i][j] += a[i-1][j];
rep(i,1,n,1) rep(j,1,m,1) a[i][j] += a[i][j-1];

三维同理，高维也是一样的套路，时间复杂度\(O(\text{维度}\times n^{\text{维度}})\)。

SOSDP

考虑这道题。

给定一个长度为\(2^n\)的数组\(a\)，定义\(f_{i}=\sum\limits_{j\And i=i}a_j\)，\(\forall i\in [1,n]\)，求\(f_i\)

一个显然的暴力就是枚举\(i,j\)，时间复杂度\(O(4^n)\)。再一个显然的暴力是对于每一个\(i\)，枚举子集，时间复杂度\(O(\sum_{k=0}^n2^k)=O(3^n)\)。

如何枚举二进制子集

令\(t=s\)，然后不断令\(t=(t-1)\And s\)，即可枚举\(s\)的所有子集。

证明的话可以自己模拟理解一下或者bdfs。

但是如果\(n\le 20\)，那么上面两种方法就似了。现在考虑如何优化\(3^n\)的暴力。发现这个暴力的缺陷是当一个状态的二进制位上有\(k\)个\(0\)的时候，它会被访问\(2^k-1\)次，这是非常不优秀的。

定义集合\(S(sta)=\{x|x\subseteq sta\}\)，然后定义\(S(sta,i)=\{x|x\subseteq sta \And\And sta\oplus x < 2^{i+1}\}\)

看起来可能很不好理解，说人话就是只有第\(i\)及以后位与\(sta\)不同的\(x\)的集合（注意此处是从0开始）。例如\(S(\)1011010,3\()=\{\)1011010,1011000,1010010,1010000\(\}\)。

尝试将\(sta\)与\(x\)联系，根据\(sta\)的第\(i\)位数，分情况讨论。

• 第\(i\)位为\(0\)

  那么显然有\(S(sta,i)=S(sta,i-1)\)

• 第\(i\)位为\(1\)

  还是要按照\(x\)的第\(i\)位的数分两种

  • 为\(0\)，那么就是\(S(sta\oplus 2^i,i-1)\)
  • 为\(1\)，那么就是\(S(sta,i-1)\)

  所以\(S(sta,i)=S(sta,i-1)+S(sta\oplus 2^i,i-1)\)

画出图来大概就是这样的东西，其中红色前缀表示这一部分是公共的，而黑色部分允许不同。

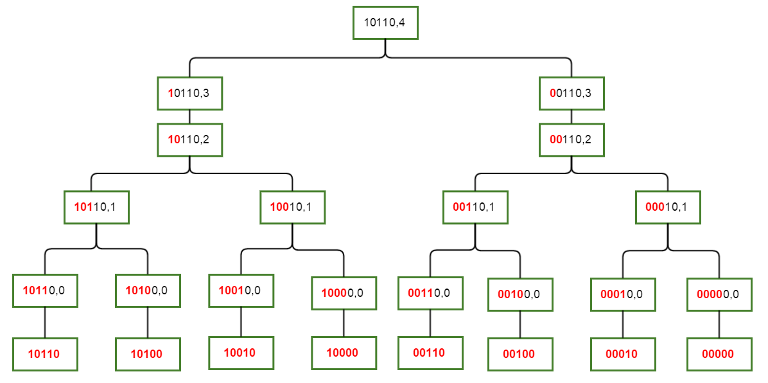
容易发现这是个\(DAG\)。（你可能会认为这是个有根树，这是错误的，考虑当\(sta\)不同但\(i\)相同时，可能有一个点有两个及以上前驱）然后就可以直接根据这个跑dp了。

点此查看代码

rep(i,0,(1<<n)-1,1) f[i] = a[i];
rep(i,0,n-1,1) rep(j,0,(1<<n)-1,1) if(j&(1<<i)) f[i] += f[i^(1<<j)];

其实这玩意还可以求超集和。

超集是(cjs)什么

定义：如果一个集合S2中的每一个元素都在集合S1中，且集合S1中可能包含S2中没有的元素，则集合S1就是S2的一个超集，反过来，S2是S1的子集。 S1是S2的超集，若S1中一定有S2中没有的元素，则S1是S2的真超集，反过来S2是S1的真子集。

其实核心代码差不多

点此查看代码

rep(i,0,(1<<n)-1,1) f[i] = a[i];
rep(i,0,n-1,1) drep(j,(1<<n)-1,0,1) if(!(j&(1<<i))) f[i] += f[i^(1<<j)];

感性理解一下，就是把二进制中的\(0,1\)反过来看。

\(but\)，到现在为止，还没说这玩意和高维前缀和有什么关系。

其实非常简单，看\(f_{i}=f_{i}+f_{i\oplus (1<<j)}\)，这个就是一个前缀和。

题单